Uniform Risk Bounds for Learning with Dependent Data Sequences

This paper extends standard results from learning theory with independent data to sequences of dependent data. Contrary to most of the literature, we do not rely on mixing arguments or sequential measures of complexity and derive uniform risk bounds with classical proof patterns and capacity measures. In particular, we show that the standard classification risk bounds based on the VC-dimension hold in the exact same form for dependent data, and further provide Rademacher complexity-based bounds, that remain unchanged compared to the standard results for the identically and independently distributed case. Finally, we show how to apply these results in the context of scenario-based optimization in order to compute the sample complexity of random programs with dependent constraints.

Margin theory for the scenario-based approach to robust optimization in high dimension

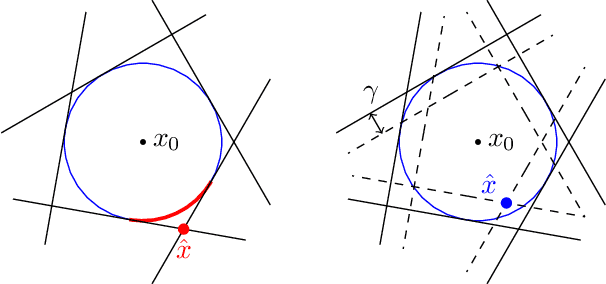
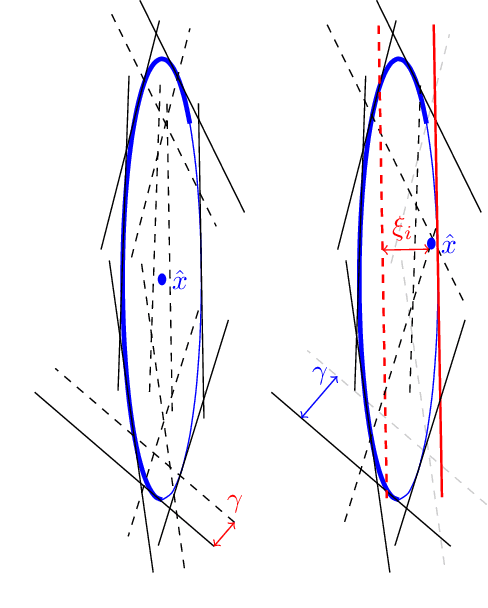
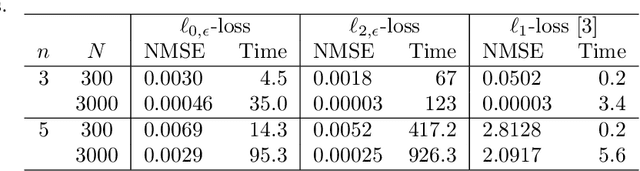
This paper deals with the scenario approach to robust optimization. This relies on a random sampling of the possibly infinite number of constraints induced by uncertainties in the parameters of an optimization problem. Solving the resulting random program yields a solution for which the quality is measured in terms of the probability of violating the constraints for a random value of the uncertainties, typically unseen before. Another central issue is the determination of the sample complexity, i.e., the number of random constraints (or scenarios) that one must consider in order to guarantee a certain level of reliability. In this paper, we introduce the notion of margin to improve upon standard results in this field. In particular, using tools from statistical learning theory, we show that the sample complexity of a class of random programs does not explicitly depend on the number of variables. In addition, within the considered class, that includes polynomial constraints among others, this result holds for both convex and nonconvex instances with the same level of guarantees. We also derive a posteriori bounds on the probability of violation and sketch a regularization approach that could be used to improve the reliability of computed solutions on the basis of these bounds.

Risk Bounds for Learning Multiple Components with Permutation-Invariant Losses

This paper proposes a simple approach to derive efficient error bounds for learning multiple components with sparsity-inducing regularization. Indeed, we show that for such regularization schemes, known decompositions of the Rademacher complexity over the components can be used in a more efficient manner to result in tighter bounds without too much effort. We give examples of application to switching regression and center-based clustering/vector quantization. Then, the complete workflow is illustrated on the problem of subspace clustering, for which decomposition results were not previously available. For all these problems, the proposed approach yields risk bounds with mild dependencies on the number of components and completely removes this dependency for nonconvex regularization schemes that could not be handled by previous methods.

Rademacher Complexity and Generalization Performance of Multi-category Margin Classifiers

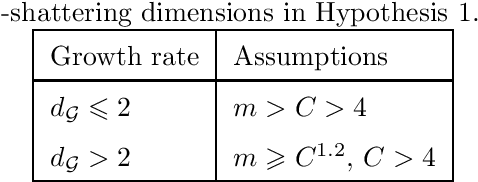
One of the main open problems in the theory of multi-category margin classification is the form of the optimal dependency of a guaranteed risk on the number C of categories, the sample size m and the margin parameter gamma. From a practical point of view, the theoretical analysis of generalization performance contributes to the development of new learning algorithms. In this paper, we focus only on the theoretical aspect of the question posed. More precisely, under minimal learnability assumptions, we derive a new risk bound for multi-category margin classifiers. We improve the dependency on C over the state of the art when the margin loss function considered satisfies the Lipschitz condition. We start with the basic supremum inequality that involves a Rademacher complexity as a capacity measure. This capacity measure is then linked to the metric entropy through the chaining method. In this context, our improvement is based on the introduction of a new combinatorial metric entropy bound.

On the exact minimization of saturated loss functions for robust regression and subspace estimation

This paper deals with robust regression and subspace estimation and more precisely with the problem of minimizing a saturated loss function. In particular, we focus on computational complexity issues and show that an exact algorithm with polynomial time-complexity with respect to the number of data can be devised for robust regression and subspace estimation. This result is obtained by adopting a classification point of view and relating the problems to the search for a linear model that can approximate the maximal number of points with a given error. Approximate variants of the algorithms based on ramdom sampling are also discussed and experiments show that it offers an accuracy gain over the traditional RANSAC for a similar algorithmic simplicity.

Error Bounds for Piecewise Smooth and Switching Regression

The paper deals with regression problems, in which the nonsmooth target is assumed to switch between different operating modes. Specifically, piecewise smooth (PWS) regression considers target functions switching deterministically via a partition of the input space, while switching regression considers arbitrary switching laws. The paper derives generalization error bounds in these two settings by following the approach based on Rademacher complexities. For PWS regression, our derivation involves a chaining argument and a decomposition of the covering numbers of PWS classes in terms of the ones of their component functions and the capacity of the classifier partitioning the input space. This yields error bounds with a radical dependency on the number of modes. For switching regression, the decomposition can be performed directly at the level of the Rademacher complexities, which yields bounds with a linear dependency on the number of modes. By using once more chaining and a decomposition at the level of covering numbers, we show how to recover a radical dependency. Examples of applications are given in particular for PWS and swichting regression with linear and kernel-based component functions.

Global optimization for low-dimensional switching linear regression and bounded-error estimation

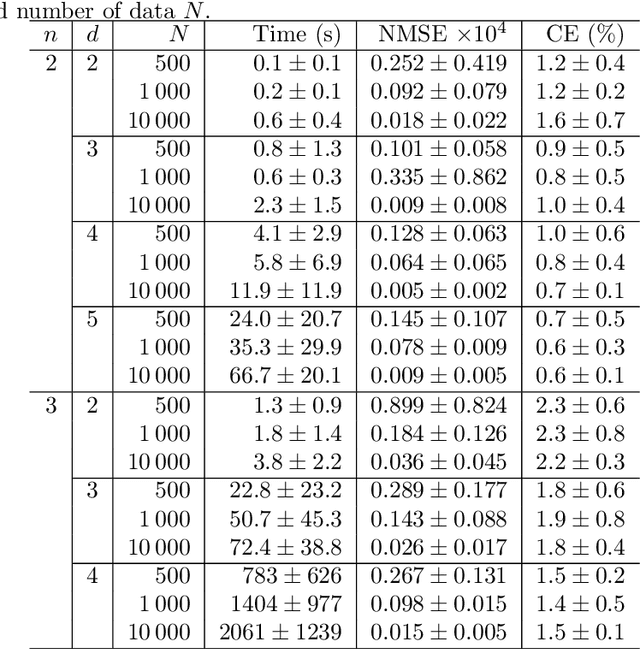
The paper provides global optimization algorithms for two particularly difficult nonconvex problems raised by hybrid system identification: switching linear regression and bounded-error estimation. While most works focus on local optimization heuristics without global optimality guarantees or with guarantees valid only under restrictive conditions, the proposed approach always yields a solution with a certificate of global optimality. This approach relies on a branch-and-bound strategy for which we devise lower bounds that can be efficiently computed. In order to obtain scalable algorithms with respect to the number of data, we directly optimize the model parameters in a continuous optimization setting without involving integer variables. Numerical experiments show that the proposed algorithms offer a higher accuracy than convex relaxations with a reasonable computational burden for hybrid system identification. In addition, we discuss how bounded-error estimation is related to robust estimation in the presence of outliers and exact recovery under sparse noise, for which we also obtain promising numerical results.

On the complexity of switching linear regression

This technical note extends recent results on the computational complexity of globally minimizing the error of piecewise-affine models to the related problem of minimizing the error of switching linear regression models. In particular, we show that, on the one hand the problem is NP-hard, but on the other hand, it admits a polynomial-time algorithm with respect to the number of data points for any fixed data dimension and number of modes.

On the complexity of piecewise affine system identification

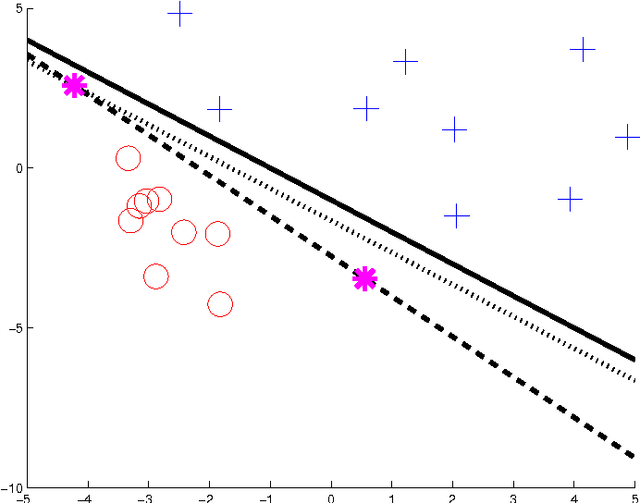
The paper provides results regarding the computational complexity of hybrid system identification. More precisely, we focus on the estimation of piecewise affine (PWA) maps from input-output data and analyze the complexity of computing a global minimizer of the error. Previous work showed that a global solution could be obtained for continuous PWA maps with a worst-case complexity exponential in the number of data. In this paper, we show how global optimality can be reached for a slightly more general class of possibly discontinuous PWA maps with a complexity only polynomial in the number of data, however with an exponential complexity with respect to the data dimension. This result is obtained via an analysis of the intrinsic classification subproblem of associating the data points to the different modes. In addition, we prove that the problem is NP-hard, and thus that the exponential complexity in the dimension is a natural expectation for any exact algorithm.

Finding sparse solutions of systems of polynomial equations via group-sparsity optimization

The paper deals with the problem of finding sparse solutions to systems of polynomial equations possibly perturbed by noise. In particular, we show how these solutions can be recovered from group-sparse solutions of a derived system of linear equations. Then, two approaches are considered to find these group-sparse solutions. The first one is based on a convex relaxation resulting in a second-order cone programming formulation which can benefit from efficient reweighting techniques for sparsity enhancement. For this approach, sufficient conditions for the exact recovery of the sparsest solution to the polynomial system are derived in the noiseless setting, while stable recovery results are obtained for the noisy case. Though lacking a similar analysis, the second approach provides a more computationally efficient algorithm based on a greedy strategy adding the groups one-by-one. With respect to previous work, the proposed methods recover the sparsest solution in a very short computing time while remaining at least as accurate in terms of the probability of success. This probability is empirically analyzed to emphasize the relationship between the ability of the methods to solve the polynomial system and the sparsity of the solution.