Generalization Bounds for Inductive Matrix Completion in Low-noise Settings

We study inductive matrix completion (matrix completion with side information) under an i.i.d. subgaussian noise assumption at a low noise regime, with uniform sampling of the entries. We obtain for the first time generalization bounds with the following three properties: (1) they scale like the standard deviation of the noise and in particular approach zero in the exact recovery case; (2) even in the presence of noise, they converge to zero when the sample size approaches infinity; and (3) for a fixed dimension of the side information, they only have a logarithmic dependence on the size of the matrix. Differently from many works in approximate recovery, we present results both for bounded Lipschitz losses and for the absolute loss, with the latter relying on Talagrand-type inequalities. The proofs create a bridge between two approaches to the theoretical analysis of matrix completion, since they consist in a combination of techniques from both the exact recovery literature and the approximate recovery literature.

Rademacher Complexity and Generalization Performance of Multi-category Margin Classifiers

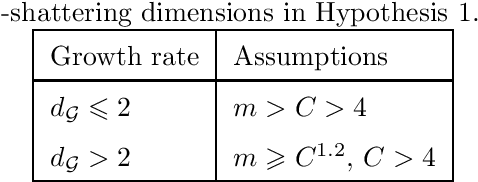
One of the main open problems in the theory of multi-category margin classification is the form of the optimal dependency of a guaranteed risk on the number C of categories, the sample size m and the margin parameter gamma. From a practical point of view, the theoretical analysis of generalization performance contributes to the development of new learning algorithms. In this paper, we focus only on the theoretical aspect of the question posed. More precisely, under minimal learnability assumptions, we derive a new risk bound for multi-category margin classifiers. We improve the dependency on C over the state of the art when the margin loss function considered satisfies the Lipschitz condition. We start with the basic supremum inequality that involves a Rademacher complexity as a capacity measure. This capacity measure is then linked to the metric entropy through the chaining method. In this context, our improvement is based on the introduction of a new combinatorial metric entropy bound.

Combinatorial and Structural Results for gamma-Psi-dimensions

One of the main open problems of the theory of margin multi-category pattern classification is the characterization of the way the confidence interval of a guaranteed risk should vary as a function of the three basic parameters which are the sample size m, the number C of categories and the scale parameter gamma. This is especially the case when working under minimal learnability hypotheses. In that context, the derivation of a bound is based on the handling of capacity measures belonging to three main families: Rademacher/Gaussian complexities, metric entropies and scale-sensitive combinatorial dimensions. The scale-sensitive combinatorial dimensions dedicated to the classifiers of interest are the gamma-Psi-dimensions. This article introduces the combinatorial and structural results needed to involve them in the derivation of guaranteed risks. Such a bound is then established, under minimal hypotheses regarding the classifier. Its dependence on m, C and gamma is characterized. The special case of multi-class support vector machines is used to illustrate the capacity of the gamma-Psi-dimensions to take into account the specificities of a classifier.

A Quadratic Loss Multi-Class SVM

Using a support vector machine requires to set two types of hyperparameters: the soft margin parameter C and the parameters of the kernel. To perform this model selection task, the method of choice is cross-validation. Its leave-one-out variant is known to produce an estimator of the generalization error which is almost unbiased. Its major drawback rests in its time requirement. To overcome this difficulty, several upper bounds on the leave-one-out error of the pattern recognition SVM have been derived. Among those bounds, the most popular one is probably the radius-margin bound. It applies to the hard margin pattern recognition SVM, and by extension to the 2-norm SVM. In this report, we introduce a quadratic loss M-SVM, the M-SVM^2, as a direct extension of the 2-norm SVM to the multi-class case. For this machine, a generalized radius-margin bound is then established.

Scale-sensitive Psi-dimensions: the Capacity Measures for Classifiers Taking Values in R^Q

Bounds on the risk play a crucial role in statistical learning theory. They usually involve as capacity measure of the model studied the VC dimension or one of its extensions. In classification, such "VC dimensions" exist for models taking values in {0, 1}, {1,..., Q} and R. We introduce the generalizations appropriate for the missing case, the one of models with values in R^Q. This provides us with a new guaranteed risk for M-SVMs which appears superior to the existing one.