Shared active subspace for multivariate vector-valued functions

This paper proposes several approaches as baselines to compute a shared active subspace for multivariate vector-valued functions. The goal is to minimize the deviation between the function evaluations on the original space and those on the reconstructed one. This is done either by manipulating the gradients or the symmetric positive (semi-)definite (SPD) matrices computed from the gradients of each component function so as to get a single structure common to all component functions. These approaches can be applied to any data irrespective of the underlying distribution unlike the existing vector-valued approach that is constrained to a normal distribution. We test the effectiveness of these methods on five optimization problems. The experiments show that, in general, the SPD-level methods are superior to the gradient-level ones, and are close to the vector-valued approach in the case of a normal distribution. Interestingly, in most cases it suffices to take the sum of the SPD matrices to identify the best shared active subspace.

Sample Complexity Result for Multi-category Classifiers of Bounded Variation

We control the probability of the uniform deviation between empirical and generalization performances of multi-category classifiers by an empirical L1 -norm covering number when these performances are defined on the basis of the truncated hinge loss function. The only assumption made on the functions implemented by multi-category classifiers is that they are of bounded variation (BV). For such classifiers, we derive the sample size estimate sufficient for the mentioned performances to be close with high probability. Particularly, we are interested in the dependency of this estimate on the number C of classes. To this end, first, we upper bound the scale-sensitive version of the VC-dimension, the fat-shattering dimension of sets of BV functions defined on R^d which gives a O(1/epsilon^d ) as the scale epsilon goes to zero. Secondly, we provide a sharper decomposition result for the fat-shattering dimension in terms of C, which for sets of BV functions gives an improvement from O(C^(d/2 +1)) to O(Cln^2(C)). This improvement then propagates to the sample complexity estimate.

Rademacher Complexity and Generalization Performance of Multi-category Margin Classifiers

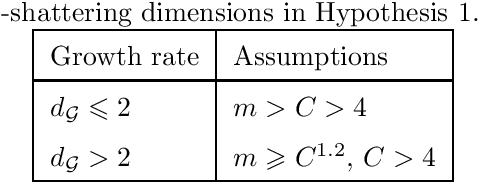
One of the main open problems in the theory of multi-category margin classification is the form of the optimal dependency of a guaranteed risk on the number C of categories, the sample size m and the margin parameter gamma. From a practical point of view, the theoretical analysis of generalization performance contributes to the development of new learning algorithms. In this paper, we focus only on the theoretical aspect of the question posed. More precisely, under minimal learnability assumptions, we derive a new risk bound for multi-category margin classifiers. We improve the dependency on C over the state of the art when the margin loss function considered satisfies the Lipschitz condition. We start with the basic supremum inequality that involves a Rademacher complexity as a capacity measure. This capacity measure is then linked to the metric entropy through the chaining method. In this context, our improvement is based on the introduction of a new combinatorial metric entropy bound.