Adaptive Replication Strategies in Trust-Region-Based Bayesian Optimization of Stochastic Functions

We develop and analyze a method for stochastic simulation optimization relying on Gaussian process models within a trust-region framework. We are interested in the case when the variance of the objective function is large. We propose to rely on replication and local modeling to cope with this high-throughput regime, where the number of evaluations may become large to get accurate results while still keeping good performance. We propose several schemes to encourage replication, from the choice of the acquisition function to setup evaluation costs. Compared with existing methods, our results indicate good scaling, in terms of both accuracy (several orders of magnitude better than existing methods) and speed (taking into account evaluation costs).

Gearing Gaussian process modeling and sequential design towards stochastic simulators

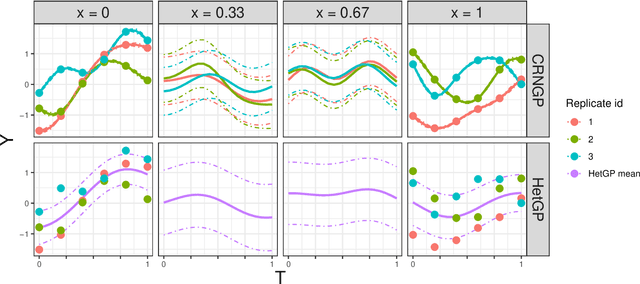
This chapter presents specific aspects of Gaussian process modeling in the presence of complex noise. Starting from the standard homoscedastic model, various generalizations from the literature are presented: input varying noise variance, non-Gaussian noise, or quantile modeling. These approaches are compared in terms of goal, data availability and inference procedure. A distinction is made between methods depending on their handling of repeated observations at the same location, also called replication. The chapter concludes with the corresponding adaptations of the sequential design procedures. These are illustrated in an example from epidemiology.

Combining additivity and active subspaces for high-dimensional Gaussian process modeling

Gaussian processes are a widely embraced technique for regression and classification due to their good prediction accuracy, analytical tractability and built-in capabilities for uncertainty quantification. However, they suffer from the curse of dimensionality whenever the number of variables increases. This challenge is generally addressed by assuming additional structure in theproblem, the preferred options being either additivity or low intrinsic dimensionality. Our contribution for high-dimensional Gaussian process modeling is to combine them with a multi-fidelity strategy, showcasing the advantages through experiments on synthetic functions and datasets.

Shared active subspace for multivariate vector-valued functions

This paper proposes several approaches as baselines to compute a shared active subspace for multivariate vector-valued functions. The goal is to minimize the deviation between the function evaluations on the original space and those on the reconstructed one. This is done either by manipulating the gradients or the symmetric positive (semi-)definite (SPD) matrices computed from the gradients of each component function so as to get a single structure common to all component functions. These approaches can be applied to any data irrespective of the underlying distribution unlike the existing vector-valued approach that is constrained to a normal distribution. We test the effectiveness of these methods on five optimization problems. The experiments show that, in general, the SPD-level methods are superior to the gradient-level ones, and are close to the vector-valued approach in the case of a normal distribution. Interestingly, in most cases it suffices to take the sum of the SPD matrices to identify the best shared active subspace.

Trajectory-oriented optimization of stochastic epidemiological models

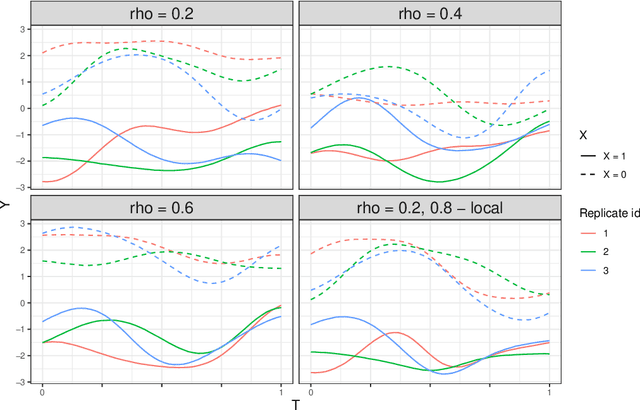
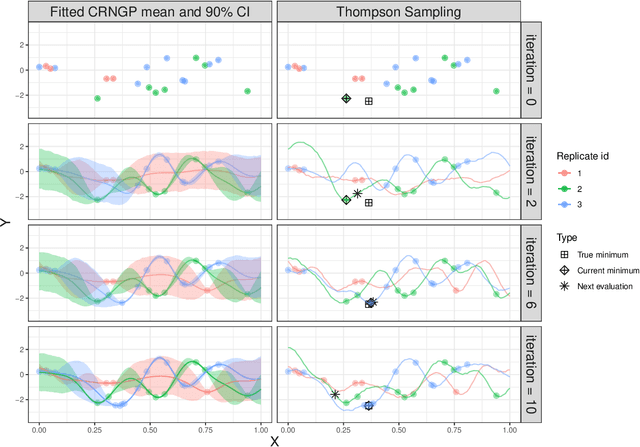
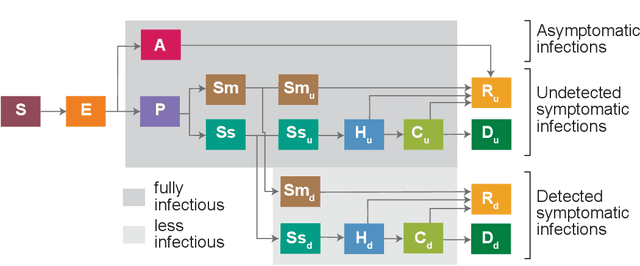
Epidemiological models must be calibrated to ground truth for downstream tasks such as producing forward projections or running what-if scenarios. The meaning of calibration changes in case of a stochastic model since output from such a model is generally described via an ensemble or a distribution. Each member of the ensemble is usually mapped to a random number seed (explicitly or implicitly). With the goal of finding not only the input parameter settings but also the random seeds that are consistent with the ground truth, we propose a class of Gaussian process (GP) surrogates along with an optimization strategy based on Thompson sampling. This Trajectory Oriented Optimization (TOO) approach produces actual trajectories close to the empirical observations instead of a set of parameter settings where only the mean simulation behavior matches with the ground truth.

A portfolio approach to massively parallel Bayesian optimization

One way to reduce the time of conducting optimization studies is to evaluate designs in parallel rather than just one-at-a-time. For expensive-to-evaluate black-boxes, batch versions of Bayesian optimization have been proposed. They work by building a surrogate model of the black-box that can be used to select the designs to evaluate efficiently via an infill criterion. Still, with higher levels of parallelization becoming available, the strategies that work for a few tens of parallel evaluations become limiting, in particular due to the complexity of selecting more evaluations. It is even more crucial when the black-box is noisy, necessitating more evaluations as well as repeating experiments. Here we propose a scalable strategy that can keep up with massive batching natively, focused on the exploration/exploitation trade-off and a portfolio allocation. We compare the approach with related methods on deterministic and noisy functions, for mono and multiobjective optimization tasks. These experiments show similar or better performance than existing methods, while being orders of magnitude faster.

Sequential Learning of Active Subspaces

In recent years, active subspace methods (ASMs) have become a popular means of performing subspace sensitivity analysis on black-box functions. Naively applied, however, ASMs require gradient evaluations of the target function. In the event of noisy, expensive, or stochastic simulators, evaluating gradients via finite differencing may be infeasible. In such cases, often a surrogate model is employed, on which finite differencing is performed. When the surrogate model is a Gaussian process, we show that the ASM estimator is available in closed form, rendering the finite-difference approximation unnecessary. We use our closed-form solution to develop acquisition functions focused on sequential learning tailored to sensitivity analysis on top of ASMs. We also show that the traditional ASM estimator may be viewed as a method of moments estimator for a certain class of Gaussian processes. We demonstrate how uncertainty on Gaussian process hyperparameters may be propagated to uncertainty on the sensitivity analysis, allowing model-based confidence intervals on the active subspace. Our methodological developments are illustrated on several examples.

Evaluating Gaussian Process Metamodels and Sequential Designs for Noisy Level Set Estimation

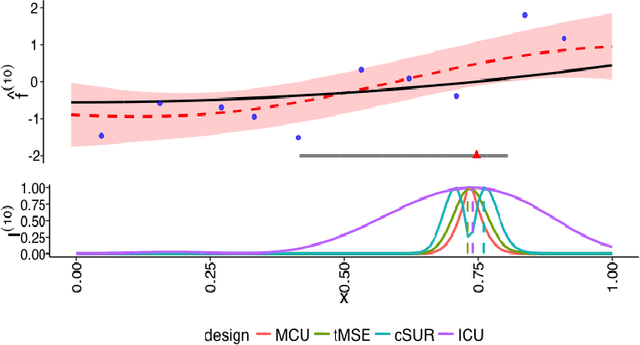
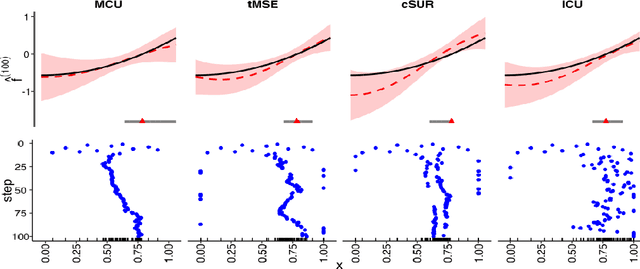
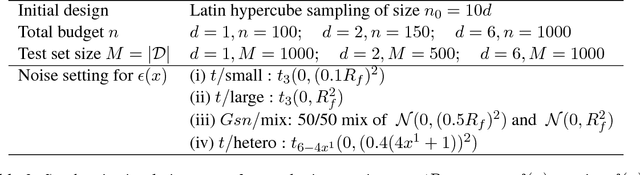
We consider the problem of learning the level set for which a noisy black-box function exceeds a given threshold. To efficiently reconstruct the level set, we investigate Gaussian process (GP) metamodels. Our focus is on strongly stochastic samplers, in particular with heavy-tailed simulation noise and low signal-to-noise ratio. To guard against noise misspecification, we assess the performance of three variants: (i) GPs with Student-$t$ observations; (ii) Student-$t$ processes (TPs); and (iii) classification GPs modeling the sign of the response. As a fourth extension, we study GP surrogates with monotonicity constraints that are relevant when the level set is known to be connected. In conjunction with these metamodels, we analyze several acquisition functions for guiding the sequential experimental designs, extending existing stepwise uncertainty reduction criteria to the stochastic contour-finding context. This also motivates our development of (approximate) updating formulas to efficiently compute such acquisition functions. Our schemes are benchmarked by using a variety of synthetic experiments in 1--6 dimensions. We also consider an application of level set estimation for determining the optimal exercise policy and valuation of Bermudan options in finance.

A Bayesian optimization approach to find Nash equilibria

Game theory finds nowadays a broad range of applications in engineering and machine learning. However, in a derivative-free, expensive black-box context, very few algorithmic solutions are available to find game equilibria. Here, we propose a novel Gaussian-process based approach for solving games in this context. We follow a classical Bayesian optimization framework, with sequential sampling decisions based on acquisition functions. Two strategies are proposed, based either on the probability of achieving equilibrium or on the Stepwise Uncertainty Reduction paradigm. Practical and numerical aspects are discussed in order to enhance the scalability and reduce computation time. Our approach is evaluated on several synthetic game problems with varying number of players and decision space dimensions. We show that equilibria can be found reliably for a fraction of the cost (in terms of black-box evaluations) compared to classical, derivative-based algorithms. The method is available in the R package GPGame available on CRAN at https://cran.r-project.org/package=GPGame.