Trajectory-oriented optimization of stochastic epidemiological models

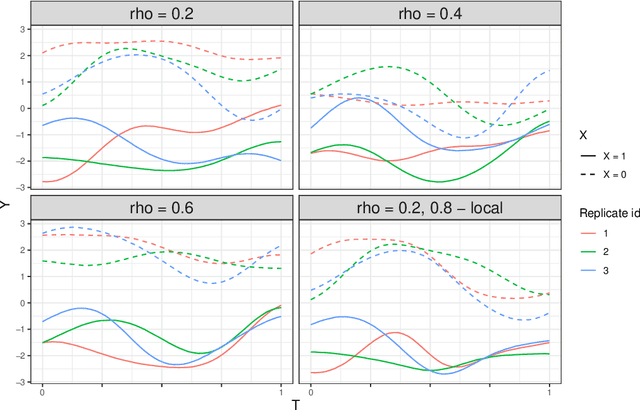
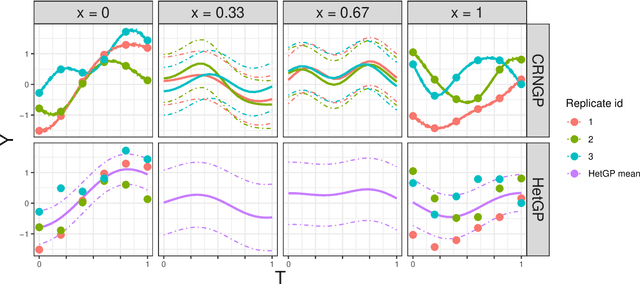
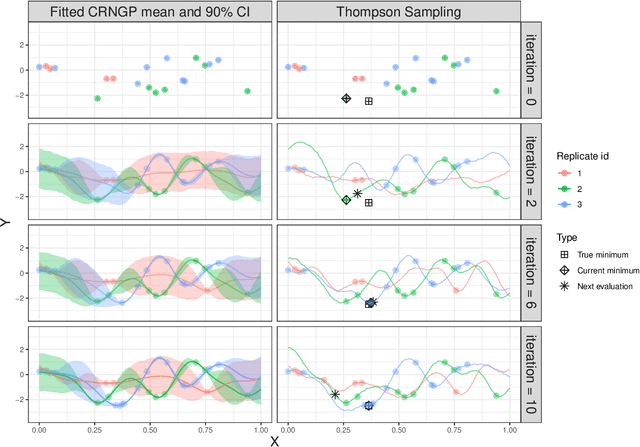
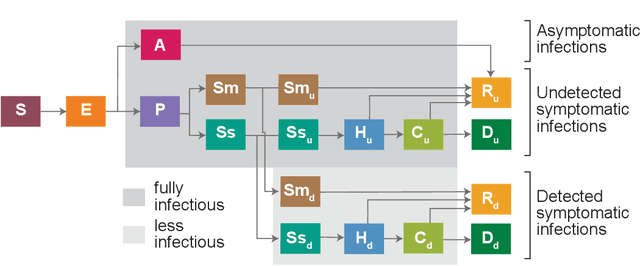
Epidemiological models must be calibrated to ground truth for downstream tasks such as producing forward projections or running what-if scenarios. The meaning of calibration changes in case of a stochastic model since output from such a model is generally described via an ensemble or a distribution. Each member of the ensemble is usually mapped to a random number seed (explicitly or implicitly). With the goal of finding not only the input parameter settings but also the random seeds that are consistent with the ground truth, we propose a class of Gaussian process (GP) surrogates along with an optimization strategy based on Thompson sampling. This Trajectory Oriented Optimization (TOO) approach produces actual trajectories close to the empirical observations instead of a set of parameter settings where only the mean simulation behavior matches with the ground truth.

Lazy Estimation of Variable Importance for Large Neural Networks

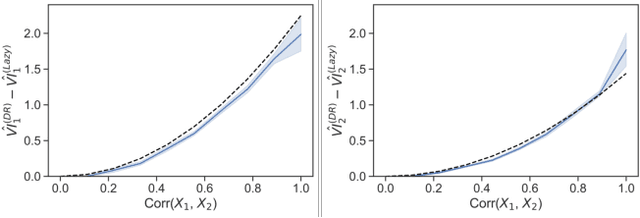
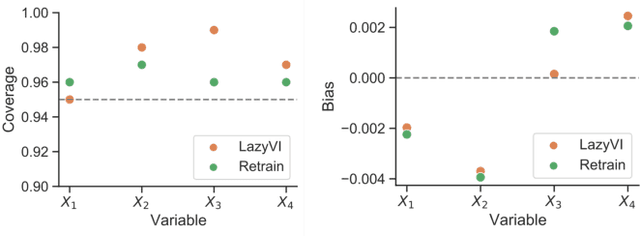
As opaque predictive models increasingly impact many areas of modern life, interest in quantifying the importance of a given input variable for making a specific prediction has grown. Recently, there has been a proliferation of model-agnostic methods to measure variable importance (VI) that analyze the difference in predictive power between a full model trained on all variables and a reduced model that excludes the variable(s) of interest. A bottleneck common to these methods is the estimation of the reduced model for each variable (or subset of variables), which is an expensive process that often does not come with theoretical guarantees. In this work, we propose a fast and flexible method for approximating the reduced model with important inferential guarantees. We replace the need for fully retraining a wide neural network by a linearization initialized at the full model parameters. By adding a ridge-like penalty to make the problem convex, we prove that when the ridge penalty parameter is sufficiently large, our method estimates the variable importance measure with an error rate of $O(\frac{1}{\sqrt{n}})$ where $n$ is the number of training samples. We also show that our estimator is asymptotically normal, enabling us to provide confidence bounds for the VI estimates. We demonstrate through simulations that our method is fast and accurate under several data-generating regimes, and we demonstrate its real-world applicability on a seasonal climate forecasting example.

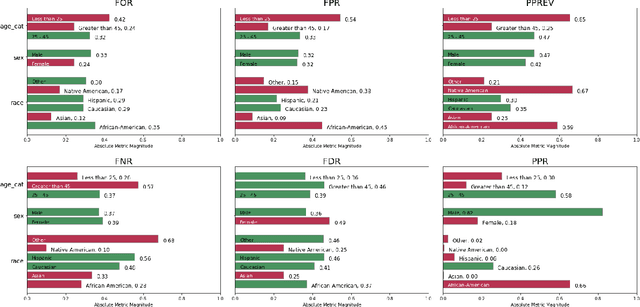
Aequitas: A Bias and Fairness Audit Toolkit

Recent work has raised concerns on the risk of unintended bias in algorithmic decision making systems being used nowadays that can affect individuals unfairly based on race, gender or religion, among other possible characteristics. While a lot of bias metrics and fairness definitions have been proposed in recent years, there is no consensus on which metric/definition should be used and there are very few available resources to operationalize them. Therefore, despite recent awareness, auditing for bias and fairness when developing and deploying algorithmic decision making systems is not yet a standard practice. We present Aequitas, an open source bias and fairness audit toolkit that is an intuitive and easy to use addition to the machine learning workflow, enabling users to seamlessly test models for several bias and fairness metrics in relation to multiple population sub-groups. We believe Aequitas will facilitate informed and equitable decisions around developing and deploying algorithmic decision making systems for both data scientists, machine learning researchers and policymakers.