Lazy Estimation of Variable Importance for Large Neural Networks
Paper and Code
Jul 19, 2022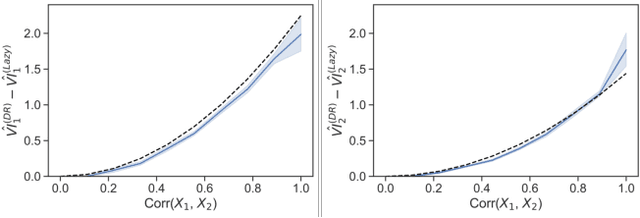
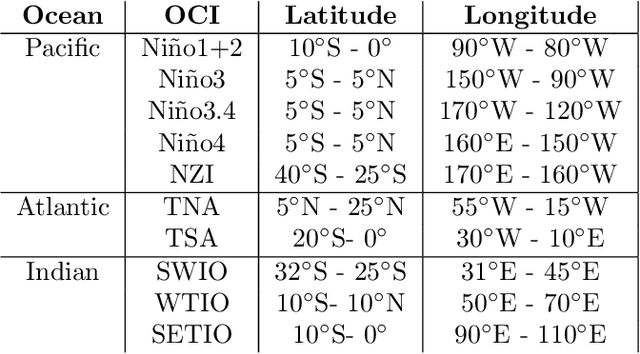
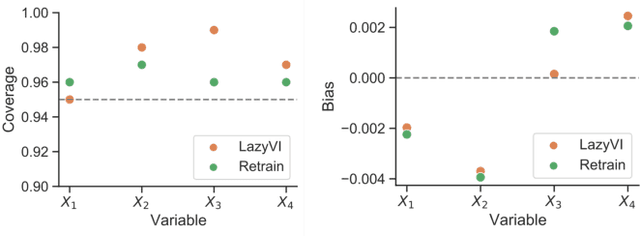

As opaque predictive models increasingly impact many areas of modern life, interest in quantifying the importance of a given input variable for making a specific prediction has grown. Recently, there has been a proliferation of model-agnostic methods to measure variable importance (VI) that analyze the difference in predictive power between a full model trained on all variables and a reduced model that excludes the variable(s) of interest. A bottleneck common to these methods is the estimation of the reduced model for each variable (or subset of variables), which is an expensive process that often does not come with theoretical guarantees. In this work, we propose a fast and flexible method for approximating the reduced model with important inferential guarantees. We replace the need for fully retraining a wide neural network by a linearization initialized at the full model parameters. By adding a ridge-like penalty to make the problem convex, we prove that when the ridge penalty parameter is sufficiently large, our method estimates the variable importance measure with an error rate of $O(\frac{1}{\sqrt{n}})$ where $n$ is the number of training samples. We also show that our estimator is asymptotically normal, enabling us to provide confidence bounds for the VI estimates. We demonstrate through simulations that our method is fast and accurate under several data-generating regimes, and we demonstrate its real-world applicability on a seasonal climate forecasting example.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge