Fast, Distribution-free Predictive Inference for Neural Networks with Coverage Guarantees

This paper introduces a novel, computationally-efficient algorithm for predictive inference (PI) that requires no distributional assumptions on the data and can be computed faster than existing bootstrap-type methods for neural networks. Specifically, if there are $n$ training samples, bootstrap methods require training a model on each of the $n$ subsamples of size $n-1$; for large models like neural networks, this process can be computationally prohibitive. In contrast, our proposed method trains one neural network on the full dataset with $(\epsilon, \delta)$-differential privacy (DP) and then approximates each leave-one-out model efficiently using a linear approximation around the differentially-private neural network estimate. With exchangeable data, we prove that our approach has a rigorous coverage guarantee that depends on the preset privacy parameters and the stability of the neural network, regardless of the data distribution. Simulations and experiments on real data demonstrate that our method satisfies the coverage guarantees with substantially reduced computation compared to bootstrap methods.

Lazy Estimation of Variable Importance for Large Neural Networks

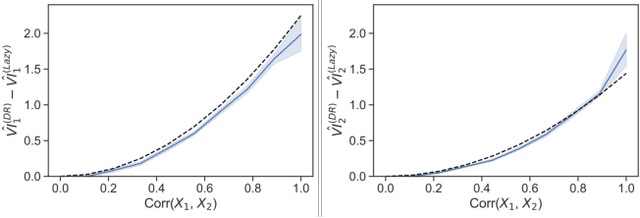
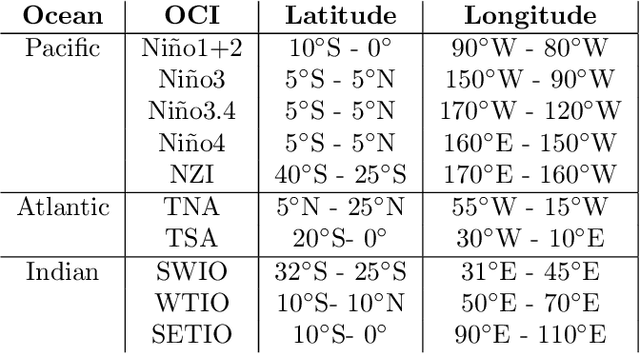
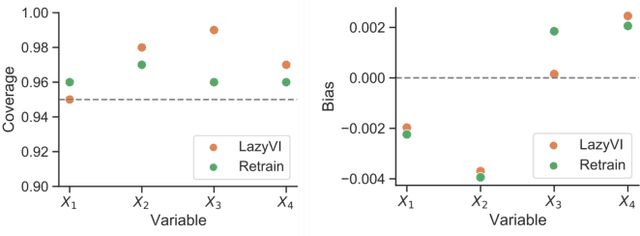
As opaque predictive models increasingly impact many areas of modern life, interest in quantifying the importance of a given input variable for making a specific prediction has grown. Recently, there has been a proliferation of model-agnostic methods to measure variable importance (VI) that analyze the difference in predictive power between a full model trained on all variables and a reduced model that excludes the variable(s) of interest. A bottleneck common to these methods is the estimation of the reduced model for each variable (or subset of variables), which is an expensive process that often does not come with theoretical guarantees. In this work, we propose a fast and flexible method for approximating the reduced model with important inferential guarantees. We replace the need for fully retraining a wide neural network by a linearization initialized at the full model parameters. By adding a ridge-like penalty to make the problem convex, we prove that when the ridge penalty parameter is sufficiently large, our method estimates the variable importance measure with an error rate of $O(\frac{1}{\sqrt{n}})$ where $n$ is the number of training samples. We also show that our estimator is asymptotically normal, enabling us to provide confidence bounds for the VI estimates. We demonstrate through simulations that our method is fast and accurate under several data-generating regimes, and we demonstrate its real-world applicability on a seasonal climate forecasting example.

Gaussian Process Inference Using Mini-batch Stochastic Gradient Descent: Convergence Guarantees and Empirical Benefits

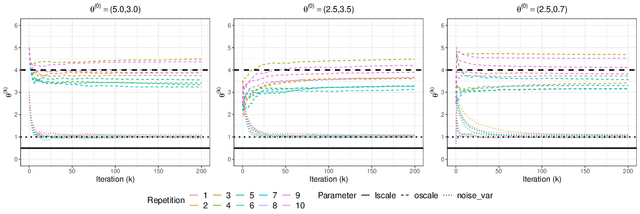
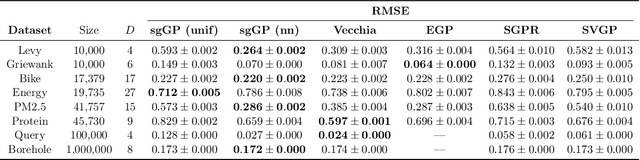
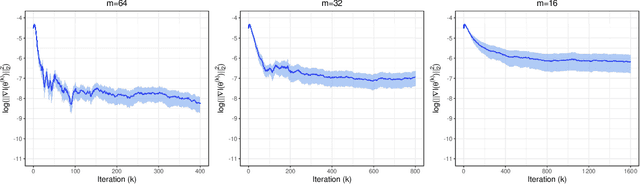
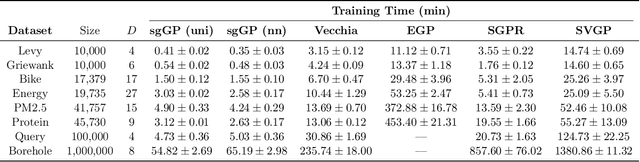
Stochastic gradient descent (SGD) and its variants have established themselves as the go-to algorithms for large-scale machine learning problems with independent samples due to their generalization performance and intrinsic computational advantage. However, the fact that the stochastic gradient is a biased estimator of the full gradient with correlated samples has led to the lack of theoretical understanding of how SGD behaves under correlated settings and hindered its use in such cases. In this paper, we focus on hyperparameter estimation for the Gaussian process (GP) and take a step forward towards breaking the barrier by proving minibatch SGD converges to a critical point of the full log-likelihood loss function, and recovers model hyperparameters with rate $O(\frac{1}{K})$ for $K$ iterations, up to a statistical error term depending on the minibatch size. Our theoretical guarantees hold provided that the kernel functions exhibit exponential or polynomial eigendecay which is satisfied by a wide range of kernels commonly used in GPs. Numerical studies on both simulated and real datasets demonstrate that minibatch SGD has better generalization over state-of-the-art GP methods while reducing the computational burden and opening a new, previously unexplored, data size regime for GPs.

The Internet of Federated Things : A Vision for the Future and In-depth Survey of Data-driven Approaches for Federated Learning

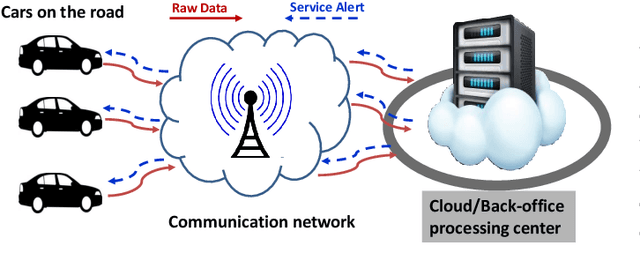
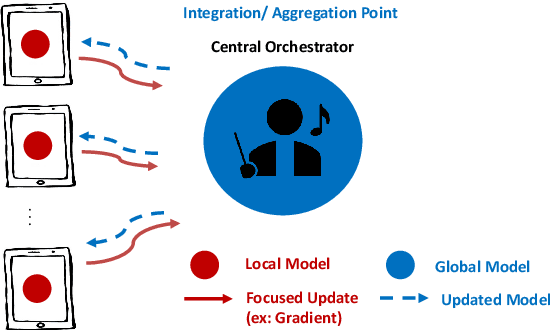
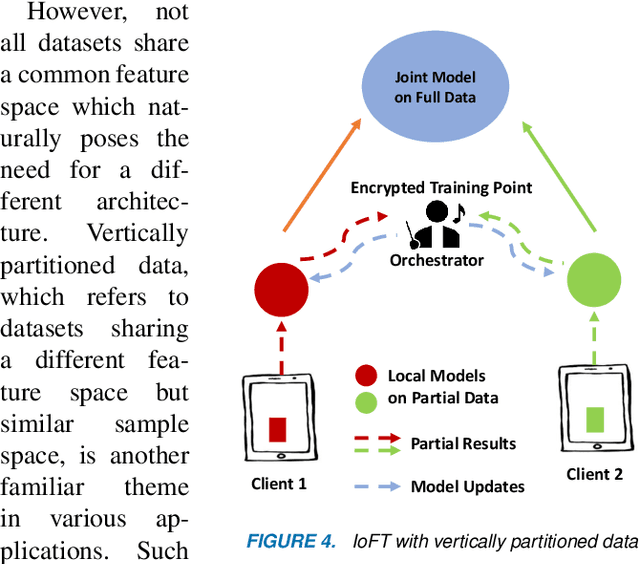
The Internet of Things (IoT) is on the verge of a major paradigm shift. In the IoT system of the future, IoFT, the cloud will be substituted by the crowd where model training is brought to the edge, allowing IoT devices to collaboratively extract knowledge and build smart analytics/models while keeping their personal data stored locally. This paradigm shift was set into motion by the tremendous increase in computational power on IoT devices and the recent advances in decentralized and privacy-preserving model training, coined as federated learning (FL). This article provides a vision for IoFT and a systematic overview of current efforts towards realizing this vision. Specifically, we first introduce the defining characteristics of IoFT and discuss FL data-driven approaches, opportunities, and challenges that allow decentralized inference within three dimensions: (i) a global model that maximizes utility across all IoT devices, (ii) a personalized model that borrows strengths across all devices yet retains its own model, (iii) a meta-learning model that quickly adapts to new devices or learning tasks. We end by describing the vision and challenges of IoFT in reshaping different industries through the lens of domain experts. Those industries include manufacturing, transportation, energy, healthcare, quality & reliability, business, and computing.

Improved Prediction and Network Estimation Using the Monotone Single Index Multi-variate Autoregressive Model

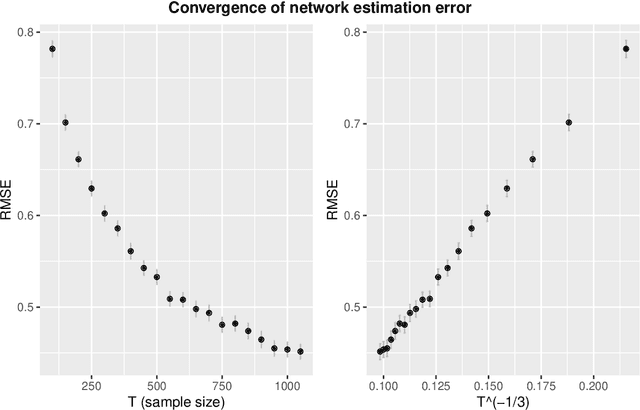
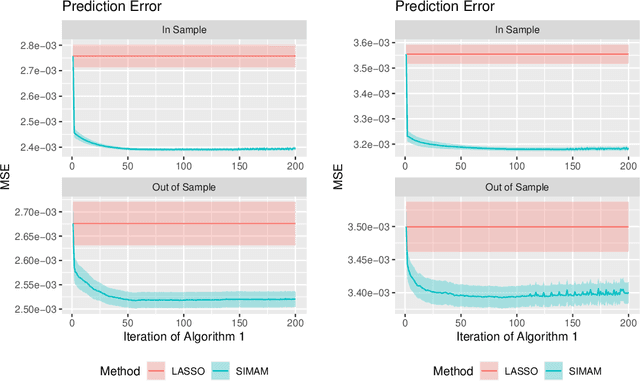
Network estimation from multi-variate point process or time series data is a problem of fundamental importance. Prior work has focused on parametric approaches that require a known parametric model, which makes estimation procedures less robust to model mis-specification, non-linearities and heterogeneities. In this paper, we develop a semi-parametric approach based on the monotone single-index multi-variate autoregressive model (SIMAM) which addresses these challenges. We provide theoretical guarantees for dependent data and an alternating projected gradient descent algorithm. Significantly we do not explicitly assume mixing conditions on the process (although we do require conditions analogous to restricted strong convexity) and we achieve rates of the form $O(T^{-\frac{1}{3}} \sqrt{s\log(TM)})$ (optimal in the independent design case) where $s$ is the threshold for the maximum in-degree of the network that indicates the sparsity level, $M$ is the number of actors and $T$ is the number of time points. In addition, we demonstrate the superior performance both on simulated data and two real data examples where our SIMAM approach out-performs state-of-the-art parametric methods both in terms of prediction and network estimation.

Prediction in the presence of response-dependent missing labels

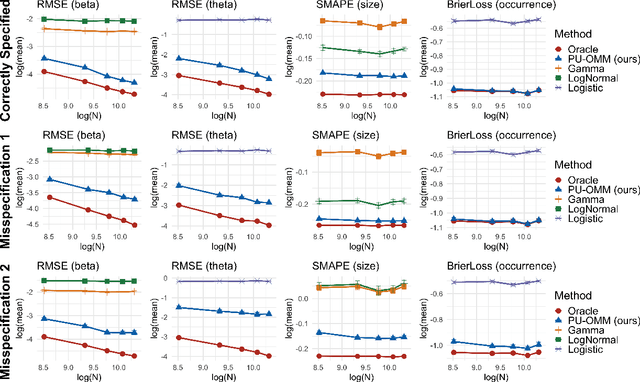
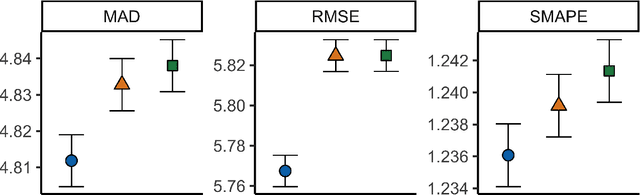
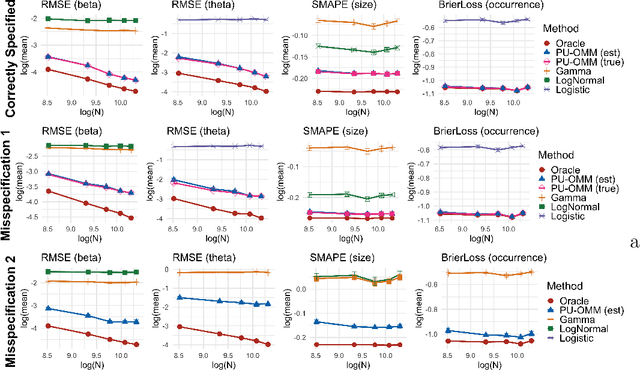
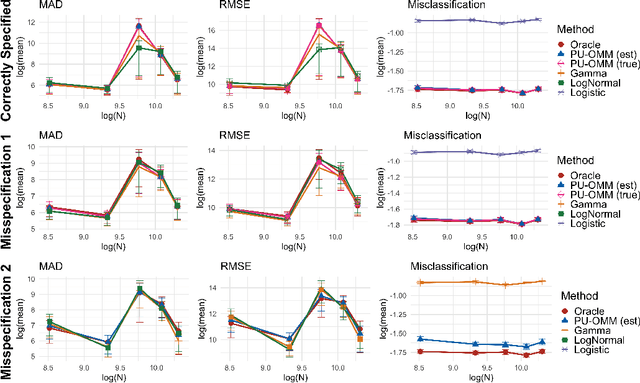
In a variety of settings, limitations of sensing technologies or other sampling mechanisms result in missing labels, where the likelihood of a missing label in the training set is an unknown function of the data. For example, satellites used to detect forest fires cannot sense fires below a certain size threshold. In such cases, training datasets consist of positive and pseudo-negative observations where pseudo-negative observations can be either true negatives or undetected positives with small magnitudes. We develop a new methodology and non-convex algorithm P(ositive) U(nlabeled) - O(ccurrence) M(agnitude) M(ixture) which jointly estimates the occurrence and detection likelihood of positive samples, utilizing prior knowledge of the detection mechanism. Our approach uses ideas from positive-unlabeled (PU)-learning and zero-inflated models that jointly estimate the magnitude and occurrence of events. We provide conditions under which our model is identifiable and prove that even though our approach leads to a non-convex objective, any local minimizer has optimal statistical error (up to a log term) and projected gradient descent has geometric convergence rates. We demonstrate on both synthetic data and a California wildfire dataset that our method out-performs existing state-of-the-art approaches.

A Sharp Blockwise Tensor Perturbation Bound for Orthogonal Iteration

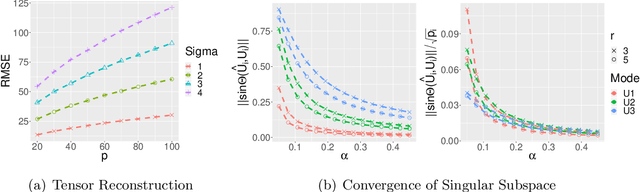
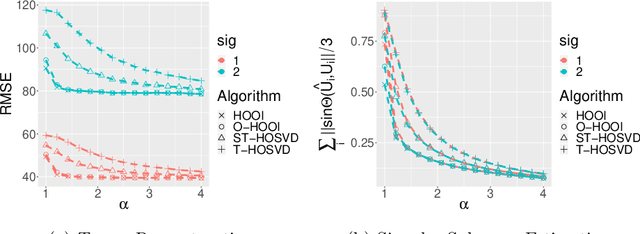
In this paper, we develop novel perturbation bounds for the high-order orthogonal iteration (HOOI) [DLDMV00b]. Under mild regularity conditions, we establish blockwise tensor perturbation bounds for HOOI with guarantees for both tensor reconstruction in Hilbert-Schmidt norm $\|\widehat{\bcT} - \bcT \|_{\tHS}$ and mode-$k$ singular subspace estimation in Schatten-$q$ norm $\| \sin \Theta (\widehat{\U}_k, \U_k) \|_q$ for any $q \geq 1$. We show the upper bounds of mode-$k$ singular subspace estimation are unilateral and converge linearly to a quantity characterized by blockwise errors of the perturbation and signal strength. For the tensor reconstruction error bound, we express the bound through a simple quantity $\xi$, which depends only on perturbation and the multilinear rank of the underlying signal. Rate matching deterministic lower bound for tensor reconstruction, which demonstrates the optimality of HOOI, is also provided. Furthermore, we prove that one-step HOOI (i.e., HOOI with only a single iteration) is also optimal in terms of tensor reconstruction and can be used to lower the computational cost. The perturbation results are also extended to the case that only partial modes of $\bcT$ have low-rank structure. We support our theoretical results by extensive numerical studies. Finally, we apply the novel perturbation bounds of HOOI on two applications, tensor denoising and tensor co-clustering, from machine learning and statistics, which demonstrates the superiority of the new perturbation results.

Context-dependent self-exciting point processes: models, methods, and risk bounds in high dimensions

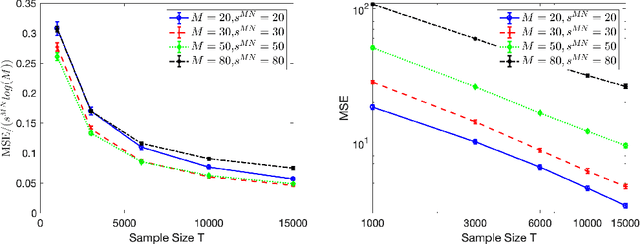
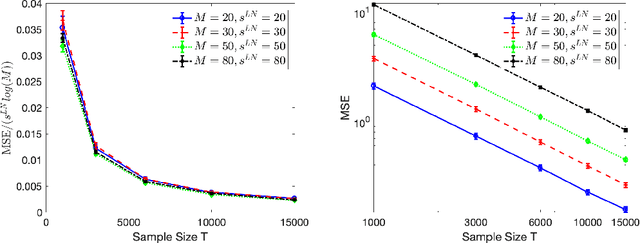
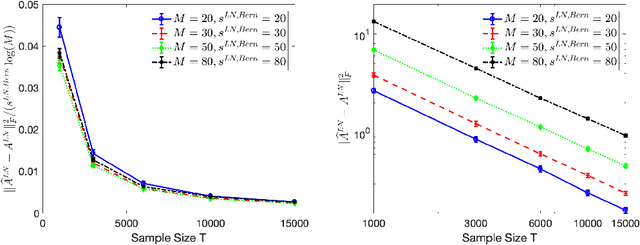
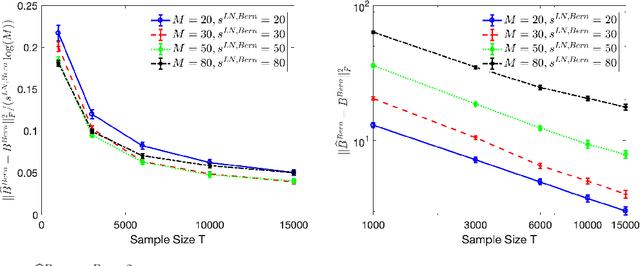
High-dimensional autoregressive point processes model how current events trigger or inhibit future events, such as activity by one member of a social network can affect the future activity of his or her neighbors. While past work has focused on estimating the underlying network structure based solely on the times at which events occur on each node of the network, this paper examines the more nuanced problem of estimating context-dependent networks that reflect how features associated with an event (such as the content of a social media post) modulate the strength of influences among nodes. Specifically, we leverage ideas from compositional time series and regularization methods in machine learning to conduct network estimation for high-dimensional marked point processes. Two models and corresponding estimators are considered in detail: an autoregressive multinomial model suited to categorical marks and a logistic-normal model suited to marks with mixed membership in different categories. Importantly, the logistic-normal model leads to a convex negative log-likelihood objective and captures dependence across categories. We provide theoretical guarantees for both estimators, which we validate by simulations and a synthetic data-generating model. We further validate our methods through two real data examples and demonstrate the advantages and disadvantages of both approaches.

ISLET: Fast and Optimal Low-rank Tensor Regression via Importance Sketching

In this paper, we develop a novel procedure for low-rank tensor regression, namely \underline{I}mportance \underline{S}ketching \underline{L}ow-rank \underline{E}stimation for \underline{T}ensors (ISLET). The central idea behind ISLET is \emph{importance sketching}, i.e., carefully designed sketches based on both the responses and low-dimensional structure of the parameter of interest. We show that the proposed method is sharply minimax optimal in terms of the mean-squared error under low-rank Tucker assumptions and under randomized Gaussian ensemble design. In addition, if a tensor is low-rank with group sparsity, our procedure also achieves minimax optimality. Further, we show through numerical studies that ISLET achieves comparable or better mean-squared error performance to existing state-of-the-art methods whilst having substantial storage and run-time advantages including capabilities for parallel and distributed computing. In particular, our procedure performs reliable estimation with tensors of dimension $p = O(10^8)$ and is $1$ or $2$ orders of magnitude faster than baseline methods.

Minimizing Negative Transfer of Knowledge in Multivariate Gaussian Processes: A Scalable and Regularized Approach

Recently there has been an increasing interest in the multivariate Gaussian process (MGP) which extends the Gaussian process (GP) to deal with multiple outputs. One approach to construct the MGP and account for non-trivial commonalities amongst outputs employs a convolution process (CP). The CP is based on the idea of sharing latent functions across several convolutions. Despite the elegance of the CP construction, it provides new challenges that need yet to be tackled. First, even with a moderate number of outputs, model building is extremely prohibitive due to the huge increase in computational demands and number of parameters to be estimated. Second, the negative transfer of knowledge may occur when some outputs do not share commonalities. In this paper we address these issues. We propose a regularized pairwise modeling approach for the MGP established using CP. The key feature of our approach is to distribute the estimation of the full multivariate model into a group of bivariate GPs which are individually built. Interestingly pairwise modeling turns out to possess unique characteristics, which allows us to tackle the challenge of negative transfer through penalizing the latent function that facilitates information sharing in each bivariate model. Predictions are then made through combining predictions from the bivariate models within a Bayesian framework. The proposed method has excellent scalability when the number of outputs is large and minimizes the negative transfer of knowledge between uncorrelated outputs. Statistical guarantees for the proposed method are studied and its advantageous features are demonstrated through numerical studies.