Is Algorithmic Stability Testable? A Unified Framework under Computational Constraints

Algorithmic stability is a central notion in learning theory that quantifies the sensitivity of an algorithm to small changes in the training data. If a learning algorithm satisfies certain stability properties, this leads to many important downstream implications, such as generalization, robustness, and reliable predictive inference. Verifying that stability holds for a particular algorithm is therefore an important and practical question. However, recent results establish that testing the stability of a black-box algorithm is impossible, given limited data from an unknown distribution, in settings where the data lies in an uncountably infinite space (such as real-valued data). In this work, we extend this question to examine a far broader range of settings, where the data may lie in any space -- for example, categorical data. We develop a unified framework for quantifying the hardness of testing algorithmic stability, which establishes that across all settings, if the available data is limited then exhaustive search is essentially the only universally valid mechanism for certifying algorithmic stability. Since in practice, any test of stability would naturally be subject to computational constraints, exhaustive search is impossible and so this implies fundamental limits on our ability to test the stability property for a black-box algorithm.

The Limits of Assumption-free Tests for Algorithm Performance

Algorithm evaluation and comparison are fundamental questions in machine learning and statistics -- how well does an algorithm perform at a given modeling task, and which algorithm performs best? Many methods have been developed to assess algorithm performance, often based around cross-validation type strategies, retraining the algorithm of interest on different subsets of the data and assessing its performance on the held-out data points. Despite the broad use of such procedures, the theoretical properties of these methods are not yet fully understood. In this work, we explore some fundamental limits for answering these questions with limited amounts of data. In particular, we make a distinction between two questions: how good is an algorithm $A$ at the problem of learning from a training set of size $n$, versus, how good is a particular fitted model produced by running $A$ on a particular training data set of size $n$? Our main results prove that, for any test that treats the algorithm $A$ as a ``black box'' (i.e., we can only study the behavior of $A$ empirically), there is a fundamental limit on our ability to carry out inference on the performance of $A$, unless the number of available data points $N$ is many times larger than the sample size $n$ of interest. (On the other hand, evaluating the performance of a particular fitted model is easy as long as a holdout data set is available -- that is, as long as $N-n$ is not too small.) We also ask whether an assumption of algorithmic stability might be sufficient to circumvent this hardness result. Surprisingly, we find that this is not the case: the same hardness result still holds for the problem of evaluating the performance of $A$, aside from a high-stability regime where fitted models are essentially nonrandom. Finally, we also establish similar hardness results for the problem of comparing multiple algorithms.

Computational Lower Bounds for Graphon Estimation via Low-degree Polynomials

Graphon estimation has been one of the most fundamental problems in network analysis and has received considerable attention in the past decade. From the statistical perspective, the minimax error rate of graphon estimation has been established by Gao et al (2015) for both stochastic block model (SBM) and nonparametric graphon estimation. The statistical optimal estimators are based on constrained least squares and have computational complexity exponential in the dimension. From the computational perspective, the best-known polynomial-time estimator is based on universal singular value thresholding (USVT), but it can only achieve a much slower estimation error rate than the minimax one. It is natural to wonder if such a gap is essential. The computational optimality of the USVT or the existence of a computational barrier in graphon estimation has been a long-standing open problem. In this work, we take the first step towards it and provide rigorous evidence for the computational barrier in graphon estimation via low-degree polynomials. Specifically, in both SBM and nonparametric graphon estimation, we show that for low-degree polynomial estimators, their estimation error rates cannot be significantly better than that of the USVT under a wide range of parameter regimes. Our results are proved based on the recent development of low-degree polynomials by Schramm and Wein (2022), while we overcome a few key challenges in applying it to the general graphon estimation problem. By leveraging our main results, we also provide a computational lower bound on the clustering error for community detection in SBM with a growing number of communities and this yields a new piece of evidence for the conjectured Kesten-Stigum threshold for efficient community recovery.

Iterative Approximate Cross-Validation

Cross-validation (CV) is one of the most popular tools for assessing and selecting predictive models. However, standard CV suffers from high computational cost when the number of folds is large. Recently, under the empirical risk minimization (ERM) framework, a line of works proposed efficient methods to approximate CV based on the solution of the ERM problem trained on the full dataset. However, in large-scale problems, it can be hard to obtain the exact solution of the ERM problem, either due to limited computational resources or due to early stopping as a way of preventing overfitting. In this paper, we propose a new paradigm to efficiently approximate CV when the ERM problem is solved via an iterative first-order algorithm, without running until convergence. Our new method extends existing guarantees for CV approximation to hold along the whole trajectory of the algorithm, including at convergence, thus generalizing existing CV approximation methods. Finally, we illustrate the accuracy and computational efficiency of our method through a range of empirical studies.

Nonconvex Matrix Factorization is Geodesically Convex: Global Landscape Analysis for Fixed-rank Matrix Optimization From a Riemannian Perspective

We study a general matrix optimization problem with a fixed-rank positive semidefinite (PSD) constraint. We perform the Burer-Monteiro factorization and consider a particular Riemannian quotient geometry in a search space that has a total space equipped with the Euclidean metric. When the original objective f satisfies standard restricted strong convexity and smoothness properties, we characterize the global landscape of the factorized objective under the Riemannian quotient geometry. We show the entire search space can be divided into three regions: (R1) the region near the target parameter of interest, where the factorized objective is geodesically strongly convex and smooth; (R2) the region containing neighborhoods of all strict saddle points; (R3) the remaining regions, where the factorized objective has a large gradient. To our best knowledge, this is the first global landscape analysis of the Burer-Monteiro factorized objective under the Riemannian quotient geometry. Our results provide a fully geometric explanation for the superior performance of vanilla gradient descent under the Burer-Monteiro factorization. When f satisfies a weaker restricted strict convexity property, we show there exists a neighborhood near local minimizers such that the factorized objective is geodesically convex. To prove our results we provide a comprehensive landscape analysis of a matrix factorization problem with a least squares objective, which serves as a critical bridge. Our conclusions are also based on a result of independent interest stating that the geodesic ball centered at Y with a radius 1/3 of the least singular value of Y is a geodesically convex set under the Riemannian quotient geometry, which as a corollary, also implies a quantitative bound of the convexity radius in the Bures-Wasserstein space. The convexity radius obtained is sharp up to constants.

Tensor-on-Tensor Regression: Riemannian Optimization, Over-parameterization, Statistical-computational Gap, and Their Interplay

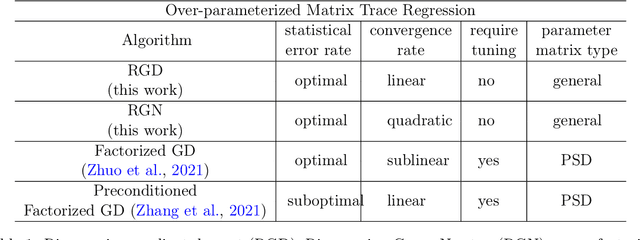
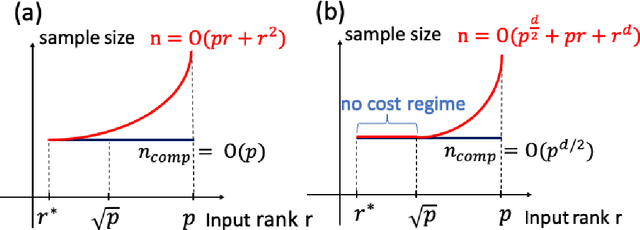
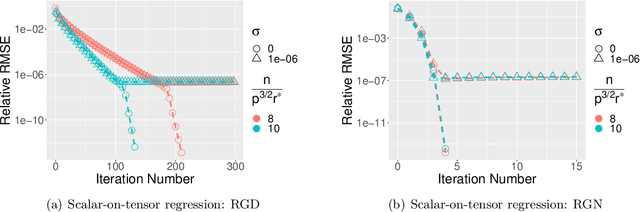
We study the tensor-on-tensor regression, where the goal is to connect tensor responses to tensor covariates with a low Tucker rank parameter tensor/matrix without the prior knowledge of its intrinsic rank. We propose the Riemannian gradient descent (RGD) and Riemannian Gauss-Newton (RGN) methods and cope with the challenge of unknown rank by studying the effect of rank over-parameterization. We provide the first convergence guarantee for the general tensor-on-tensor regression by showing that RGD and RGN respectively converge linearly and quadratically to a statistically optimal estimate in both rank correctly-parameterized and over-parameterized settings. Our theory reveals an intriguing phenomenon: Riemannian optimization methods naturally adapt to over-parameterization without modifications to their implementation. We also give the first rigorous evidence for the statistical-computational gap in scalar-on-tensor regression under the low-degree polynomials framework. Our theory demonstrates a ``blessing of statistical-computational gap" phenomenon: in a wide range of scenarios in tensor-on-tensor regression for tensors of order three or higher, the computationally required sample size matches what is needed by moderate rank over-parameterization when considering computationally feasible estimators, while there are no such benefits in the matrix settings. This shows moderate rank over-parameterization is essentially ``cost-free" in terms of sample size in tensor-on-tensor regression of order three or higher. Finally, we conduct simulation studies to show the advantages of our proposed methods and to corroborate our theoretical findings.

On Geometric Connections of Embedded and Quotient Geometries in Riemannian Fixed-rank Matrix Optimization

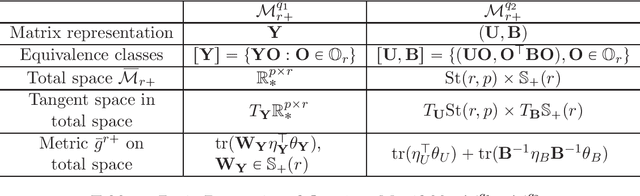
In this paper, we propose a general procedure for establishing the landscape connections of a Riemannian optimization problem under the embedded and quotient geometries. By applying the general procedure to the fixed-rank positive semidefinite (PSD) and general matrix optimization, we establish an exact Riemannian gradient connection under two geometries at every point on the manifold and sandwich inequalities between the spectra of Riemannian Hessians at Riemannian first-order stationary points (FOSPs). These results immediately imply an equivalence on the sets of Riemannian FOSPs, Riemannian second-order stationary points (SOSPs) and strict saddles of fixed-rank matrix optimization under the embedded and the quotient geometries. To the best of our knowledge, this is the first geometric landscape connection between the embedded and the quotient geometries for fixed-rank matrix optimization and it provides a concrete example on how these two geometries are connected in Riemannian optimization. In addition, the effects of the Riemannian metric and quotient structure on the landscape connection are discussed. We also observe an algorithmic connection for fixed-rank matrix optimization under two geometries with some specific Riemannian metrics. A number of novel ideas and technical ingredients including a unified treatment for different Riemannian metrics and new horizontal space representations under quotient geometries are developed to obtain our results. The results in this paper deepen our understanding of geometric connections of Riemannian optimization under different Riemannian geometries and provide a few new theoretical insights to unanswered questions in the literature.

Nonconvex Factorization and Manifold Formulations are Almost Equivalent in Low-rank Matrix Optimization

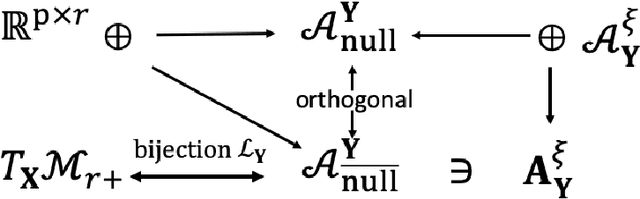
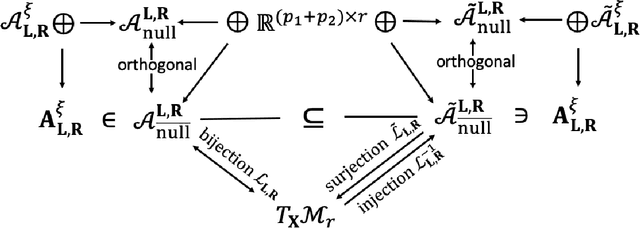
In this paper, we consider the geometric landscape connection of the widely studied manifold and factorization formulations in low-rank positive semidefinite (PSD) and general matrix optimization. We establish an equivalence on the set of first-order stationary points (FOSPs) and second-order stationary points (SOSPs) between the manifold and the factorization formulations. We further give a sandwich inequality on the spectrum of Riemannian and Euclidean Hessians at FOSPs, which can be used to transfer more geometric properties from one formulation to another. Similarities and differences on the landscape connection under the PSD case and the general case are discussed. To the best of our knowledge, this is the first geometric landscape connection between the manifold and the factorization formulations for handling rank constraints. In the general low-rank matrix optimization, the landscape connection of two factorization formulations (unregularized and regularized ones) is also provided. By applying these geometric landscape connections, we are able to solve unanswered questions in literature and establish stronger results in the applications on geometric analysis of phase retrieval, well-conditioned low-rank matrix optimization, and the role of regularization in factorization arising from machine learning and signal processing.

Low-rank Tensor Estimation via Riemannian Gauss-Newton: Statistical Optimality and Second-Order Convergence

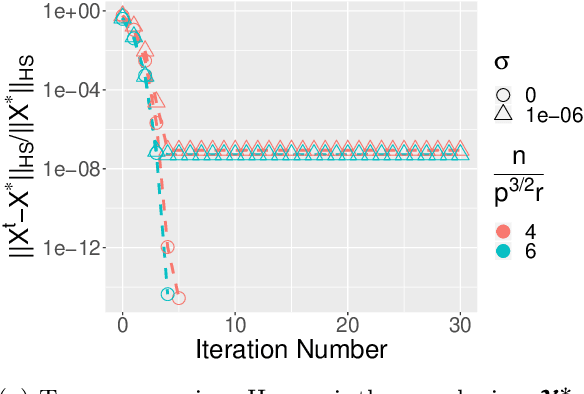
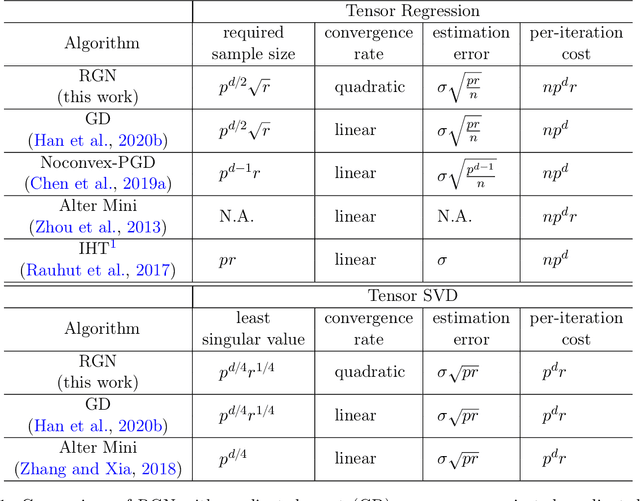
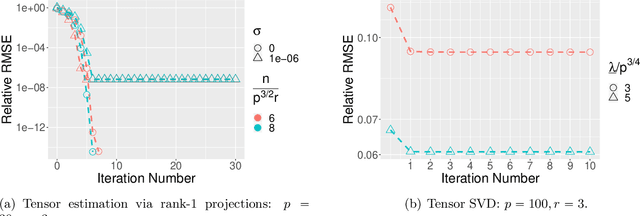
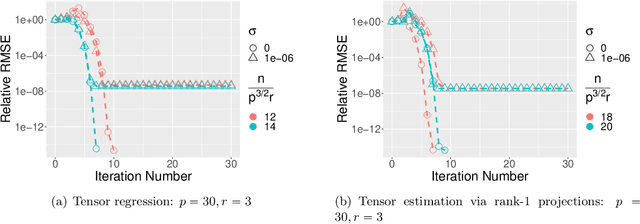
In this paper, we consider the estimation of a low Tucker rank tensor from a number of noisy linear measurements. The general problem covers many specific examples arising from applications, including tensor regression, tensor completion, and tensor PCA/SVD. We propose a Riemannian Gauss-Newton (RGN) method with fast implementations for low Tucker rank tensor estimation. Different from the generic (super)linear convergence guarantee of RGN in the literature, we prove the first quadratic convergence guarantee of RGN for low-rank tensor estimation under some mild conditions. A deterministic estimation error lower bound, which matches the upper bound, is provided that demonstrates the statistical optimality of RGN. The merit of RGN is illustrated through two machine learning applications: tensor regression and tensor SVD. Finally, we provide the simulation results to corroborate our theoretical findings.

Exact Clustering in Tensor Block Model: Statistical Optimality and Computational Limit

High-order clustering aims to identify heterogeneous substructure in multiway dataset that arises commonly in neuroimaging, genomics, and social network studies. The non-convex and discontinuous nature of the problem poses significant challenges in both statistics and computation. In this paper, we propose a tensor block model and the computationally efficient methods, \emph{high-order Lloyd algorithm} (HLloyd) and \emph{high-order spectral clustering} (HSC), for high-order clustering in tensor block model. The convergence of the proposed procedure is established, and we show that our method achieves exact clustering under reasonable assumptions. We also give the complete characterization for the statistical-computational trade-off in high-order clustering based on three different signal-to-noise ratio regimes. Finally, we show the merits of the proposed procedures via extensive experiments on both synthetic and real datasets.