Nicolas Garcia Trillos
An Optimal Transport Approach for Computing Adversarial Training Lower Bounds in Multiclass Classification
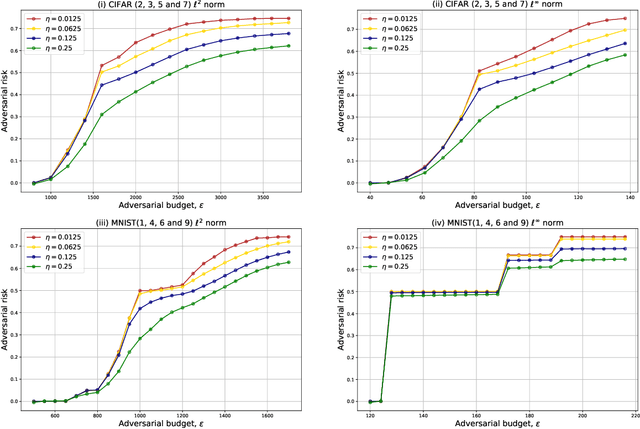
Jan 17, 2024Abstract:Despite the success of deep learning-based algorithms, it is widely known that neural networks may fail to be robust. A popular paradigm to enforce robustness is adversarial training (AT), however, this introduces many computational and theoretical difficulties. Recent works have developed a connection between AT in the multiclass classification setting and multimarginal optimal transport (MOT), unlocking a new set of tools to study this problem. In this paper, we leverage the MOT connection to propose computationally tractable numerical algorithms for computing universal lower bounds on the optimal adversarial risk and identifying optimal classifiers. We propose two main algorithms based on linear programming (LP) and entropic regularization (Sinkhorn). Our key insight is that one can harmlessly truncate the higher order interactions between classes, preventing the combinatorial run times typically encountered in MOT problems. We validate these results with experiments on MNIST and CIFAR-$10$, which demonstrate the tractability of our approach.
A New Perspective On Denoising Based On Optimal Transport
Dec 13, 2023Abstract:In the standard formulation of the denoising problem, one is given a probabilistic model relating a latent variable $\Theta \in \Omega \subset \mathbb{R}^m \; (m\ge 1)$ and an observation $Z \in \mathbb{R}^d$ according to: $Z \mid \Theta \sim p(\cdot\mid \Theta)$ and $\Theta \sim G^*$, and the goal is to construct a map to recover the latent variable from the observation. The posterior mean, a natural candidate for estimating $\Theta$ from $Z$, attains the minimum Bayes risk (under the squared error loss) but at the expense of over-shrinking the $Z$, and in general may fail to capture the geometric features of the prior distribution $G^*$ (e.g., low dimensionality, discreteness, sparsity, etc.). To rectify these drawbacks, in this paper we take a new perspective on this denoising problem that is inspired by optimal transport (OT) theory and use it to propose a new OT-based denoiser at the population level setting. We rigorously prove that, under general assumptions on the model, our OT-based denoiser is well-defined and unique, and is closely connected to solutions to a Monge OT problem. We then prove that, under appropriate identifiability assumptions on the model, our OT-based denoiser can be recovered solely from information of the marginal distribution of $Z$ and the posterior mean of the model, after solving a linear relaxation problem over a suitable space of couplings that is reminiscent of a standard multimarginal OT (MOT) problem. In particular, thanks to Tweedie's formula, when the likelihood model $\{ p(\cdot \mid \theta) \}_{\theta \in \Omega}$ is an exponential family of distributions, the OT-based denoiser can be recovered solely from the marginal distribution of $Z$. In general, our family of OT-like relaxations is of interest in its own right and for the denoising problem suggests alternative numerical methods inspired by the rich literature on computational OT.
Spectral Neural Networks: Approximation Theory and Optimization Landscape
Oct 01, 2023
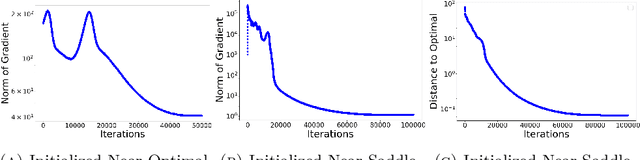
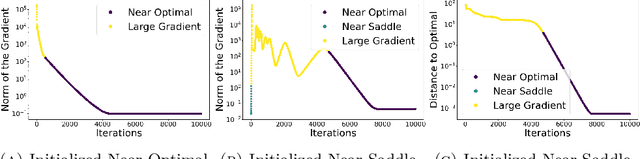
Abstract:There is a large variety of machine learning methodologies that are based on the extraction of spectral geometric information from data. However, the implementations of many of these methods often depend on traditional eigensolvers, which present limitations when applied in practical online big data scenarios. To address some of these challenges, researchers have proposed different strategies for training neural networks as alternatives to traditional eigensolvers, with one such approach known as Spectral Neural Network (SNN). In this paper, we investigate key theoretical aspects of SNN. First, we present quantitative insights into the tradeoff between the number of neurons and the amount of spectral geometric information a neural network learns. Second, we initiate a theoretical exploration of the optimization landscape of SNN's objective to shed light on the training dynamics of SNN. Unlike typical studies of convergence to global solutions of NN training dynamics, SNN presents an additional complexity due to its non-convex ambient loss function.
Continuum Limits of Ollivier's Ricci Curvature on data clouds: pointwise consistency and global lower bounds
Jul 05, 2023Abstract:Let $\mathcal{M} \subseteq \mathbb{R}^d$ denote a low-dimensional manifold and let $\mathcal{X}= \{ x_1, \dots, x_n \}$ be a collection of points uniformly sampled from $\mathcal{M}$. We study the relationship between the curvature of a random geometric graph built from $\mathcal{X}$ and the curvature of the manifold $\mathcal{M}$ via continuum limits of Ollivier's discrete Ricci curvature. We prove pointwise, non-asymptotic consistency results and also show that if $\mathcal{M}$ has Ricci curvature bounded from below by a positive constant, then the random geometric graph will inherit this global structural property with high probability. We discuss applications of the global discrete curvature bounds to contraction properties of heat kernels on graphs, as well as implications for manifold learning from data clouds. In particular, we show that the consistency results allow for characterizing the intrinsic curvature of a manifold from extrinsic curvature.
FedCBO: Reaching Group Consensus in Clustered Federated Learning through Consensus-based Optimization
May 04, 2023



Abstract:Federated learning is an important framework in modern machine learning that seeks to integrate the training of learning models from multiple users, each user having their own local data set, in a way that is sensitive to data privacy and to communication loss constraints. In clustered federated learning, one assumes an additional unknown group structure among users, and the goal is to train models that are useful for each group, rather than simply training a single global model for all users. In this paper, we propose a novel solution to the problem of clustered federated learning that is inspired by ideas in consensus-based optimization (CBO). Our new CBO-type method is based on a system of interacting particles that is oblivious to group memberships. Our model is motivated by rigorous mathematical reasoning, including a mean field analysis describing the large number of particles limit of our particle system, as well as convergence guarantees for the simultaneous global optimization of general non-convex objective functions (corresponding to the loss functions of each cluster of users) in the mean-field regime. Experimental results demonstrate the efficacy of our FedCBO algorithm compared to other state-of-the-art methods and help validate our methodological and theoretical work.
On the existence of solutions to adversarial training in multiclass classification
Apr 28, 2023Abstract:We study three models of the problem of adversarial training in multiclass classification designed to construct robust classifiers against adversarial perturbations of data in the agnostic-classifier setting. We prove the existence of Borel measurable robust classifiers in each model and provide a unified perspective of the adversarial training problem, expanding the connections with optimal transport initiated by the authors in previous work and developing new connections between adversarial training in the multiclass setting and total variation regularization. As a corollary of our results, we prove the existence of Borel measurable solutions to the agnostic adversarial training problem in the binary classification setting, a result that improves results in the literature of adversarial training, where robust classifiers were only known to exist within the enlarged universal $\sigma$-algebra of the feature space.
On adversarial robustness and the use of Wasserstein ascent-descent dynamics to enforce it
Jan 09, 2023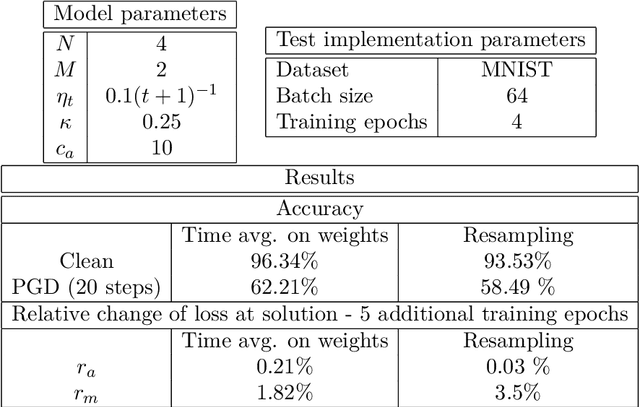
Abstract:We propose iterative algorithms to solve adversarial problems in a variety of supervised learning settings of interest. Our algorithms, which can be interpreted as suitable ascent-descent dynamics in Wasserstein spaces, take the form of a system of interacting particles. These interacting particle dynamics are shown to converge toward appropriate mean-field limit equations in certain large number of particles regimes. In turn, we prove that, under certain regularity assumptions, these mean-field equations converge, in the large time limit, toward approximate Nash equilibria of the original adversarial learning problems. We present results for nonconvex-nonconcave settings, as well as for nonconvex-concave ones. Numerical experiments illustrate our results.
Nonconvex Matrix Factorization is Geodesically Convex: Global Landscape Analysis for Fixed-rank Matrix Optimization From a Riemannian Perspective
Sep 29, 2022Abstract:We study a general matrix optimization problem with a fixed-rank positive semidefinite (PSD) constraint. We perform the Burer-Monteiro factorization and consider a particular Riemannian quotient geometry in a search space that has a total space equipped with the Euclidean metric. When the original objective f satisfies standard restricted strong convexity and smoothness properties, we characterize the global landscape of the factorized objective under the Riemannian quotient geometry. We show the entire search space can be divided into three regions: (R1) the region near the target parameter of interest, where the factorized objective is geodesically strongly convex and smooth; (R2) the region containing neighborhoods of all strict saddle points; (R3) the remaining regions, where the factorized objective has a large gradient. To our best knowledge, this is the first global landscape analysis of the Burer-Monteiro factorized objective under the Riemannian quotient geometry. Our results provide a fully geometric explanation for the superior performance of vanilla gradient descent under the Burer-Monteiro factorization. When f satisfies a weaker restricted strict convexity property, we show there exists a neighborhood near local minimizers such that the factorized objective is geodesically convex. To prove our results we provide a comprehensive landscape analysis of a matrix factorization problem with a least squares objective, which serves as a critical bridge. Our conclusions are also based on a result of independent interest stating that the geodesic ball centered at Y with a radius 1/3 of the least singular value of Y is a geodesically convex set under the Riemannian quotient geometry, which as a corollary, also implies a quantitative bound of the convexity radius in the Bures-Wasserstein space. The convexity radius obtained is sharp up to constants.
The Multimarginal Optimal Transport Formulation of Adversarial Multiclass Classification
Apr 27, 2022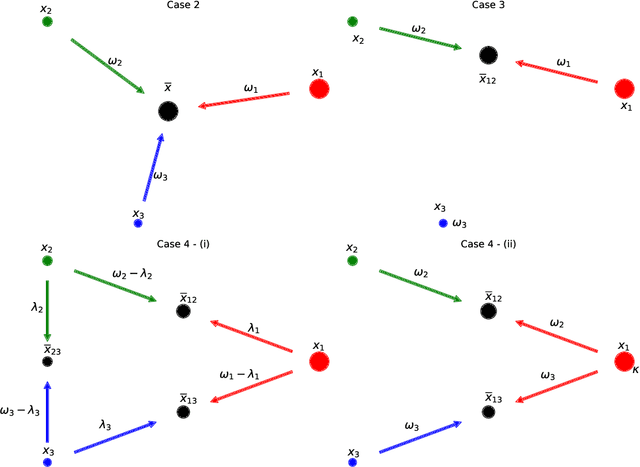
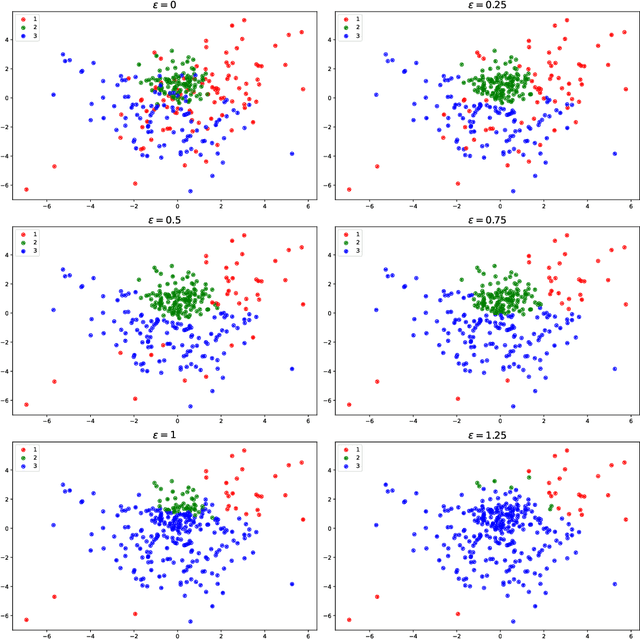
Abstract:We study a family of adversarial multiclass classification problems and provide equivalent reformulations in terms of: 1) a family of generalized barycenter problems introduced in the paper and 2) a family of multimarginal optimal transport problems where the number of marginals is equal to the number of classes in the original classification problem. These new theoretical results reveal a rich geometric structure of adversarial learning problems in multiclass classification and extend recent results restricted to the binary classification setting. A direct computational implication of our results is that by solving either the barycenter problem and its dual, or the MOT problem and its dual, we can recover the optimal robust classification rule and the optimal adversarial strategy for the original adversarial problem. Examples with synthetic and real data illustrate our results.
On the regularized risk of distributionally robust learning over deep neural networks
Sep 13, 2021
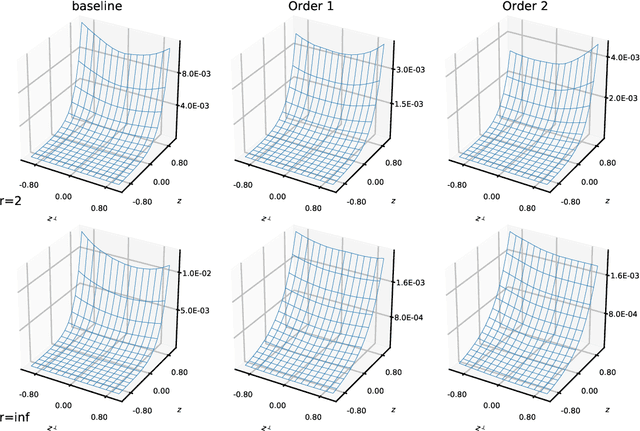
Abstract:In this paper we explore the relation between distributionally robust learning and different forms of regularization to enforce robustness of deep neural networks. In particular, starting from a concrete min-max distributionally robust problem, and using tools from optimal transport theory, we derive first order and second order approximations to the distributionally robust problem in terms of appropriate regularized risk minimization problems. In the context of deep ResNet models, we identify the structure of the resulting regularization problems as mean-field optimal control problems where the number and dimension of state variables is within a dimension-free factor of the dimension of the original unrobust problem. Using the Pontryagin maximum principles associated to these problems we motivate a family of scalable algorithms for the training of robust neural networks. Our analysis recovers some results and algorithms known in the literature (in settings explained throughout the paper) and provides many other theoretical and algorithmic insights that to our knowledge are novel. In our analysis we employ tools that we deem useful for a future analysis of more general adversarial learning problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge