Defending Against Diverse Attacks in Federated Learning Through Consensus-Based Bi-Level Optimization

Adversarial attacks pose significant challenges in many machine learning applications, particularly in the setting of distributed training and federated learning, where malicious agents seek to corrupt the training process with the goal of jeopardizing and compromising the performance and reliability of the final models. In this paper, we address the problem of robust federated learning in the presence of such attacks by formulating the training task as a bi-level optimization problem. We conduct a theoretical analysis of the resilience of consensus-based bi-level optimization (CB$^2$O), an interacting multi-particle metaheuristic optimization method, in adversarial settings. Specifically, we provide a global convergence analysis of CB$^2$O in mean-field law in the presence of malicious agents, demonstrating the robustness of CB$^2$O against a diverse range of attacks. Thereby, we offer insights into how specific hyperparameter choices enable to mitigate adversarial effects. On the practical side, we extend CB$^2$O to the clustered federated learning setting by proposing FedCB$^2$O, a novel interacting multi-particle system, and design a practical algorithm that addresses the demands of real-world applications. Extensive experiments demonstrate the robustness of the FedCB$^2$O algorithm against label-flipping attacks in decentralized clustered federated learning scenarios, showcasing its effectiveness in practical contexts.

On Bellman equations for continuous-time policy evaluation I: discretization and approximation

We study the problem of computing the value function from a discretely-observed trajectory of a continuous-time diffusion process. We develop a new class of algorithms based on easily implementable numerical schemes that are compatible with discrete-time reinforcement learning (RL) with function approximation. We establish high-order numerical accuracy as well as the approximation error guarantees for the proposed approach. In contrast to discrete-time RL problems where the approximation factor depends on the effective horizon, we obtain a bounded approximation factor using the underlying elliptic structures, even if the effective horizon diverges to infinity.

FedCBO: Reaching Group Consensus in Clustered Federated Learning through Consensus-based Optimization

Federated learning is an important framework in modern machine learning that seeks to integrate the training of learning models from multiple users, each user having their own local data set, in a way that is sensitive to data privacy and to communication loss constraints. In clustered federated learning, one assumes an additional unknown group structure among users, and the goal is to train models that are useful for each group, rather than simply training a single global model for all users. In this paper, we propose a novel solution to the problem of clustered federated learning that is inspired by ideas in consensus-based optimization (CBO). Our new CBO-type method is based on a system of interacting particles that is oblivious to group memberships. Our model is motivated by rigorous mathematical reasoning, including a mean field analysis describing the large number of particles limit of our particle system, as well as convergence guarantees for the simultaneous global optimization of general non-convex objective functions (corresponding to the loss functions of each cluster of users) in the mean-field regime. Experimental results demonstrate the efficacy of our FedCBO algorithm compared to other state-of-the-art methods and help validate our methodological and theoretical work.

Continuous-in-time Limit for Bayesian Bandits

This paper revisits the bandit problem in the Bayesian setting. The Bayesian approach formulates the bandit problem as an optimization problem, and the goal is to find the optimal policy which minimizes the Bayesian regret. One of the main challenges facing the Bayesian approach is that computation of the optimal policy is often intractable, especially when the length of the problem horizon or the number of arms is large. In this paper, we first show that under a suitable rescaling, the Bayesian bandit problem converges to a continuous Hamilton-Jacobi-Bellman (HJB) equation. The optimal policy for the limiting HJB equation can be explicitly obtained for several common bandit problems, and we give numerical methods to solve the HJB equation when an explicit solution is not available. Based on these results, we propose an approximate Bayes-optimal policy for solving Bayesian bandit problems with large horizons. Our method has the added benefit that its computational cost does not increase as the horizon increases.

On Large Batch Training and Sharp Minima: A Fokker-Planck Perspective

We study the statistical properties of the dynamic trajectory of stochastic gradient descent (SGD). We approximate the mini-batch SGD and the momentum SGD as stochastic differential equations (SDEs). We exploit the continuous formulation of SDE and the theory of Fokker-Planck equations to develop new results on the escaping phenomenon and the relationship with large batch and sharp minima. In particular, we find that the stochastic process solution tends to converge to flatter minima regardless of the batch size in the asymptotic regime. However, the convergence rate is rigorously proven to depend on the batch size. These results are validated empirically with various datasets and models.

Operator Augmentation for Model-based Policy Evaluation

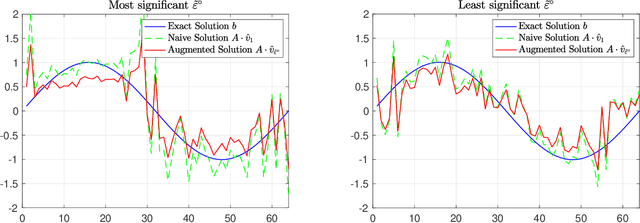
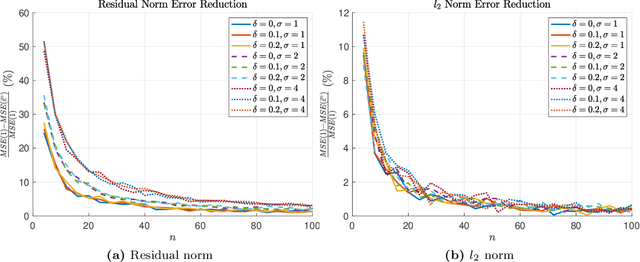
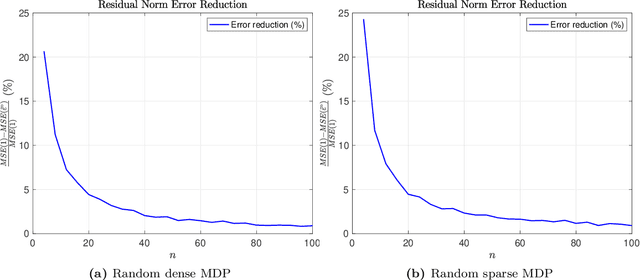
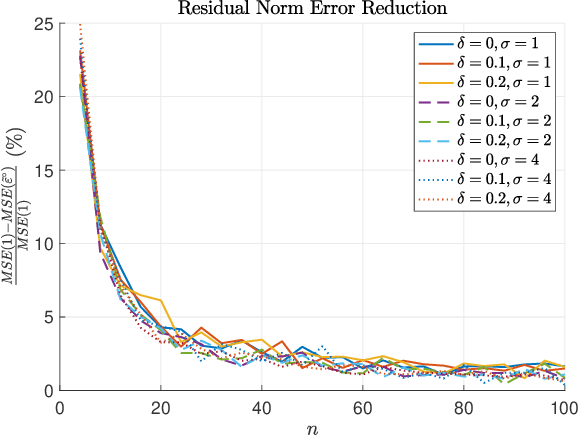
In model-based reinforcement learning, the transition matrix and reward vector are often estimated from random samples subject to noise. Even if the estimated model is an unbiased estimate of the true underlying model, the value function computed from the estimated model is biased. We introduce an operator augmentation method for reducing the error introduced by the estimated model. When the error is in the residual norm, we prove that the augmentation factor is always positive and upper bounded by $1 + O (1/n)$, where n is the number of samples used in learning each row of the transition matrix. We also propose a practical numerical algorithm for implementing the operator augmentation.

Variational Actor-Critic Algorithms

We introduce a class of variational actor-critic algorithms based on a variational formulation over both the value function and the policy. The objective function of the variational formulation consists of two parts: one for maximizing the value function and the other for minimizing the Bellman residual. Besides the vanilla gradient descent with both the value function and the policy updates, we propose two variants, the clipping method and the flipping method, in order to speed up the convergence. We also prove that, when the prefactor of the Bellman residual is sufficiently large, the fixed point of the algorithm is close to the optimal policy.

Why resampling outperforms reweighting for correcting sampling bias

A data set sampled from a certain population is biased if the subgroups of the population are sampled at proportions that are significantly different from their underlying proportions. Training machine learning models on biased data sets requires correction techniques to compensate for potential biases. We consider two commonly-used techniques, resampling and reweighting, that rebalance the proportions of the subgroups to maintain the desired objective function. Though statistically equivalent, it has been observed that reweighting outperforms resampling when combined with stochastic gradient algorithms. By analyzing illustrative examples, we explain the reason behind this phenomenon using tools from dynamical stability and stochastic asymptotics. We also present experiments from regression, classification, and off-policy prediction to demonstrate that this is a general phenomenon. We argue that it is imperative to consider the objective function design and the optimization algorithm together while addressing the sampling bias.

Borrowing From the Future: Addressing Double Sampling in Model-free Control

In model-free reinforcement learning, the temporal difference method and its variants become unstable when combined with nonlinear function approximations. Bellman residual minimization with stochastic gradient descent (SGD) is more stable, but it suffers from the double sampling problem: given the current state, two independent samples for the next state are required, but often only one sample is available. Recently, the authors of [Zhu et al, 2020] introduced the borrowing from the future (BFF) algorithm to address this issue for the prediction problem. The main idea is to borrow extra randomness from the future to approximately re-sample the next state when the underlying dynamics of the problem are sufficiently smooth. This paper extends the BFF algorithm to action-value function based model-free control. We prove that BFF is close to unbiased SGD when the underlying dynamics vary slowly with respect to actions. We confirm our theoretical findings with numerical simulations.

Towards Theoretical Understanding of Large Batch Training in Stochastic Gradient Descent

Stochastic gradient descent (SGD) is almost ubiquitously used for training non-convex optimization tasks. Recently, a hypothesis proposed by Keskar et al. [2017] that large batch methods tend to converge to sharp minimizers has received increasing attention. We theoretically justify this hypothesis by providing new properties of SGD in both finite-time and asymptotic regimes. In particular, we give an explicit escaping time of SGD from a local minimum in the finite-time regime and prove that SGD tends to converge to flatter minima in the asymptotic regime (although may take exponential time to converge) regardless of the batch size. We also find that SGD with a larger ratio of learning rate to batch size tends to converge to a flat minimum faster, however, its generalization performance could be worse than the SGD with a smaller ratio of learning rate to batch size. We include numerical experiments to corroborate these theoretical findings.