Continuous-in-time Limit for Bayesian Bandits

This paper revisits the bandit problem in the Bayesian setting. The Bayesian approach formulates the bandit problem as an optimization problem, and the goal is to find the optimal policy which minimizes the Bayesian regret. One of the main challenges facing the Bayesian approach is that computation of the optimal policy is often intractable, especially when the length of the problem horizon or the number of arms is large. In this paper, we first show that under a suitable rescaling, the Bayesian bandit problem converges to a continuous Hamilton-Jacobi-Bellman (HJB) equation. The optimal policy for the limiting HJB equation can be explicitly obtained for several common bandit problems, and we give numerical methods to solve the HJB equation when an explicit solution is not available. Based on these results, we propose an approximate Bayes-optimal policy for solving Bayesian bandit problems with large horizons. Our method has the added benefit that its computational cost does not increase as the horizon increases.

Borrowing From the Future: Addressing Double Sampling in Model-free Control

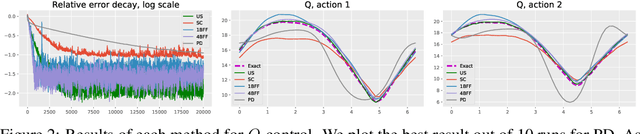
In model-free reinforcement learning, the temporal difference method and its variants become unstable when combined with nonlinear function approximations. Bellman residual minimization with stochastic gradient descent (SGD) is more stable, but it suffers from the double sampling problem: given the current state, two independent samples for the next state are required, but often only one sample is available. Recently, the authors of [Zhu et al, 2020] introduced the borrowing from the future (BFF) algorithm to address this issue for the prediction problem. The main idea is to borrow extra randomness from the future to approximately re-sample the next state when the underlying dynamics of the problem are sufficiently smooth. This paper extends the BFF algorithm to action-value function based model-free control. We prove that BFF is close to unbiased SGD when the underlying dynamics vary slowly with respect to actions. We confirm our theoretical findings with numerical simulations.