HyperDPO: Hypernetwork-based Multi-Objective Fine-Tuning Framework

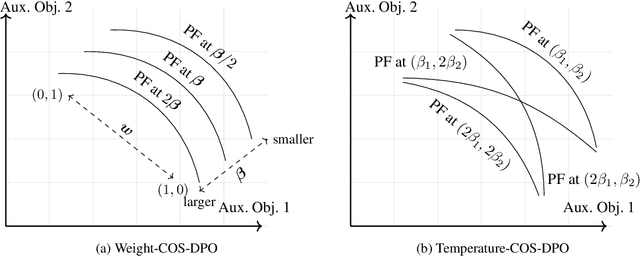
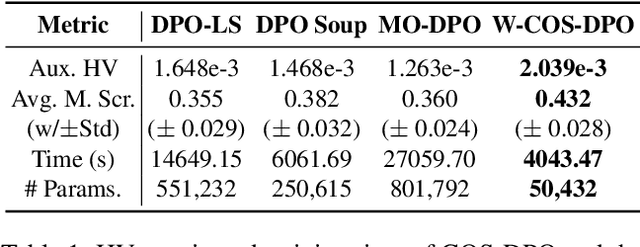
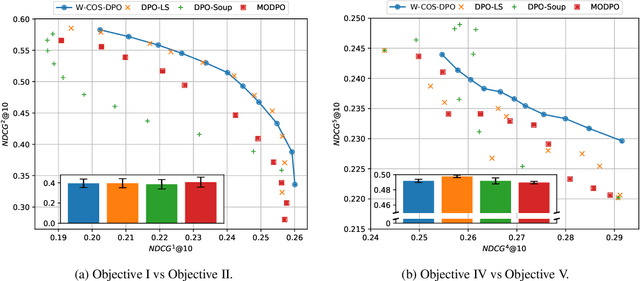
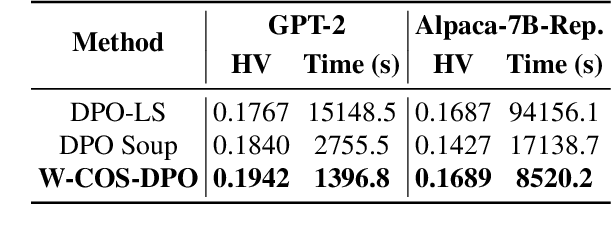
In LLM alignment and many other ML applications, one often faces the Multi-Objective Fine-Tuning (MOFT) problem, i.e. fine-tuning an existing model with datasets labeled w.r.t. different objectives simultaneously. To address the challenge, we propose the HyperDPO framework, a hypernetwork-based approach that extends the Direct Preference Optimization (DPO) technique, originally developed for efficient LLM alignment with preference data, to accommodate the MOFT settings. By substituting the Bradley-Terry-Luce model in DPO with the Plackett-Luce model, our framework is capable of handling a wide range of MOFT tasks that involve listwise ranking datasets. Compared with previous approaches, HyperDPO enjoys an efficient one-shot training process for profiling the Pareto front of auxiliary objectives, and offers flexible post-training control over trade-offs. Additionally, we propose a novel Hyper Prompt Tuning design, that conveys continuous weight across objectives to transformer-based models without altering their architecture. We demonstrate the effectiveness and efficiency of the HyperDPO framework through its applications to various tasks, including Learning-to-Rank (LTR) and LLM alignment, highlighting its viability for large-scale ML deployments.

How Discrete and Continuous Diffusion Meet: Comprehensive Analysis of Discrete Diffusion Models via a Stochastic Integral Framework

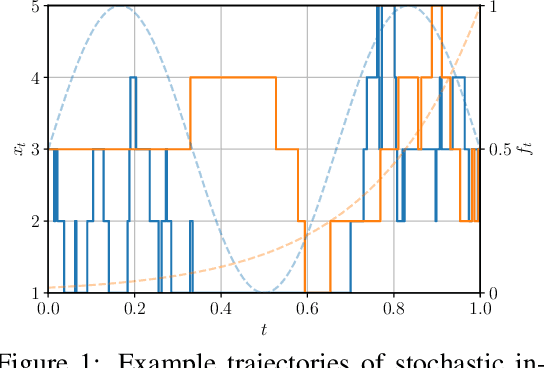
Discrete diffusion models have gained increasing attention for their ability to model complex distributions with tractable sampling and inference. However, the error analysis for discrete diffusion models remains less well-understood. In this work, we propose a comprehensive framework for the error analysis of discrete diffusion models based on L\'evy-type stochastic integrals. By generalizing the Poisson random measure to that with a time-independent and state-dependent intensity, we rigorously establish a stochastic integral formulation of discrete diffusion models and provide the corresponding change of measure theorems that are intriguingly analogous to It\^o integrals and Girsanov's theorem for their continuous counterparts. Our framework unifies and strengthens the current theoretical results on discrete diffusion models and obtains the first error bound for the $\tau$-leaping scheme in KL divergence. With error sources clearly identified, our analysis gives new insight into the mathematical properties of discrete diffusion models and offers guidance for the design of efficient and accurate algorithms for real-world discrete diffusion model applications.

Tangent differential privacy

Differential privacy is a framework for protecting the identity of individual data points in the decision-making process. In this note, we propose a new form of differential privacy called tangent differential privacy. Compared with the usual differential privacy that is defined uniformly across data distributions, tangent differential privacy is tailored towards a specific data distribution of interest. It also allows for general distribution distances such as total variation distance and Wasserstein distance. In the case of risk minimization, we show that entropic regularization guarantees tangent differential privacy under rather general conditions on the risk function.

Accelerating Diffusion Models with Parallel Sampling: Inference at Sub-Linear Time Complexity

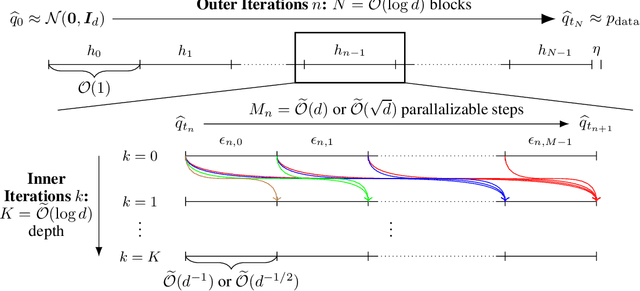
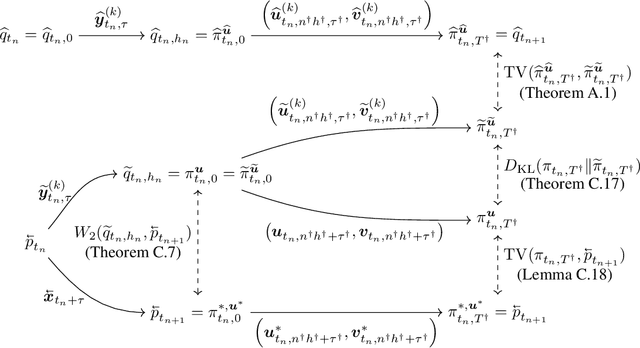
Diffusion models have become a leading method for generative modeling of both image and scientific data. As these models are costly to train and evaluate, reducing the inference cost for diffusion models remains a major goal. Inspired by the recent empirical success in accelerating diffusion models via the parallel sampling technique~\cite{shih2024parallel}, we propose to divide the sampling process into $\mathcal{O}(1)$ blocks with parallelizable Picard iterations within each block. Rigorous theoretical analysis reveals that our algorithm achieves $\widetilde{\mathcal{O}}(\mathrm{poly} \log d)$ overall time complexity, marking the first implementation with provable sub-linear complexity w.r.t. the data dimension $d$. Our analysis is based on a generalized version of Girsanov's theorem and is compatible with both the SDE and probability flow ODE implementations. Our results shed light on the potential of fast and efficient sampling of high-dimensional data on fast-evolving modern large-memory GPU clusters.

A note on continuous-time online learning

In online learning, the data is provided in a sequential order, and the goal of the learner is to make online decisions to minimize overall regrets. This note is concerned with continuous-time models and algorithms for several online learning problems: online linear optimization, adversarial bandit, and adversarial linear bandit. For each problem, we extend the discrete-time algorithm to the continuous-time setting and provide a concise proof of the optimal regret bound.

Orthogonal Bootstrap: Efficient Simulation of Input Uncertainty

Bootstrap is a popular methodology for simulating input uncertainty. However, it can be computationally expensive when the number of samples is large. We propose a new approach called \textbf{Orthogonal Bootstrap} that reduces the number of required Monte Carlo replications. We decomposes the target being simulated into two parts: the \textit{non-orthogonal part} which has a closed-form result known as Infinitesimal Jackknife and the \textit{orthogonal part} which is easier to be simulated. We theoretically and numerically show that Orthogonal Bootstrap significantly reduces the computational cost of Bootstrap while improving empirical accuracy and maintaining the same width of the constructed interval.

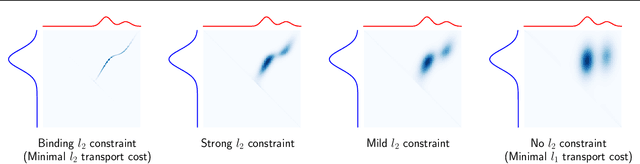
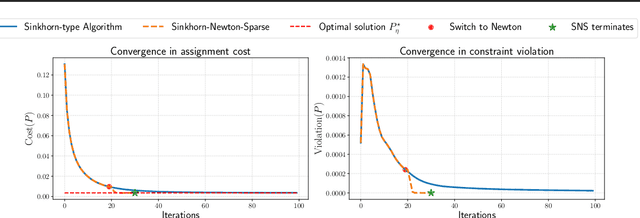
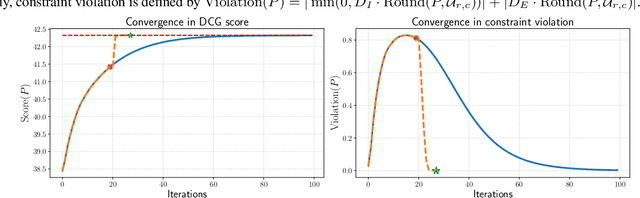
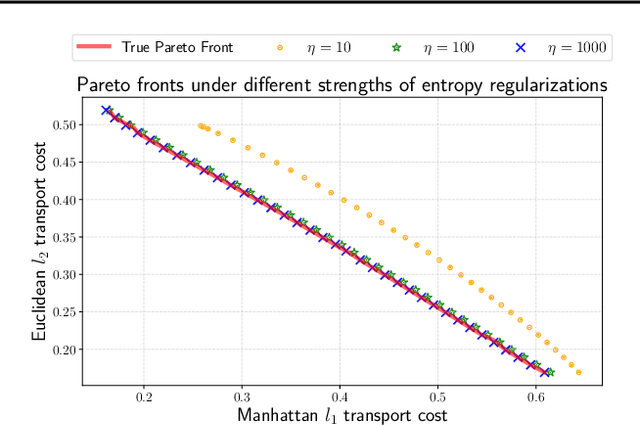
A Sinkhorn-type Algorithm for Constrained Optimal Transport

Entropic optimal transport (OT) and the Sinkhorn algorithm have made it practical for machine learning practitioners to perform the fundamental task of calculating transport distance between statistical distributions. In this work, we focus on a general class of OT problems under a combination of equality and inequality constraints. We derive the corresponding entropy regularization formulation and introduce a Sinkhorn-type algorithm for such constrained OT problems supported by theoretical guarantees. We first bound the approximation error when solving the problem through entropic regularization, which reduces exponentially with the increase of the regularization parameter. Furthermore, we prove a sublinear first-order convergence rate of the proposed Sinkhorn-type algorithm in the dual space by characterizing the optimization procedure with a Lyapunov function. To achieve fast and higher-order convergence under weak entropy regularization, we augment the Sinkhorn-type algorithm with dynamic regularization scheduling and second-order acceleration. Overall, this work systematically combines recent theoretical and numerical advances in entropic optimal transport with the constrained case, allowing practitioners to derive approximate transport plans in complex scenarios.

Multidimensional unstructured sparse recovery via eigenmatrix

This note considers the multidimensional unstructured sparse recovery problems. Examples include Fourier inversion and sparse deconvolution. The eigenmatrix is a data-driven construction with desired approximate eigenvalues and eigenvectors proposed for the one-dimensional problems. This note extends the eigenmatrix approach to multidimensional problems. Numerical results are provided to demonstrate the performance of the proposed method.

Convergence Analysis of Discrete Diffusion Model: Exact Implementation through Uniformization

Diffusion models have achieved huge empirical success in data generation tasks. Recently, some efforts have been made to adapt the framework of diffusion models to discrete state space, providing a more natural approach for modeling intrinsically discrete data, such as language and graphs. This is achieved by formulating both the forward noising process and the corresponding reversed process as Continuous Time Markov Chains (CTMCs). In this paper, we investigate the theoretical properties of the discrete diffusion model. Specifically, we introduce an algorithm leveraging the uniformization of continuous Markov chains, implementing transitions on random time points. Under reasonable assumptions on the learning of the discrete score function, we derive Total Variation distance and KL divergence guarantees for sampling from any distribution on a hypercube. Our results align with state-of-the-art achievements for diffusion models in $\mathbb{R}^d$ and further underscore the advantages of discrete diffusion models in comparison to the $\mathbb{R}^d$ setting.

Ensemble-Based Annealed Importance Sampling

Sampling from a multimodal distribution is a fundamental and challenging problem in computational science and statistics. Among various approaches proposed for this task, one popular method is Annealed Importance Sampling (AIS). In this paper, we propose an ensemble-based version of AIS by combining it with population-based Monte Carlo methods to improve its efficiency. By keeping track of an ensemble instead of a single particle along some continuation path between the starting distribution and the target distribution, we take advantage of the interaction within the ensemble to encourage the exploration of undiscovered modes. Specifically, our main idea is to utilize either the snooker algorithm or the genetic algorithm used in Evolutionary Monte Carlo. We discuss how the proposed algorithm can be implemented and derive a partial differential equation governing the evolution of the ensemble under the continuous time and mean-field limit. We also test the efficiency of the proposed algorithm on various continuous and discrete distributions.