A Sinkhorn-type Algorithm for Constrained Optimal Transport
Paper and Code
Mar 08, 2024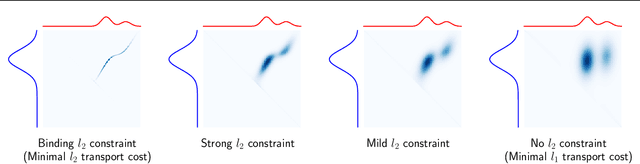
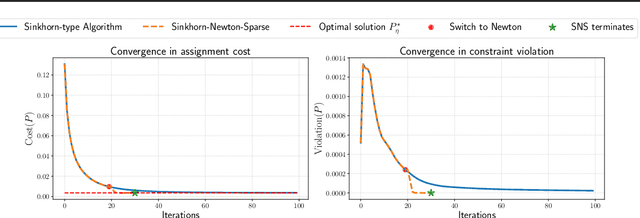
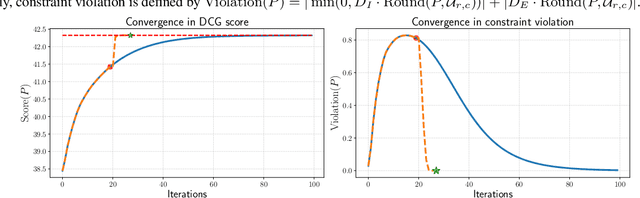
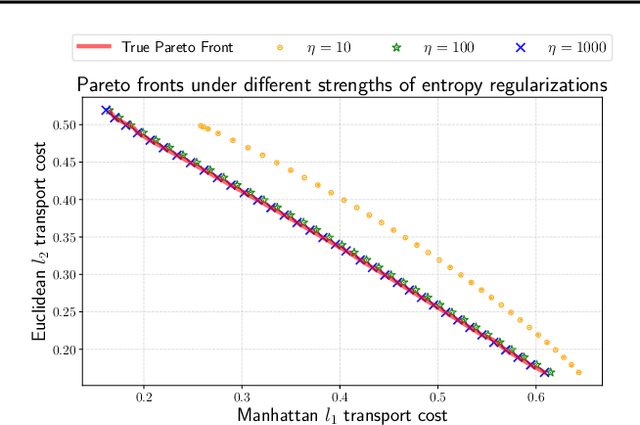
Entropic optimal transport (OT) and the Sinkhorn algorithm have made it practical for machine learning practitioners to perform the fundamental task of calculating transport distance between statistical distributions. In this work, we focus on a general class of OT problems under a combination of equality and inequality constraints. We derive the corresponding entropy regularization formulation and introduce a Sinkhorn-type algorithm for such constrained OT problems supported by theoretical guarantees. We first bound the approximation error when solving the problem through entropic regularization, which reduces exponentially with the increase of the regularization parameter. Furthermore, we prove a sublinear first-order convergence rate of the proposed Sinkhorn-type algorithm in the dual space by characterizing the optimization procedure with a Lyapunov function. To achieve fast and higher-order convergence under weak entropy regularization, we augment the Sinkhorn-type algorithm with dynamic regularization scheduling and second-order acceleration. Overall, this work systematically combines recent theoretical and numerical advances in entropic optimal transport with the constrained case, allowing practitioners to derive approximate transport plans in complex scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge