Kiran Koshy Thekumparampil
RewardRank: Optimizing True Learning-to-Rank Utility
Aug 19, 2025
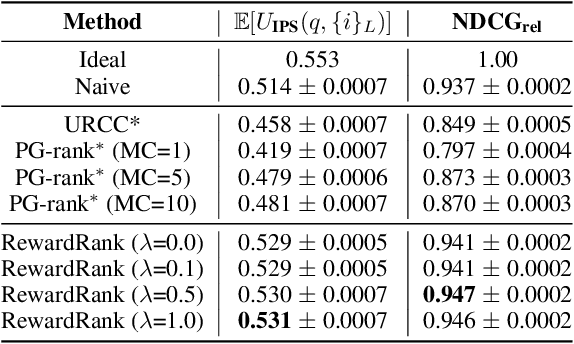
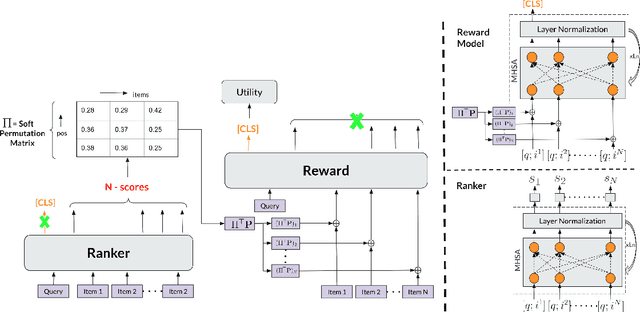
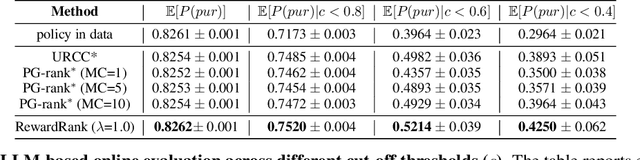
Abstract:Traditional ranking systems rely on proxy loss functions that assume simplistic user behavior, such as users preferring a rank list where items are sorted by hand-crafted relevance. However, real-world user interactions are influenced by complex behavioral biases, including position bias, brand affinity, decoy effects, and similarity aversion, which these objectives fail to capture. As a result, models trained on such losses often misalign with actual user utility, such as the probability of any click or purchase across the ranked list. In this work, we propose a data-driven framework for modeling user behavior through counterfactual reward learning. Our method, RewardRank, first trains a deep utility model to estimate user engagement for entire item permutations using logged data. Then, a ranking policy is optimized to maximize predicted utility via differentiable soft permutation operators, enabling end-to-end training over the space of factual and counterfactual rankings. To address the challenge of evaluation without ground-truth for unseen permutations, we introduce two automated protocols: (i) $\textit{KD-Eval}$, using a position-aware oracle for counterfactual reward estimation, and (ii) $\textit{LLM-Eval}$, which simulates user preferences via large language models. Experiments on large-scale benchmarks, including Baidu-ULTR and the Amazon KDD Cup datasets, demonstrate that our approach consistently outperforms strong baselines, highlighting the effectiveness of modeling user behavior dynamics for utility-optimized ranking. Our code is available at: https://github.com/GauravBh1010tt/RewardRank
Zeroth-Order Optimization Finds Flat Minima
Jun 05, 2025Abstract:Zeroth-order methods are extensively used in machine learning applications where gradients are infeasible or expensive to compute, such as black-box attacks, reinforcement learning, and language model fine-tuning. Existing optimization theory focuses on convergence to an arbitrary stationary point, but less is known on the implicit regularization that provides a fine-grained characterization on which particular solutions are finally reached. We show that zeroth-order optimization with the standard two-point estimator favors solutions with small trace of Hessian, which is widely used in previous work to distinguish between sharp and flat minima. We further provide convergence rates of zeroth-order optimization to approximate flat minima for convex and sufficiently smooth functions, where flat minima are defined as the minimizers that achieve the smallest trace of Hessian among all optimal solutions. Experiments on binary classification tasks with convex losses and language model fine-tuning support our theoretical findings.
Comparing Few to Rank Many: Active Human Preference Learning using Randomized Frank-Wolfe
Dec 27, 2024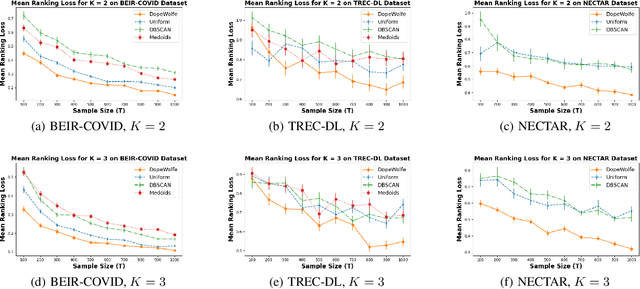

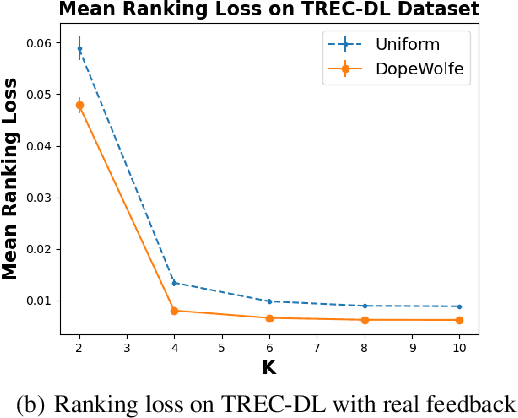
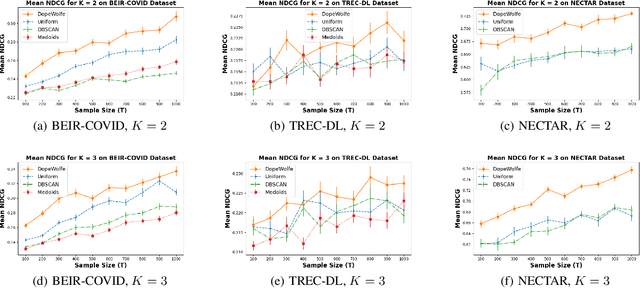
Abstract:We study learning of human preferences from a limited comparison feedback. This task is ubiquitous in machine learning. Its applications such as reinforcement learning from human feedback, have been transformational. We formulate this problem as learning a Plackett-Luce model over a universe of $N$ choices from $K$-way comparison feedback, where typically $K \ll N$. Our solution is the D-optimal design for the Plackett-Luce objective. The design defines a data logging policy that elicits comparison feedback for a small collection of optimally chosen points from all ${N \choose K}$ feasible subsets. The main algorithmic challenge in this work is that even fast methods for solving D-optimal designs would have $O({N \choose K})$ time complexity. To address this issue, we propose a randomized Frank-Wolfe (FW) algorithm that solves the linear maximization sub-problems in the FW method on randomly chosen variables. We analyze the algorithm, and evaluate it empirically on synthetic and open-source NLP datasets.
A Sinkhorn-type Algorithm for Constrained Optimal Transport
Mar 08, 2024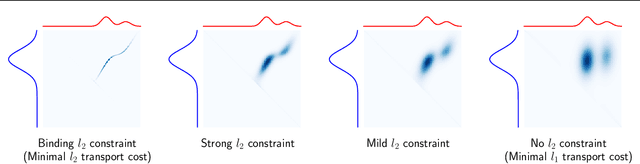
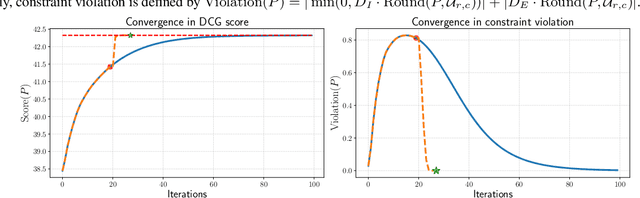
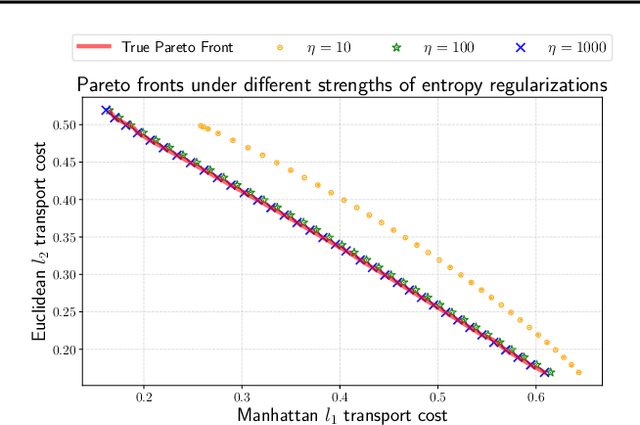
Abstract:Entropic optimal transport (OT) and the Sinkhorn algorithm have made it practical for machine learning practitioners to perform the fundamental task of calculating transport distance between statistical distributions. In this work, we focus on a general class of OT problems under a combination of equality and inequality constraints. We derive the corresponding entropy regularization formulation and introduce a Sinkhorn-type algorithm for such constrained OT problems supported by theoretical guarantees. We first bound the approximation error when solving the problem through entropic regularization, which reduces exponentially with the increase of the regularization parameter. Furthermore, we prove a sublinear first-order convergence rate of the proposed Sinkhorn-type algorithm in the dual space by characterizing the optimization procedure with a Lyapunov function. To achieve fast and higher-order convergence under weak entropy regularization, we augment the Sinkhorn-type algorithm with dynamic regularization scheduling and second-order acceleration. Overall, this work systematically combines recent theoretical and numerical advances in entropic optimal transport with the constrained case, allowing practitioners to derive approximate transport plans in complex scenarios.
Accelerating Sinkhorn Algorithm with Sparse Newton Iterations
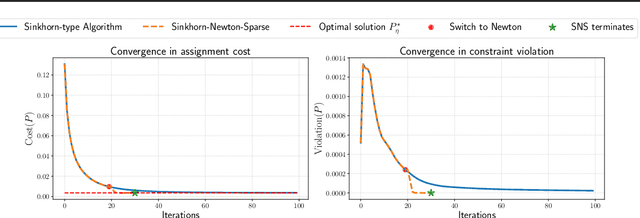
Jan 20, 2024Abstract:Computing the optimal transport distance between statistical distributions is a fundamental task in machine learning. One remarkable recent advancement is entropic regularization and the Sinkhorn algorithm, which utilizes only matrix scaling and guarantees an approximated solution with near-linear runtime. Despite the success of the Sinkhorn algorithm, its runtime may still be slow due to the potentially large number of iterations needed for convergence. To achieve possibly super-exponential convergence, we present Sinkhorn-Newton-Sparse (SNS), an extension to the Sinkhorn algorithm, by introducing early stopping for the matrix scaling steps and a second stage featuring a Newton-type subroutine. Adopting the variational viewpoint that the Sinkhorn algorithm maximizes a concave Lyapunov potential, we offer the insight that the Hessian matrix of the potential function is approximately sparse. Sparsification of the Hessian results in a fast $O(n^2)$ per-iteration complexity, the same as the Sinkhorn algorithm. In terms of total iteration count, we observe that the SNS algorithm converges orders of magnitude faster across a wide range of practical cases, including optimal transportation between empirical distributions and calculating the Wasserstein $W_1, W_2$ distance of discretized densities. The empirical performance is corroborated by a rigorous bound on the approximate sparsity of the Hessian matrix.
DPZero: Dimension-Independent and Differentially Private Zeroth-Order Optimization
Oct 14, 2023Abstract:The widespread practice of fine-tuning pretrained large language models (LLMs) on domain-specific data faces two major challenges in memory and privacy. First, as the size of LLMs continue to grow, encompassing billions of parameters, the memory demands of gradient-based training methods via backpropagation become prohibitively high. Second, given the tendency of LLMs to memorize and disclose sensitive training data, the privacy of fine-tuning data must be respected. To this end, we explore the potential of zeroth-order methods in differentially private optimization for fine-tuning LLMs. Zeroth-order methods, which rely solely on forward passes, substantially reduce memory consumption during training. However, directly combining them with standard differential privacy mechanism poses dimension-dependent complexity. To bridge the gap, we introduce DPZero, a novel differentially private zeroth-order algorithm with nearly dimension-independent rates. Our theoretical analysis reveals that its complexity hinges primarily on the problem's intrinsic dimension and exhibits only a logarithmic dependence on the ambient dimension. This renders DPZero a highly practical option for real-world LLMs deployments.
Pretrained deep models outperform GBDTs in Learning-To-Rank under label scarcity
Jul 31, 2023



Abstract:While deep learning (DL) models are state-of-the-art in text and image domains, they have not yet consistently outperformed Gradient Boosted Decision Trees (GBDTs) on tabular Learning-To-Rank (LTR) problems. Most of the recent performance gains attained by DL models in text and image tasks have used unsupervised pretraining, which exploits orders of magnitude more unlabeled data than labeled data. To the best of our knowledge, unsupervised pretraining has not been applied to the LTR problem, which often produces vast amounts of unlabeled data. In this work, we study whether unsupervised pretraining can improve LTR performance over GBDTs and other non-pretrained models. Using simple design choices--including SimCLR-Rank, our ranking-specific modification of SimCLR (an unsupervised pretraining method for images)--we produce pretrained deep learning models that soundly outperform GBDTs (and other non-pretrained models) in the case where labeled data is vastly outnumbered by unlabeled data. We also show that pretrained models also often achieve significantly better robustness than non-pretrained models (GBDTs or DL models) in ranking outlier data.
Bring Your Own Algorithm for Optimal Differentially Private Stochastic Minimax Optimization
Jun 01, 2022

Abstract:We study differentially private (DP) algorithms for smooth stochastic minimax optimization, with stochastic minimization as a byproduct. The holy grail of these settings is to guarantee the optimal trade-off between the privacy and the excess population loss, using an algorithm with a linear time-complexity in the number of training samples. We provide a general framework for solving differentially private stochastic minimax optimization (DP-SMO) problems, which enables the practitioners to bring their own base optimization algorithm and use it as a black-box to obtain the near-optimal privacy-loss trade-off. Our framework is inspired from the recently proposed Phased-ERM method [20] for nonsmooth differentially private stochastic convex optimization (DP-SCO), which exploits the stability of the empirical risk minimization (ERM) for the privacy guarantee. The flexibility of our approach enables us to sidestep the requirement that the base algorithm needs to have bounded sensitivity, and allows the use of sophisticated variance-reduced accelerated methods to achieve near-linear time-complexity. To the best of our knowledge, these are the first linear-time optimal algorithms, up to logarithmic factors, for smooth DP-SMO when the objective is (strongly-)convex-(strongly-)concave. Additionally, based on our flexible framework, we derive a new family of near-linear time algorithms for smooth DP-SCO with optimal privacy-loss trade-offs for a wider range of smoothness parameters compared to previous algorithms.
Lifted Primal-Dual Method for Bilinearly Coupled Smooth Minimax Optimization
Jan 19, 2022
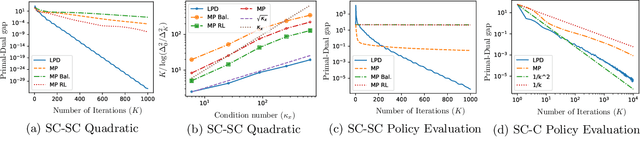
Abstract:We study the bilinearly coupled minimax problem: $\min_{x} \max_{y} f(x) + y^\top A x - h(y)$, where $f$ and $h$ are both strongly convex smooth functions and admit first-order gradient oracles. Surprisingly, no known first-order algorithms have hitherto achieved the lower complexity bound of $\Omega((\sqrt{\frac{L_x}{\mu_x}} + \frac{\|A\|}{\sqrt{\mu_x \mu_y}} + \sqrt{\frac{L_y}{\mu_y}}) \log(\frac1{\varepsilon}))$ for solving this problem up to an $\varepsilon$ primal-dual gap in the general parameter regime, where $L_x, L_y,\mu_x,\mu_y$ are the corresponding smoothness and strongly convexity constants. We close this gap by devising the first optimal algorithm, the Lifted Primal-Dual (LPD) method. Our method lifts the objective into an extended form that allows both the smooth terms and the bilinear term to be handled optimally and seamlessly with the same primal-dual framework. Besides optimality, our method yields a desirably simple single-loop algorithm that uses only one gradient oracle call per iteration. Moreover, when $f$ is just convex, the same algorithm applied to a smoothed objective achieves the nearly optimal iteration complexity. We also provide a direct single-loop algorithm, using the LPD method, that achieves the iteration complexity of $O(\sqrt{\frac{L_x}{\varepsilon}} + \frac{\|A\|}{\sqrt{\mu_y \varepsilon}} + \sqrt{\frac{L_y}{\varepsilon}})$. Numerical experiments on quadratic minimax problems and policy evaluation problems further demonstrate the fast convergence of our algorithm in practice.
Sample Efficient Linear Meta-Learning by Alternating Minimization
May 18, 2021
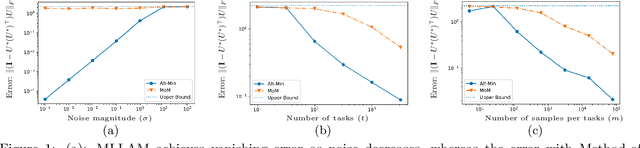
Abstract:Meta-learning synthesizes and leverages the knowledge from a given set of tasks to rapidly learn new tasks using very little data. Meta-learning of linear regression tasks, where the regressors lie in a low-dimensional subspace, is an extensively-studied fundamental problem in this domain. However, existing results either guarantee highly suboptimal estimation errors, or require $\Omega(d)$ samples per task (where $d$ is the data dimensionality) thus providing little gain over separately learning each task. In this work, we study a simple alternating minimization method (MLLAM), which alternately learns the low-dimensional subspace and the regressors. We show that, for a constant subspace dimension MLLAM obtains nearly-optimal estimation error, despite requiring only $\Omega(\log d)$ samples per task. However, the number of samples required per task grows logarithmically with the number of tasks. To remedy this in the low-noise regime, we propose a novel task subset selection scheme that ensures the same strong statistical guarantee as MLLAM, even with bounded number of samples per task for arbitrarily large number of tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge