Comparing Few to Rank Many: Active Human Preference Learning using Randomized Frank-Wolfe

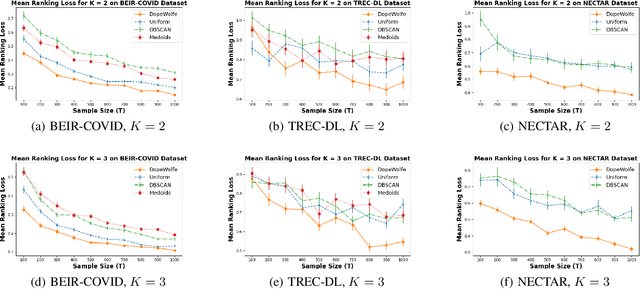
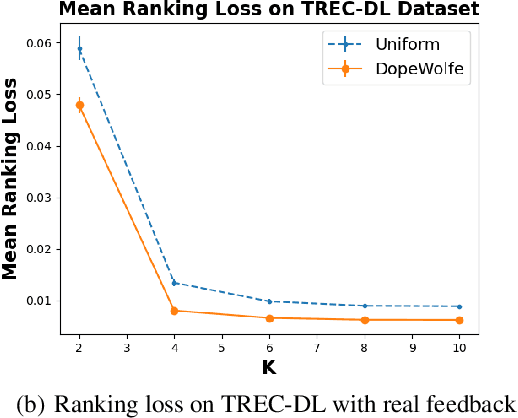
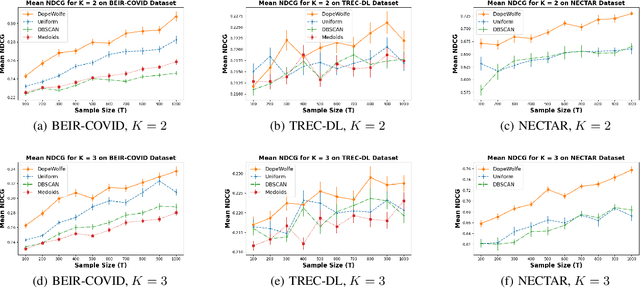
We study learning of human preferences from a limited comparison feedback. This task is ubiquitous in machine learning. Its applications such as reinforcement learning from human feedback, have been transformational. We formulate this problem as learning a Plackett-Luce model over a universe of $N$ choices from $K$-way comparison feedback, where typically $K \ll N$. Our solution is the D-optimal design for the Plackett-Luce objective. The design defines a data logging policy that elicits comparison feedback for a small collection of optimally chosen points from all ${N \choose K}$ feasible subsets. The main algorithmic challenge in this work is that even fast methods for solving D-optimal designs would have $O({N \choose K})$ time complexity. To address this issue, we propose a randomized Frank-Wolfe (FW) algorithm that solves the linear maximization sub-problems in the FW method on randomly chosen variables. We analyze the algorithm, and evaluate it empirically on synthetic and open-source NLP datasets.

Language-Model Prior Overcomes Cold-Start Items

The growth of recommender systems (RecSys) is driven by digitization and the need for personalized content in areas such as e-commerce and video streaming. The content in these systems often changes rapidly and therefore they constantly face the ongoing cold-start problem, where new items lack interaction data and are hard to value. Existing solutions for the cold-start problem, such as content-based recommenders and hybrid methods, leverage item metadata to determine item similarities. The main challenge with these methods is their reliance on structured and informative metadata to capture detailed item similarities, which may not always be available. This paper introduces a novel approach for cold-start item recommendation that utilizes the language model (LM) to estimate item similarities, which are further integrated as a Bayesian prior with classic recommender systems. This approach is generic and able to boost the performance of various recommenders. Specifically, our experiments integrate it with both sequential and collaborative filtering-based recommender and evaluate it on two real-world datasets, demonstrating the enhanced performance of the proposed approach.

Optimal Design for Human Feedback

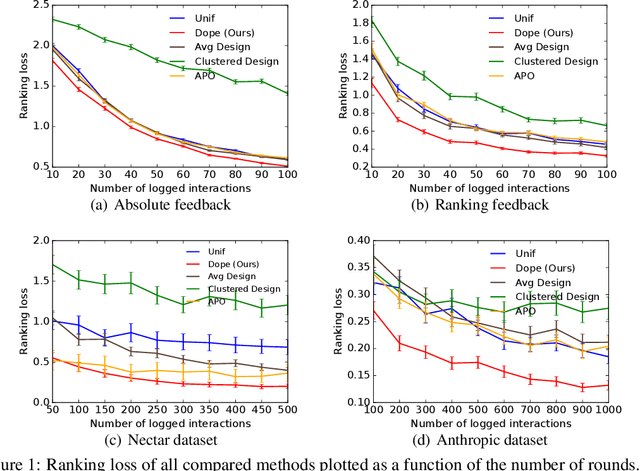
Learning of preference models from human feedback has been central to recent advances in artificial intelligence. Motivated by this progress, and the cost of obtaining high-quality human annotations, we study the problem of data collection for learning preference models. The key idea in our work is to generalize optimal designs, a tool for computing efficient data logging policies, to ranked lists. To show the generality of our ideas, we study both absolute and relative feedback on items in the list. We design efficient algorithms for both settings and analyze them. We prove that our preference model estimators improve with more data and so does the ranking error under the estimators. Finally, we experiment with several synthetic and real-world datasets to show the statistical efficiency of our algorithms.

Fixed-Budget Best-Arm Identification with Heterogeneous Reward Variances

We study the problem of best-arm identification (BAI) in the fixed-budget setting with heterogeneous reward variances. We propose two variance-adaptive BAI algorithms for this setting: SHVar for known reward variances and SHAdaVar for unknown reward variances. Our algorithms rely on non-uniform budget allocations among the arms where the arms with higher reward variances are pulled more often than those with lower variances. The main algorithmic novelty is in the design of SHAdaVar, which allocates budget greedily based on overestimating the unknown reward variances. We bound probabilities of misidentifying the best arms in both SHVar and SHAdaVar. Our analyses rely on novel lower bounds on the number of pulls of an arm that do not require closed-form solutions to the budget allocation problem. Since one of our budget allocation problems is analogous to the optimal experiment design with unknown variances, we believe that our results are of a broad interest. Our experiments validate our theory, and show that SHVar and SHAdaVar outperform algorithms from prior works with analytical guarantees.