Replicable Bandits with UCB based Exploration

We study replicable algorithms for stochastic multi-armed bandits (MAB) and linear bandits with UCB (Upper Confidence Bound) based exploration. A bandit algorithm is $ρ$-replicable if two executions using shared internal randomness but independent reward realizations, produce the same action sequence with probability at least $1-ρ$. Prior work is primarily elimination-based and, in linear bandits with infinitely many actions, relies on discretization, leading to suboptimal dependence on the dimension $d$ and $ρ$. We develop optimistic alternatives for both settings. For stochastic multi-armed bandits, we propose RepUCB, a replicable batched UCB algorithm and show that it attains a regret $O\!\left(\frac{K^2\log^2 T}{ρ^2}\sum_{a:Δ_a>0}\left(Δ_a+\frac{\log(KT\log T)}{Δ_a}\right)\right)$. For stochastic linear bandits, we first introduce RepRidge, a replicable ridge regression estimator that satisfies both a confidence guarantee and a $ρ$-replicability guarantee. Beyond its role in our bandit algorithm, this estimator and its guarantees may also be of independent interest in other statistical estimation settings. We then use RepRidge to design RepLinUCB, a replicable optimistic algorithm for stochastic linear bandits, and show that its regret is bounded by $\widetilde{O}\!\big(\big(d+\frac{d^3}ρ\big)\sqrt{T}\big)$. This improves the best prior regret guarantee by a factor of $O(d/ρ)$, showing that our optimistic algorithm can substantially reduce the price of replicability.

KMM-CP: Practical Conformal Prediction under Covariate Shift via Selective Kernel Mean Matching

Uncertainty quantification is essential for deploying machine learning models in high-stakes domains such as scientific discovery and healthcare. Conformal Prediction (CP) provides finite-sample coverage guarantees under exchangeability, an assumption often violated in practice due to distribution shift. Under covariate shift, restoring validity requires importance weighting, yet accurate density-ratio estimation becomes unstable when training and test distributions exhibit limited support overlap. We propose KMM-CP, a conformal prediction framework based on Kernel Mean Matching (KMM) for covariate-shift correction. We show that KMM directly controls the bias-variance components governing conformal coverage error by minimizing RKHS moment discrepancy under explicit weight constraints, and establish asymptotic coverage guarantees under mild conditions. We then introduce a selective extension that identifies regions of reliable support overlap and restricts conformal correction to this subset, further improving stability in low-overlap regimes. Experiments on molecular property prediction benchmarks with realistic distribution shifts show that KMM-CP reduces coverage gap by over 50% compared to existing approaches. The code is available at https://github.com/siddharthal/KMM-CP.

Model Predictive Control with Differentiable World Models for Offline Reinforcement Learning

Offline Reinforcement Learning (RL) aims to learn optimal policies from fixed offline datasets, without further interactions with the environment. Such methods train an offline policy (or value function), and apply it at inference time without further refinement. We introduce an inference time adaptation framework inspired by model predictive control (MPC) that utilizes a pretrained policy along with a learned world model of state transitions and rewards. While existing world model and diffusion-planning methods use learned dynamics to generate imagined trajectories during training, or to sample candidate plans at inference time, they do not use inference-time information to optimize the policy parameters on the fly. In contrast, our design is a Differentiable World Model (DWM) pipeline that enables endto-end gradient computation through imagined rollouts for policy optimization at inference time based on MPC. We evaluate our algorithm on D4RL continuous-control benchmarks (MuJoCo locomotion tasks and AntMaze), and show that exploiting inference-time information to optimize the policy parameters yields consistent gains over strong offline RL baselines.

FisherSFT: Data-Efficient Supervised Fine-Tuning of Language Models Using Information Gain

Supervised fine-tuning (SFT) is a standard approach to adapting large language models (LLMs) to new domains. In this work, we improve the statistical efficiency of SFT by selecting an informative subset of training examples. Specifically, for a fixed budget of training examples, which determines the computational cost of fine-tuning, we determine the most informative ones. The key idea in our method is to select examples that maximize information gain, measured by the Hessian of the log-likelihood of the LLM. We approximate it efficiently by linearizing the LLM at the last layer using multinomial logistic regression models. Our approach is computationally efficient, analyzable, and performs well empirically. We demonstrate this on several problems, and back our claims with both quantitative results and an LLM evaluation.

Conservative Contextual Bandits: Beyond Linear Representations

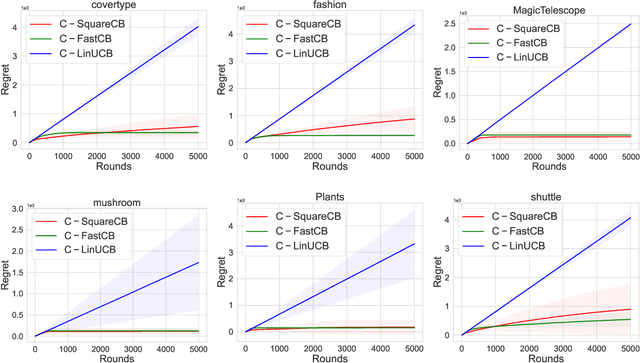
Conservative Contextual Bandits (CCBs) address safety in sequential decision making by requiring that an agent's policy, along with minimizing regret, also satisfies a safety constraint: the performance is not worse than a baseline policy (e.g., the policy that the company has in production) by more than $(1+\alpha)$ factor. Prior work developed UCB-style algorithms in the multi-armed [Wu et al., 2016] and contextual linear [Kazerouni et al., 2017] settings. However, in practice the cost of the arms is often a non-linear function, and therefore existing UCB algorithms are ineffective in such settings. In this paper, we consider CCBs beyond the linear case and develop two algorithms $\mathtt{C-SquareCB}$ and $\mathtt{C-FastCB}$, using Inverse Gap Weighting (IGW) based exploration and an online regression oracle. We show that the safety constraint is satisfied with high probability and that the regret of $\mathtt{C-SquareCB}$ is sub-linear in horizon $T$, while the regret of $\mathtt{C-FastCB}$ is first-order and is sub-linear in $L^*$, the cumulative loss of the optimal policy. Subsequently, we use a neural network for function approximation and online gradient descent as the regression oracle to provide $\tilde{O}(\sqrt{KT} + K/\alpha) $ and $\tilde{O}(\sqrt{KL^*} + K (1 + 1/\alpha))$ regret bounds, respectively. Finally, we demonstrate the efficacy of our algorithms on real-world data and show that they significantly outperform the existing baseline while maintaining the performance guarantee.

Think Before You Duel: Understanding Complexities of Preference Learning under Constrained Resources

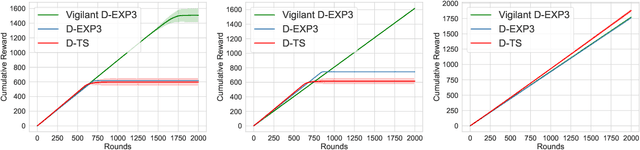
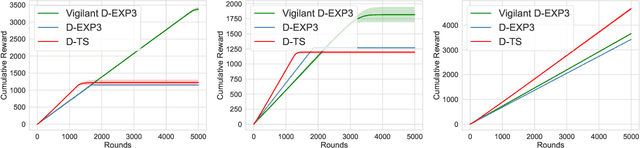
We consider the problem of reward maximization in the dueling bandit setup along with constraints on resource consumption. As in the classic dueling bandits, at each round the learner has to choose a pair of items from a set of $K$ items and observe a relative feedback for the current pair. Additionally, for both items, the learner also observes a vector of resource consumptions. The objective of the learner is to maximize the cumulative reward, while ensuring that the total consumption of any resource is within the allocated budget. We show that due to the relative nature of the feedback, the problem is more difficult than its bandit counterpart and that without further assumptions the problem is not learnable from a regret minimization perspective. Thereafter, by exploiting assumptions on the available budget, we provide an EXP3 based dueling algorithm that also considers the associated consumptions and show that it achieves an $\tilde{\mathcal{O}}\left({\frac{OPT^{(b)}}{B}}K^{1/3}T^{2/3}\right)$ regret, where $OPT^{(b)}$ is the optimal value and $B$ is the available budget. Finally, we provide numerical simulations to demonstrate the efficacy of our proposed method.

Contextual Bandits with Online Neural Regression

Recent works have shown a reduction from contextual bandits to online regression under a realizability assumption [Foster and Rakhlin, 2020, Foster and Krishnamurthy, 2021]. In this work, we investigate the use of neural networks for such online regression and associated Neural Contextual Bandits (NeuCBs). Using existing results for wide networks, one can readily show a ${\mathcal{O}}(\sqrt{T})$ regret for online regression with square loss, which via the reduction implies a ${\mathcal{O}}(\sqrt{K} T^{3/4})$ regret for NeuCBs. Departing from this standard approach, we first show a $\mathcal{O}(\log T)$ regret for online regression with almost convex losses that satisfy QG (Quadratic Growth) condition, a generalization of the PL (Polyak-\L ojasiewicz) condition, and that have a unique minima. Although not directly applicable to wide networks since they do not have unique minima, we show that adding a suitable small random perturbation to the network predictions surprisingly makes the loss satisfy QG with unique minima. Based on such a perturbed prediction, we show a ${\mathcal{O}}(\log T)$ regret for online regression with both squared loss and KL loss, and subsequently convert these respectively to $\tilde{\mathcal{O}}(\sqrt{KT})$ and $\tilde{\mathcal{O}}(\sqrt{KL^*} + K)$ regret for NeuCB, where $L^*$ is the loss of the best policy. Separately, we also show that existing regret bounds for NeuCBs are $\Omega(T)$ or assume i.i.d. contexts, unlike this work. Finally, our experimental results on various datasets demonstrate that our algorithms, especially the one based on KL loss, persistently outperform existing algorithms.

Schedule Based Temporal Difference Algorithms

Learning the value function of a given policy from data samples is an important problem in Reinforcement Learning. TD($\lambda$) is a popular class of algorithms to solve this problem. However, the weights assigned to different $n$-step returns in TD($\lambda$), controlled by the parameter $\lambda$, decrease exponentially with increasing $n$. In this paper, we present a $\lambda$-schedule procedure that generalizes the TD($\lambda$) algorithm to the case when the parameter $\lambda$ could vary with time-step. This allows flexibility in weight assignment, i.e., the user can specify the weights assigned to different $n$-step returns by choosing a sequence $\{\lambda_t\}_{t \geq 1}$. Based on this procedure, we propose an on-policy algorithm - TD($\lambda$)-schedule, and two off-policy algorithms - GTD($\lambda$)-schedule and TDC($\lambda$)-schedule, respectively. We provide proofs of almost sure convergence for all three algorithms under a general Markov noise framework.

Gradient Temporal Difference with Momentum: Stability and Convergence

Gradient temporal difference (Gradient TD) algorithms are a popular class of stochastic approximation (SA) algorithms used for policy evaluation in reinforcement learning. Here, we consider Gradient TD algorithms with an additional heavy ball momentum term and provide choice of step size and momentum parameter that ensures almost sure convergence of these algorithms asymptotically. In doing so, we decompose the heavy ball Gradient TD iterates into three separate iterates with different step sizes. We first analyze these iterates under one-timescale SA setting using results from current literature. However, the one-timescale case is restrictive and a more general analysis can be provided by looking at a three-timescale decomposition of the iterates. In the process, we provide the first conditions for stability and convergence of general three-timescale SA. We then prove that the heavy ball Gradient TD algorithm is convergent using our three-timescale SA analysis. Finally, we evaluate these algorithms on standard RL problems and report improvement in performance over the vanilla algorithms.

Does Momentum Help? A Sample Complexity Analysis

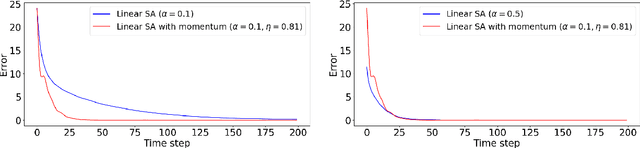
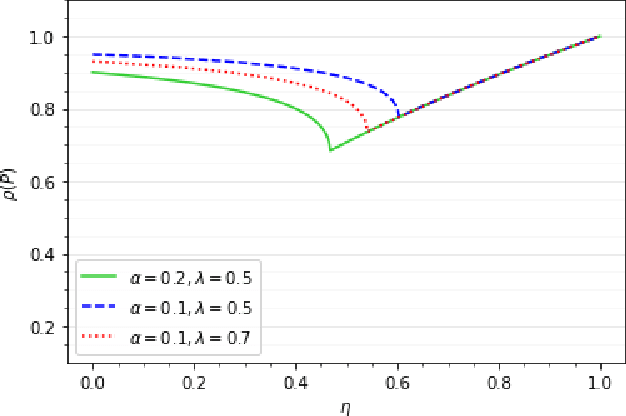
Momentum methods are popularly used in accelerating stochastic iterative methods. Although a fair amount of literature is dedicated to momentum in stochastic optimisation, there are limited results that quantify the benefits of using heavy ball momentum in the specific case of stochastic approximation algorithms. We first show that the convergence rate with optimal step size does not improve when momentum is used (under some assumptions). Secondly, to quantify the behaviour in the initial phase we analyse the sample complexity of iterates with and without momentum. We show that the sample complexity bound for SA without momentum is $\tilde{\mathcal{O}}(\frac{1}{\alpha\lambda_{min}(A)})$ while for SA with momentum is $\tilde{\mathcal{O}}(\frac{1}{\sqrt{\alpha\lambda_{min}(A)}})$, where $\alpha$ is the step size and $\lambda_{min}(A)$ is the smallest eigenvalue of the driving matrix $A$. Although the sample complexity bound for SA with momentum is better for small enough $\alpha$, it turns out that for optimal choice of $\alpha$ in the two cases, the sample complexity bounds are of the same order.