Does Momentum Help? A Sample Complexity Analysis
Paper and Code
Oct 29, 2021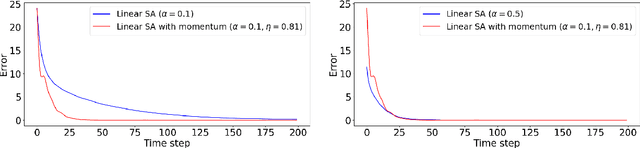
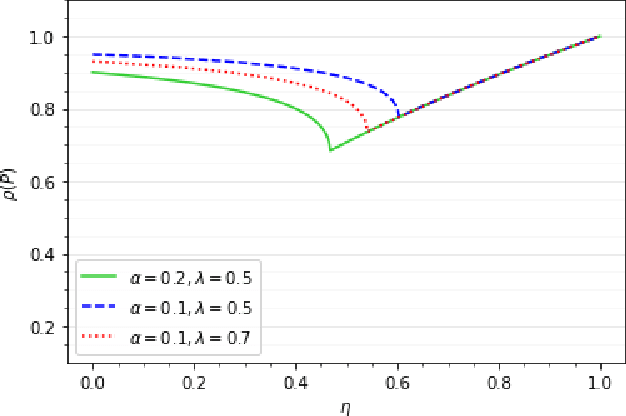
Momentum methods are popularly used in accelerating stochastic iterative methods. Although a fair amount of literature is dedicated to momentum in stochastic optimisation, there are limited results that quantify the benefits of using heavy ball momentum in the specific case of stochastic approximation algorithms. We first show that the convergence rate with optimal step size does not improve when momentum is used (under some assumptions). Secondly, to quantify the behaviour in the initial phase we analyse the sample complexity of iterates with and without momentum. We show that the sample complexity bound for SA without momentum is $\tilde{\mathcal{O}}(\frac{1}{\alpha\lambda_{min}(A)})$ while for SA with momentum is $\tilde{\mathcal{O}}(\frac{1}{\sqrt{\alpha\lambda_{min}(A)}})$, where $\alpha$ is the step size and $\lambda_{min}(A)$ is the smallest eigenvalue of the driving matrix $A$. Although the sample complexity bound for SA with momentum is better for small enough $\alpha$, it turns out that for optimal choice of $\alpha$ in the two cases, the sample complexity bounds are of the same order.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge