Efficient $Q$-Learning and Actor-Critic Methods for Robust Average Reward Reinforcement Learning

We present the first $Q$-learning and actor-critic algorithms for robust average reward Markov Decision Processes (MDPs) with non-asymptotic convergence under contamination, TV distance and Wasserstein distance uncertainty sets. We show that the robust $Q$ Bellman operator is a strict contractive mapping with respect to a carefully constructed semi-norm with constant functions being quotiented out. This property supports a stochastic approximation update, that learns the optimal robust $Q$ function in $\tilde{\cO}(\epsilon^{-2})$ samples. We also show that the same idea can be used for robust $Q$ function estimation, which can be further used for critic estimation. Coupling it with theories in robust policy mirror descent update, we present a natural actor-critic algorithm that attains an $\epsilon$-optimal robust policy in $\tilde{\cO}(\epsilon^{-3})$ samples. These results advance the theory of distributionally robust reinforcement learning in the average reward setting.

Regret Analysis of Average-Reward Unichain MDPs via an Actor-Critic Approach

Actor-Critic methods are widely used for their scalability, yet existing theoretical guarantees for infinite-horizon average-reward Markov Decision Processes (MDPs) often rely on restrictive ergodicity assumptions. We propose NAC-B, a Natural Actor-Critic with Batching, that achieves order-optimal regret of $\tilde{O}(\sqrt{T})$ in infinite-horizon average-reward MDPs under the unichain assumption, which permits both transient states and periodicity. This assumption is among the weakest under which the classic policy gradient theorem remains valid for average-reward settings. NAC-B employs function approximation for both the actor and the critic, enabling scalability to problems with large state and action spaces. The use of batching in our algorithm helps mitigate potential periodicity in the MDP and reduces stochasticity in gradient estimates, and our analysis formalizes these benefits through the introduction of the constants $C_{\text{hit}}$ and $C_{\text{tar}}$, which characterize the rate at which empirical averages over Markovian samples converge to the stationary distribution.

Global Convergence for Average Reward Constrained MDPs with Primal-Dual Actor Critic Algorithm

This paper investigates infinite-horizon average reward Constrained Markov Decision Processes (CMDPs) with general parametrization. We propose a Primal-Dual Natural Actor-Critic algorithm that adeptly manages constraints while ensuring a high convergence rate. In particular, our algorithm achieves global convergence and constraint violation rates of $\tilde{\mathcal{O}}(1/\sqrt{T})$ over a horizon of length $T$ when the mixing time, $\tau_{\mathrm{mix}}$, is known to the learner. In absence of knowledge of $\tau_{\mathrm{mix}}$, the achievable rates change to $\tilde{\mathcal{O}}(1/T^{0.5-\epsilon})$ provided that $T \geq \tilde{\mathcal{O}}\left(\tau_{\mathrm{mix}}^{2/\epsilon}\right)$. Our results match the theoretical lower bound for Markov Decision Processes and establish a new benchmark in the theoretical exploration of average reward CMDPs.

An Accelerated Multi-level Monte Carlo Approach for Average Reward Reinforcement Learning with General Policy Parametrization

In our study, we delve into average-reward reinforcement learning with general policy parametrization. Within this domain, current guarantees either fall short with suboptimal guarantees or demand prior knowledge of mixing time. To address these issues, we introduce Randomized Accelerated Natural Actor Critic, a method that integrates Multi-level Monte-Carlo and Natural Actor Critic. Our approach is the first to achieve global convergence rate of $\tilde{\mathcal{O}}(1/\sqrt{T})$ without requiring knowledge of mixing time, significantly surpassing the state-of-the-art bound of $\tilde{\mathcal{O}}(1/T^{1/4})$.

Variance-Reduced Policy Gradient Approaches for Infinite Horizon Average Reward Markov Decision Processes

We present two Policy Gradient-based methods with general parameterization in the context of infinite horizon average reward Markov Decision Processes. The first approach employs Implicit Gradient Transport for variance reduction, ensuring an expected regret of the order $\tilde{\mathcal{O}}(T^{3/5})$. The second approach, rooted in Hessian-based techniques, ensures an expected regret of the order $\tilde{\mathcal{O}}(\sqrt{T})$. These results significantly improve the state of the art of the problem, which achieves a regret of $\tilde{\mathcal{O}}(T^{3/4})$.

Global Convergence Guarantees for Federated Policy Gradient Methods with Adversaries

Federated Reinforcement Learning (FRL) allows multiple agents to collaboratively build a decision making policy without sharing raw trajectories. However, if a small fraction of these agents are adversarial, it can lead to catastrophic results. We propose a policy gradient based approach that is robust to adversarial agents which can send arbitrary values to the server. Under this setting, our results form the first global convergence guarantees with general parametrization. These results demonstrate resilience with adversaries, while achieving sample complexity of order $\tilde{\mathcal{O}}\left( \frac{1}{\epsilon^2} \left( \frac{1}{N-f} + \frac{f^2}{(N-f)^2}\right)\right)$, where $N$ is the total number of agents and $f$ is the number of adversarial agents.

Online Learning with Adversaries: A Differential Inclusion Analysis

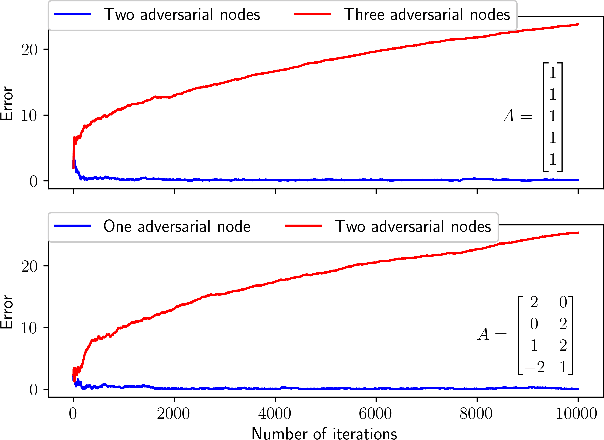
We consider the measurement model $Y = AX,$ where $X$ and, hence, $Y$ are random variables and $A$ is an a priori known tall matrix. At each time instance, a sample of one of $Y$'s coordinates is available, and the goal is to estimate $\mu := \mathbb{E}[X]$ via these samples. However, the challenge is that a small but unknown subset of $Y$'s coordinates are controlled by adversaries with infinite power: they can return any real number each time they are queried for a sample. For such an adversarial setting, we propose the first asynchronous online algorithm that converges to $\mu$ almost surely. We prove this result using a novel differential inclusion based two-timescale analysis. Two key highlights of our proof include: (a) the use of a novel Lyapunov function for showing that $\mu$ is the unique global attractor for our algorithm's limiting dynamics, and (b) the use of martingale and stopping time theory to show that our algorithm's iterates are almost surely bounded.

Does Momentum Help? A Sample Complexity Analysis

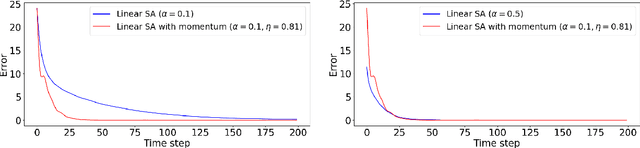
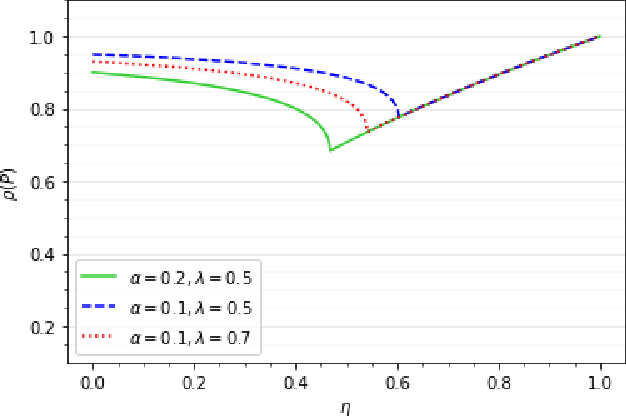
Momentum methods are popularly used in accelerating stochastic iterative methods. Although a fair amount of literature is dedicated to momentum in stochastic optimisation, there are limited results that quantify the benefits of using heavy ball momentum in the specific case of stochastic approximation algorithms. We first show that the convergence rate with optimal step size does not improve when momentum is used (under some assumptions). Secondly, to quantify the behaviour in the initial phase we analyse the sample complexity of iterates with and without momentum. We show that the sample complexity bound for SA without momentum is $\tilde{\mathcal{O}}(\frac{1}{\alpha\lambda_{min}(A)})$ while for SA with momentum is $\tilde{\mathcal{O}}(\frac{1}{\sqrt{\alpha\lambda_{min}(A)}})$, where $\alpha$ is the step size and $\lambda_{min}(A)$ is the smallest eigenvalue of the driving matrix $A$. Although the sample complexity bound for SA with momentum is better for small enough $\alpha$, it turns out that for optimal choice of $\alpha$ in the two cases, the sample complexity bounds are of the same order.