Last-Iterate Convergence of General Parameterized Policies in Constrained MDPs

We consider the problem of learning a Constrained Markov Decision Process (CMDP) via general parameterization. Our proposed Primal-Dual based Regularized Accelerated Natural Policy Gradient (PDR-ANPG) algorithm uses entropy and quadratic regularizers to reach this goal. For a parameterized policy class with transferred compatibility approximation error, $\epsilon_{\mathrm{bias}}$, PDR-ANPG achieves a last-iterate $\epsilon$ optimality gap and $\epsilon$ constraint violation (up to some additive factor of $\epsilon_{\mathrm{bias}}$) with a sample complexity of $\tilde{\mathcal{O}}(\epsilon^{-2}\min\{\epsilon^{-2},\epsilon_{\mathrm{bias}}^{-\frac{1}{3}}\})$. If the class is incomplete ($\epsilon_{\mathrm{bias}}>0$), then the sample complexity reduces to $\tilde{\mathcal{O}}(\epsilon^{-2})$ for $\epsilon<(\epsilon_{\mathrm{bias}})^{\frac{1}{6}}$. Moreover, for complete policies with $\epsilon_{\mathrm{bias}}=0$, our algorithm achieves a last-iterate $\epsilon$ optimality gap and $\epsilon$ constraint violation with $\tilde{\mathcal{O}}(\epsilon^{-4})$ sample complexity. It is a significant improvement of the state-of-the-art last-iterate guarantees of general parameterized CMDPs.

Sample-Efficient Constrained Reinforcement Learning with General Parameterization

We consider a constrained Markov Decision Problem (CMDP) where the goal of an agent is to maximize the expected discounted sum of rewards over an infinite horizon while ensuring that the expected discounted sum of costs exceeds a certain threshold. Building on the idea of momentum-based acceleration, we develop the Primal-Dual Accelerated Natural Policy Gradient (PD-ANPG) algorithm that guarantees an $\epsilon$ global optimality gap and $\epsilon$ constraint violation with $\mathcal{O}(\epsilon^{-3})$ sample complexity. This improves the state-of-the-art sample complexity in CMDP by a factor of $\mathcal{O}(\epsilon^{-1})$.

Variance-Reduced Policy Gradient Approaches for Infinite Horizon Average Reward Markov Decision Processes

We present two Policy Gradient-based methods with general parameterization in the context of infinite horizon average reward Markov Decision Processes. The first approach employs Implicit Gradient Transport for variance reduction, ensuring an expected regret of the order $\tilde{\mathcal{O}}(T^{3/5})$. The second approach, rooted in Hessian-based techniques, ensures an expected regret of the order $\tilde{\mathcal{O}}(\sqrt{T})$. These results significantly improve the state of the art of the problem, which achieves a regret of $\tilde{\mathcal{O}}(T^{3/4})$.

Learning General Parameterized Policies for Infinite Horizon Average Reward Constrained MDPs via Primal-Dual Policy Gradient Algorithm

This paper explores the realm of infinite horizon average reward Constrained Markov Decision Processes (CMDP). To the best of our knowledge, this work is the first to delve into the regret and constraint violation analysis of average reward CMDPs with a general policy parametrization. To address this challenge, we propose a primal dual based policy gradient algorithm that adeptly manages the constraints while ensuring a low regret guarantee toward achieving a global optimal policy. In particular, we demonstrate that our proposed algorithm achieves $\tilde{\mathcal{O}}({T}^{3/4})$ objective regret and $\tilde{\mathcal{O}}({T}^{3/4})$ constraint violation bounds.

Improved Sample Complexity Analysis of Natural Policy Gradient Algorithm with General Parameterization for Infinite Horizon Discounted Reward Markov Decision Processes

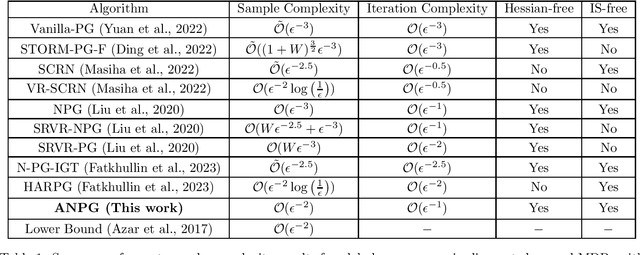
We consider the problem of designing sample efficient learning algorithms for infinite horizon discounted reward Markov Decision Process. Specifically, we propose the Accelerated Natural Policy Gradient (ANPG) algorithm that utilizes an accelerated stochastic gradient descent process to obtain the natural policy gradient. ANPG achieves $\mathcal{O}({\epsilon^{-2}})$ sample complexity and $\mathcal{O}(\epsilon^{-1})$ iteration complexity with general parameterization where $\epsilon$ defines the optimality error. This improves the state-of-the-art sample complexity by a $\log(\frac{1}{\epsilon})$ factor. ANPG is a first-order algorithm and unlike some existing literature, does not require the unverifiable assumption that the variance of importance sampling (IS) weights is upper bounded. In the class of Hessian-free and IS-free algorithms, ANPG beats the best-known sample complexity by a factor of $\mathcal{O}(\epsilon^{-\frac{1}{2}})$ and simultaneously matches their state-of-the-art iteration complexity.

Regret Analysis of Policy Gradient Algorithm for Infinite Horizon Average Reward Markov Decision Processes

In this paper, we consider an infinite horizon average reward Markov Decision Process (MDP). Distinguishing itself from existing works within this context, our approach harnesses the power of the general policy gradient-based algorithm, liberating it from the constraints of assuming a linear MDP structure. We propose a policy gradient-based algorithm and show its global convergence property. We then prove that the proposed algorithm has $\tilde{\mathcal{O}}({T}^{3/4})$ regret. Remarkably, this paper marks a pioneering effort by presenting the first exploration into regret-bound computation for the general parameterized policy gradient algorithm in the context of average reward scenarios.

Cooperating Graph Neural Networks with Deep Reinforcement Learning for Vaccine Prioritization

This study explores the vaccine prioritization strategy to reduce the overall burden of the pandemic when the supply is limited. Existing methods conduct macro-level or simplified micro-level vaccine distribution by assuming the homogeneous behavior within subgroup populations and lacking mobility dynamics integration. Directly applying these models for micro-level vaccine allocation leads to sub-optimal solutions due to the lack of behavioral-related details. To address the issue, we first incorporate the mobility heterogeneity in disease dynamics modeling and mimic the disease evolution process using a Trans-vaccine-SEIR model. Then we develop a novel deep reinforcement learning to seek the optimal vaccine allocation strategy for the high-degree spatial-temporal disease evolution system. The graph neural network is used to effectively capture the structural properties of the mobility contact network and extract the dynamic disease features. In our evaluation, the proposed framework reduces 7% - 10% of infections and deaths than the baseline strategies. Extensive evaluation shows that the proposed framework is robust to seek the optimal vaccine allocation with diverse mobility patterns in the micro-level disease evolution system. In particular, we find the optimal vaccine allocation strategy in the transit usage restriction scenario is significantly more effective than restricting cross-zone mobility for the top 10% age-based and income-based zones. These results provide valuable insights for areas with limited vaccines and low logistic efficacy.

Reinforcement Learning with Delayed, Composite, and Partially Anonymous Reward

We investigate an infinite-horizon average reward Markov Decision Process (MDP) with delayed, composite, and partially anonymous reward feedback. The delay and compositeness of rewards mean that rewards generated as a result of taking an action at a given state are fragmented into different components, and they are sequentially realized at delayed time instances. The partial anonymity attribute implies that a learner, for each state, only observes the aggregate of past reward components generated as a result of different actions taken at that state, but realized at the observation instance. We propose an algorithm named $\mathrm{DUCRL2}$ to obtain a near-optimal policy for this setting and show that it achieves a regret bound of $\tilde{\mathcal{O}}\left(DS\sqrt{AT} + d (SA)^3\right)$ where $S$ and $A$ are the sizes of the state and action spaces, respectively, $D$ is the diameter of the MDP, $d$ is a parameter upper bounded by the maximum reward delay, and $T$ denotes the time horizon. This demonstrates the optimality of the bound in the order of $T$, and an additive impact of the delay.

Mean-Field Control based Approximation of Multi-Agent Reinforcement Learning in Presence of a Non-decomposable Shared Global State

Mean Field Control (MFC) is a powerful approximation tool to solve large-scale Multi-Agent Reinforcement Learning (MARL) problems. However, the success of MFC relies on the presumption that given the local states and actions of all the agents, the next (local) states of the agents evolve conditionally independent of each other. Here we demonstrate that even in a MARL setting where agents share a common global state in addition to their local states evolving conditionally independently (thus introducing a correlation between the state transition processes of individual agents), the MFC can still be applied as a good approximation tool. The global state is assumed to be non-decomposable i.e., it cannot be expressed as a collection of local states of the agents. We compute the approximation error as $\mathcal{O}(e)$ where $e=\frac{1}{\sqrt{N}}\left[\sqrt{|\mathcal{X}|} +\sqrt{|\mathcal{U}|}\right]$. The size of the agent population is denoted by the term $N$, and $|\mathcal{X}|, |\mathcal{U}|$ respectively indicate the sizes of (local) state and action spaces of individual agents. The approximation error is found to be independent of the size of the shared global state space. We further demonstrate that in a special case if the reward and state transition functions are independent of the action distribution of the population, then the error can be improved to $e=\frac{\sqrt{|\mathcal{X}|}}{\sqrt{N}}$. Finally, we devise a Natural Policy Gradient based algorithm that solves the MFC problem with $\mathcal{O}(\epsilon^{-3})$ sample complexity and obtains a policy that is within $\mathcal{O}(\max\{e,\epsilon\})$ error of the optimal MARL policy for any $\epsilon>0$.

Mean-Field Approximation of Cooperative Constrained Multi-Agent Reinforcement Learning (CMARL)

Mean-Field Control (MFC) has recently been proven to be a scalable tool to approximately solve large-scale multi-agent reinforcement learning (MARL) problems. However, these studies are typically limited to unconstrained cumulative reward maximization framework. In this paper, we show that one can use the MFC approach to approximate the MARL problem even in the presence of constraints. Specifically, we prove that, an $N$-agent constrained MARL problem, with state, and action spaces of each individual agents being of sizes $|\mathcal{X}|$, and $|\mathcal{U}|$ respectively, can be approximated by an associated constrained MFC problem with an error, $e\triangleq \mathcal{O}\left([\sqrt{|\mathcal{X}|}+\sqrt{|\mathcal{U}|}]/\sqrt{N}\right)$. In a special case where the reward, cost, and state transition functions are independent of the action distribution of the population, we prove that the error can be improved to $e=\mathcal{O}(\sqrt{|\mathcal{X}|}/\sqrt{N})$. Also, we provide a Natural Policy Gradient based algorithm and prove that it can solve the constrained MARL problem within an error of $\mathcal{O}(e)$ with a sample complexity of $\mathcal{O}(e^{-6})$.