Stabilizing Fixed-Point Iteration for Markov Chain Poisson Equations

Poisson equations underpin average-reward reinforcement learning, but beyond ergodicity they can be ill-posed, meaning that solutions are non-unique and standard fixed point iterations can oscillate on reducible or periodic chains. We study finite-state Markov chains with $n$ states and transition matrix $P$. We show that all non-decaying modes are captured by a real peripheral invariant subspace $\mathcal{K}(P)$, and that the induced operator on the quotient space $\mathbb{R}^n/\mathcal{K}(P)$ is strictly contractive, yielding a unique quotient solution. Building on this viewpoint, we develop an end-to-end pipeline that learns the chain structure, estimates an anchor based gauge map, and runs projected stochastic approximation to estimate a gauge-fixed representative together with an associated peripheral residual. We prove $\widetilde{O}(T^{-1/2})$ convergence up to projection estimation error, enabling stable Poisson equation learning for multichain and periodic regimes with applications to performance evaluation of average-reward reinforcement learning beyond ergodicity.

Sample Complexity Analysis for Constrained Bilevel Reinforcement Learning

Several important problem settings within the literature of reinforcement learning (RL), such as meta-learning, hierarchical learning, and RL from human feedback (RL-HF), can be modelled as bilevel RL problems. A lot has been achieved in these domains empirically; however, the theoretical analysis of bilevel RL algorithms hasn't received a lot of attention. In this work, we analyse the sample complexity of a constrained bilevel RL algorithm, building on the progress in the unconstrained setting. We obtain an iteration complexity of $O(ε^{-2})$ and sample complexity of $\tilde{O}(ε^{-4})$ for our proposed algorithm, Constrained Bilevel Subgradient Optimization (CBSO). We use a penalty-based objective function to avoid the issue of primal-dual gap and hyper-gradient in the context of a constrained bilevel problem setting. The penalty-based formulation to handle constraints requires analysis of non-smooth optimization. We are the first ones to analyse the generally parameterized policy gradient-based RL algorithm with a non-smooth objective function using the Moreau envelope.

Order-Optimal Sample Complexity of Rectified Flows

Recently, flow-based generative models have shown superior efficiency compared to diffusion models. In this paper, we study rectified flow models, which constrain transport trajectories to be linear from the base distribution to the data distribution. This structural restriction greatly accelerates sampling, often enabling high-quality generation with a single Euler step. Under standard assumptions on the neural network classes used to parameterize the velocity field and data distribution, we prove that rectified flows achieve sample complexity $\tilde{O}(\varepsilon^{-2})$. This improves on the best known $O(\varepsilon^{-4})$ bounds for flow matching model and matches the optimal rate for mean estimation. Our analysis exploits the particular structure of rectified flows: because the model is trained with a squared loss along linear paths, the associated hypothesis class admits a sharply controlled localized Rademacher complexity. This yields the improved, order-optimal sample complexity and provides a theoretical explanation for the strong empirical performance of rectified flow models.

Stronger Approximation Guarantees for Non-Monotone γ-Weakly DR-Submodular Maximization

Maximizing submodular objectives under constraints is a fundamental problem in machine learning and optimization. We study the maximization of a nonnegative, non-monotone $γ$-weakly DR-submodular function over a down-closed convex body. Our main result is an approximation algorithm whose guarantee depends smoothly on $γ$; in particular, when $γ=1$ (the DR-submodular case) our bound recovers the $0.401$ approximation factor, while for $γ<1$ the guarantee degrades gracefully and, it improves upon previously reported bounds for $γ$-weakly DR-submodular maximization under the same constraints. Our approach combines a Frank-Wolfe-guided continuous-greedy framework with a $γ$-aware double-greedy step, yielding a simple yet effective procedure for handling non-monotonicity. This results in state-of-the-art guarantees for non-monotone $γ$-weakly DR-submodular maximization over down-closed convex bodies.

Distributionally Robust Self Paced Curriculum Reinforcement Learning

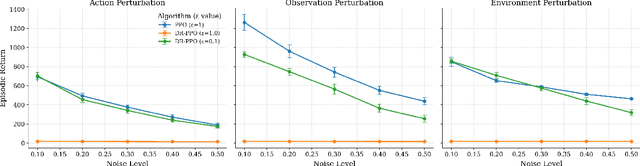
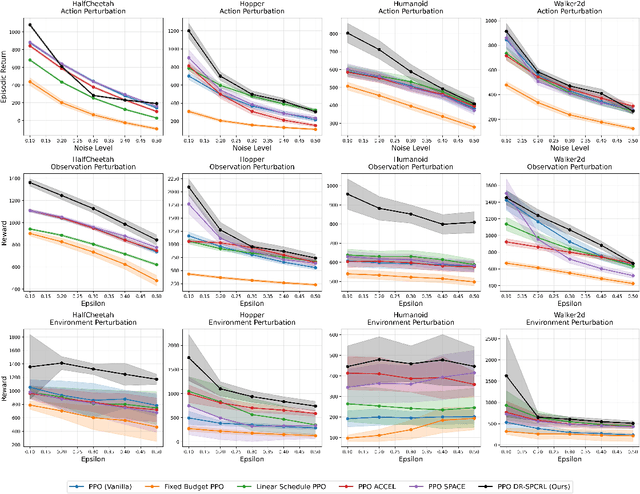
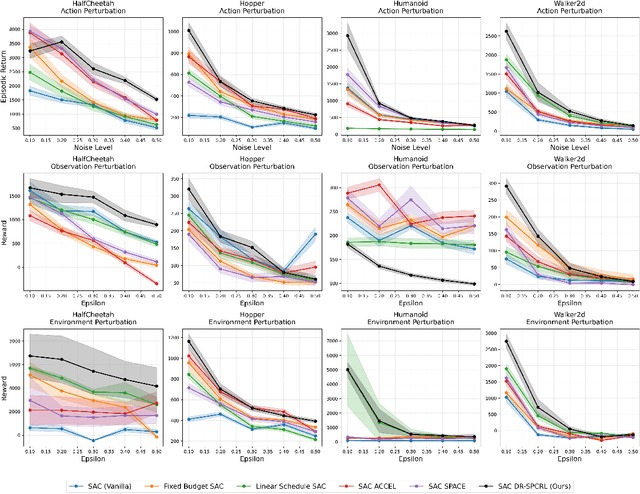
A central challenge in reinforcement learning is that policies trained in controlled environments often fail under distribution shifts at deployment into real-world environments. Distributionally Robust Reinforcement Learning (DRRL) addresses this by optimizing for worst-case performance within an uncertainty set defined by a robustness budget $ε$. However, fixing $ε$ results in a tradeoff between performance and robustness: small values yield high nominal performance but weak robustness, while large values can result in instability and overly conservative policies. We propose Distributionally Robust Self-Paced Curriculum Reinforcement Learning (DR-SPCRL), a method that overcomes this limitation by treating $ε$ as a continuous curriculum. DR-SPCRL adaptively schedules the robustness budget according to the agent's progress, enabling a balance between nominal and robust performance. Empirical results across multiple environments demonstrate that DR-SPCRL not only stabilizes training but also achieves a superior robustness-performance trade-off, yielding an average 11.8\% increase in episodic return under varying perturbations compared to fixed or heuristic scheduling strategies, and achieving approximately 1.9$\times$ the performance of the corresponding nominal RL algorithms.

Primal-Only Actor Critic Algorithm for Robust Constrained Average Cost MDPs

In this work, we study the problem of finding robust and safe policies in Robust Constrained Average-Cost Markov Decision Processes (RCMDPs). A key challenge in this setting is the lack of strong duality, which prevents the direct use of standard primal-dual methods for constrained RL. Additional difficulties arise from the average-cost setting, where the Robust Bellman operator is not a contraction under any norm. To address these challenges, we propose an actor-critic algorithm for Average-Cost RCMDPs. We show that our method achieves both \(ε\)-feasibility and \(ε\)-optimality, and we establish a sample complexities of \(\tilde{O}\left(ε^{-4}\right)\) and \(\tilde{O}\left(ε^{-6}\right)\) with and without slackness assumption, which is comparable to the discounted setting.

Contrastive Cross-Modal Learning for Infusing Chest X-ray Knowledge into ECGs

Modern diagnostic workflows are increasingly multimodal, integrating diverse data sources such as medical images, structured records, and physiological time series. Among these, electrocardiograms (ECGs) and chest X-rays (CXRs) are two of the most widely used modalities for cardiac assessment. While CXRs provide rich diagnostic information, ECGs are more accessible and can support scalable early warning systems. In this work, we propose CroMoTEX, a novel contrastive learning-based framework that leverages chest X-rays during training to learn clinically informative ECG representations for multiple cardiac-related pathologies: cardiomegaly, pleural effusion, and edema. Our method aligns ECG and CXR representations using a novel supervised cross-modal contrastive objective with adaptive hard negative weighting, enabling robust and task-relevant feature learning. At test time, CroMoTEX relies solely on ECG input, allowing scalable deployment in real-world settings where CXRs may be unavailable. Evaluated on the large-scale MIMIC-IV-ECG and MIMIC-CXR datasets, CroMoTEX outperforms baselines across all three pathologies, achieving up to 78.31 AUROC on edema. Our code is available at github.com/vineetpmoorty/cromotex.

Efficient $Q$-Learning and Actor-Critic Methods for Robust Average Reward Reinforcement Learning

We present the first $Q$-learning and actor-critic algorithms for robust average reward Markov Decision Processes (MDPs) with non-asymptotic convergence under contamination, TV distance and Wasserstein distance uncertainty sets. We show that the robust $Q$ Bellman operator is a strict contractive mapping with respect to a carefully constructed semi-norm with constant functions being quotiented out. This property supports a stochastic approximation update, that learns the optimal robust $Q$ function in $\tilde{\cO}(\epsilon^{-2})$ samples. We also show that the same idea can be used for robust $Q$ function estimation, which can be further used for critic estimation. Coupling it with theories in robust policy mirror descent update, we present a natural actor-critic algorithm that attains an $\epsilon$-optimal robust policy in $\tilde{\cO}(\epsilon^{-3})$ samples. These results advance the theory of distributionally robust reinforcement learning in the average reward setting.

Regret Analysis of Average-Reward Unichain MDPs via an Actor-Critic Approach

Actor-Critic methods are widely used for their scalability, yet existing theoretical guarantees for infinite-horizon average-reward Markov Decision Processes (MDPs) often rely on restrictive ergodicity assumptions. We propose NAC-B, a Natural Actor-Critic with Batching, that achieves order-optimal regret of $\tilde{O}(\sqrt{T})$ in infinite-horizon average-reward MDPs under the unichain assumption, which permits both transient states and periodicity. This assumption is among the weakest under which the classic policy gradient theorem remains valid for average-reward settings. NAC-B employs function approximation for both the actor and the critic, enabling scalability to problems with large state and action spaces. The use of batching in our algorithm helps mitigate potential periodicity in the MDP and reduces stochasticity in gradient estimates, and our analysis formalizes these benefits through the introduction of the constants $C_{\text{hit}}$ and $C_{\text{tar}}$, which characterize the rate at which empirical averages over Markovian samples converge to the stationary distribution.

Sample Complexity of Diffusion Model Training Without Empirical Risk Minimizer Access

Diffusion models have demonstrated state-of-the-art performance across vision, language, and scientific domains. Despite their empirical success, prior theoretical analyses of the sample complexity suffer from poor scaling with input data dimension or rely on unrealistic assumptions such as access to exact empirical risk minimizers. In this work, we provide a principled analysis of score estimation, establishing a sample complexity bound of $\widetilde{\mathcal{O}}(\epsilon^{-6})$. Our approach leverages a structured decomposition of the score estimation error into statistical, approximation, and optimization errors, enabling us to eliminate the exponential dependence on neural network parameters that arises in prior analyses. It is the first such result which achieves sample complexity bounds without assuming access to the empirical risk minimizer of score function estimation loss.