Rack Position Optimization in Large-Scale Heterogeneous Data Centers

As rapidly growing AI computational demands accelerate the need for new hardware installation and maintenance, this work explores optimal data center resource management by balancing operational efficiency with fault tolerance through strategic rack positioning considering diverse resources and locations. Traditional mixed-integer programming (MIP) approaches often struggle with scalability, while heuristic methods may result in significant sub-optimality. To address these issues, this paper presents a novel two-tier optimization framework using a high-level deep reinforcement learning (DRL) model to guide a low-level gradient-based heuristic for local search. The high-level DRL agent employs Leader Reward for optimal rack type ordering, and the low-level heuristic efficiently maps racks to positions, minimizing movement counts and ensuring fault-tolerant resource distribution. This approach allows scalability to over 100,000 positions and 100 rack types. Our method outperformed the gradient-based heuristic by 7\% on average and the MIP solver by over 30\% in objective value. It achieved a 100\% success rate versus MIP's 97.5\% (within a 20-minute limit), completing in just 2 minutes compared to MIP's 1630 minutes (i.e., almost 4 orders of magnitude improvement). Unlike the MIP solver, which showed performance variability under time constraints and high penalties, our algorithm consistently delivered stable, efficient results - an essential feature for large-scale data center management.

A Scale Invariant Approach for Sparse Signal Recovery

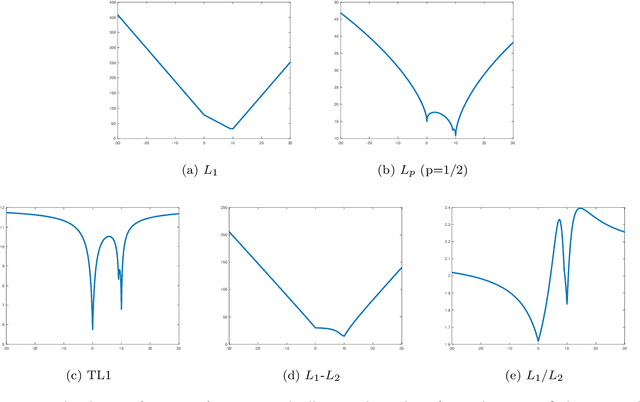
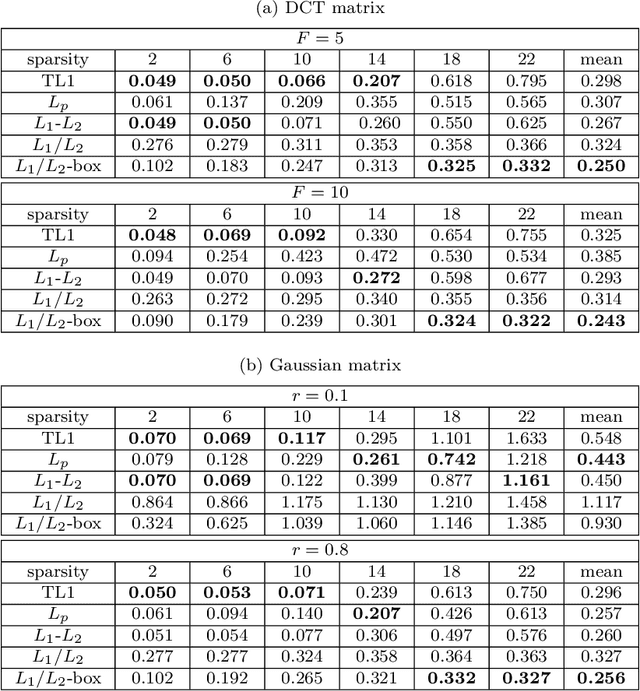
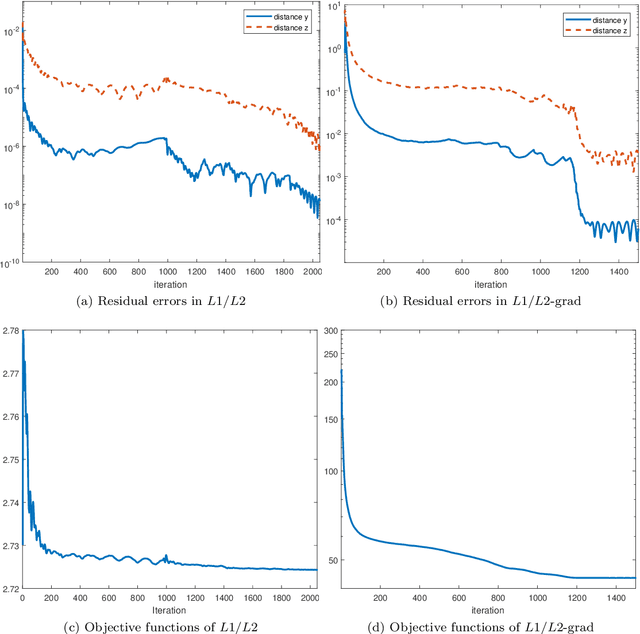
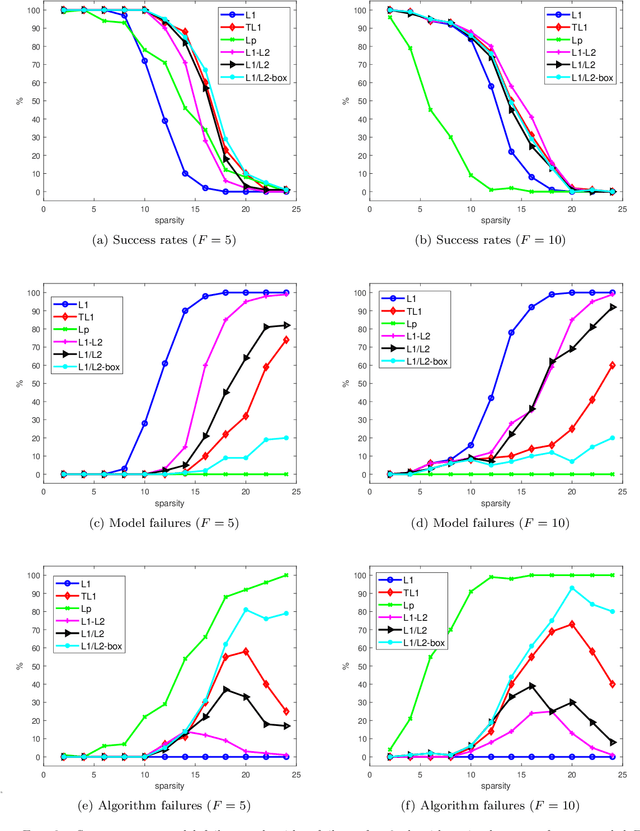
In this paper, we study the ratio of the $L_1 $ and $L_2 $ norms, denoted as $L_1/L_2$, to promote sparsity. Due to the non-convexity and non-linearity, there has been little attention to this scale-invariant metric. Compared to popular models in the literature such as the $L_p$ model for $p\in(0,1)$ and the transformed $L_1$ (TL1), this ratio model is parameter free. Theoretically, we present a weak null space property (wNSP) and prove that any sparse vector is a local minimizer of the $L_1 /L_2 $ model provided with this wNSP condition. Computationally, we focus on a constrained formulation that can be solved via the alternating direction method of multipliers (ADMM). Experiments show that the proposed approach is comparable to the state-of-the-art methods in sparse recovery. In addition, a variant of the $L_1/L_2$ model to apply on the gradient is also discussed with a proof-of-concept example of MRI reconstruction.construction.

On the exact recovery of sparse signals via conic relaxations

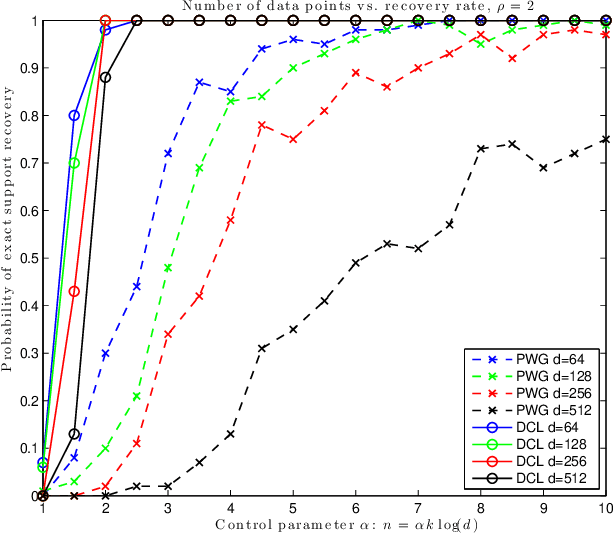
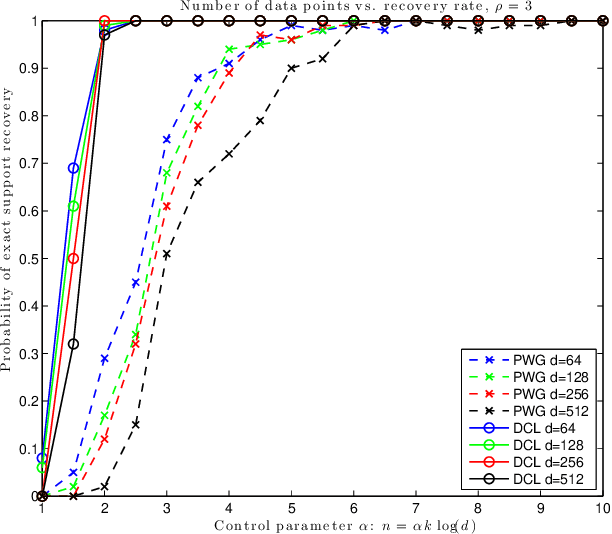
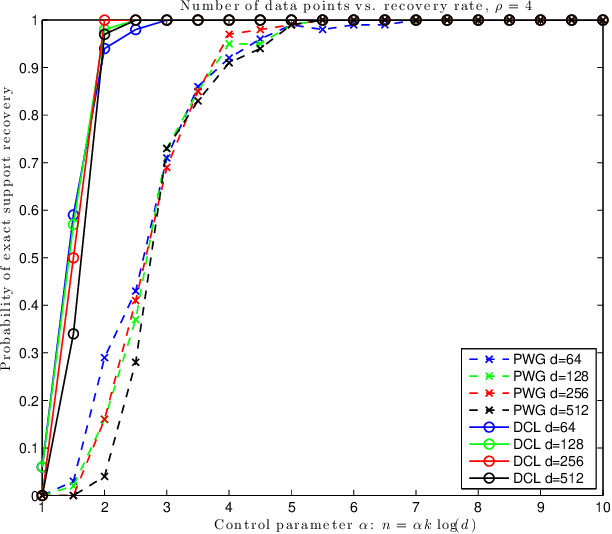
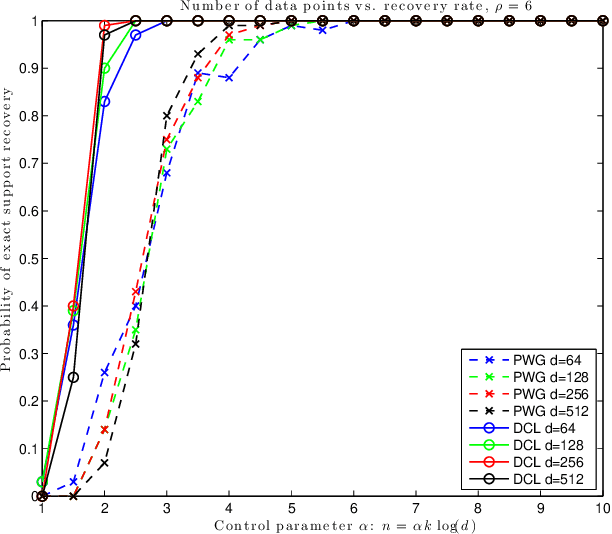
In this note we compare two recently proposed semidefinite relaxations for the sparse linear regression problem by Pilanci, Wainwright and El Ghaoui (Sparse learning via boolean relaxations, 2015) and Dong, Chen and Linderoth (Relaxation vs. Regularization A conic optimization perspective of statistical variable selection, 2015). We focus on the cardinality constrained formulation, and prove that the relaxation proposed by Dong, etc. is theoretically no weaker than the one proposed by Pilanci, etc. Therefore any sufficient condition of exact recovery derived by Pilanci can be readily applied to the other relaxation, including their results on high probability recovery for Gaussian ensemble. Finally we provide empirical evidence that the relaxation by Dong, etc. requires much fewer observations to guarantee the recovery of true support.

Regularization vs. Relaxation: A conic optimization perspective of statistical variable selection

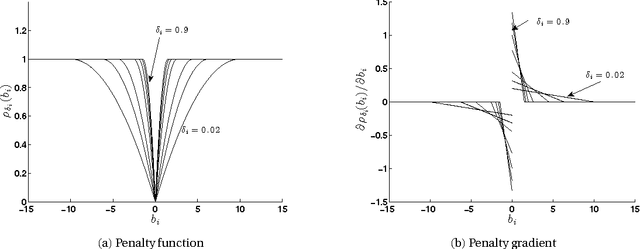
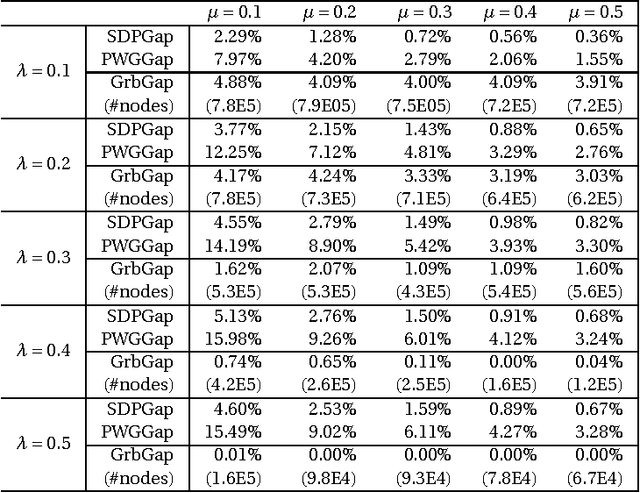
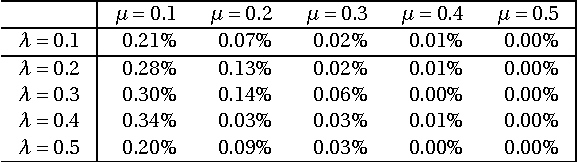
Variable selection is a fundamental task in statistical data analysis. Sparsity-inducing regularization methods are a popular class of methods that simultaneously perform variable selection and model estimation. The central problem is a quadratic optimization problem with an l0-norm penalty. Exactly enforcing the l0-norm penalty is computationally intractable for larger scale problems, so dif- ferent sparsity-inducing penalty functions that approximate the l0-norm have been introduced. In this paper, we show that viewing the problem from a convex relaxation perspective offers new insights. In particular, we show that a popular sparsity-inducing concave penalty function known as the Minimax Concave Penalty (MCP), and the reverse Huber penalty derived in a recent work by Pilanci, Wainwright and Ghaoui, can both be derived as special cases of a lifted convex relaxation called the perspective relaxation. The optimal perspective relaxation is a related minimax problem that balances the overall convexity and tightness of approximation to the l0 norm. We show it can be solved by a semidefinite relaxation. Moreover, a probabilistic interpretation of the semidefinite relaxation reveals connections with the boolean quadric polytope in combinatorial optimization. Finally by reformulating the l0-norm pe- nalized problem as a two-level problem, with the inner level being a Max-Cut problem, our proposed semidefinite relaxation can be realized by replacing the inner level problem with its semidefinite relaxation studied by Goemans and Williamson. This interpretation suggests using the Goemans-Williamson rounding procedure to find approximate solutions to the l0-norm penalized problem. Numerical experiments demonstrate the tightness of our proposed semidefinite relaxation, and the effectiveness of finding approximate solutions by Goemans-Williamson rounding.