Yaghoub Rahimi
A Lifted $\ell_1 $ Framework for Sparse Recovery
Mar 10, 2022



Abstract:Motivated by re-weighted $\ell_1$ approaches for sparse recovery, we propose a lifted $\ell_1$ (LL1) regularization which is a generalized form of several popular regularizations in the literature. By exploring such connections, we discover there are two types of lifting functions which can guarantee that the proposed approach is equivalent to the $\ell_0$ minimization. Computationally, we design an efficient algorithm via the alternating direction method of multiplier (ADMM) and establish the convergence for an unconstrained formulation. Experimental results are presented to demonstrate how this generalization improves sparse recovery over the state-of-the-art.
A Scale Invariant Approach for Sparse Signal Recovery
Jan 05, 2019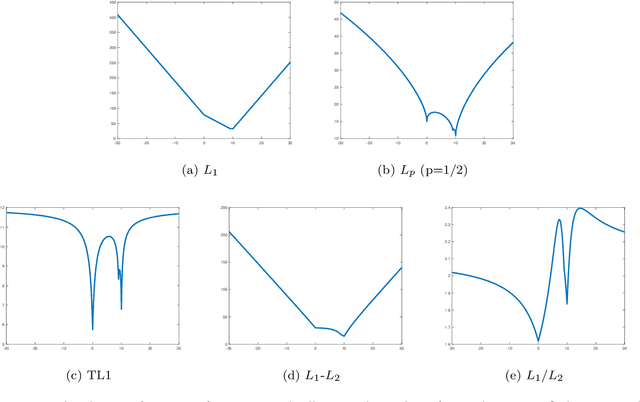
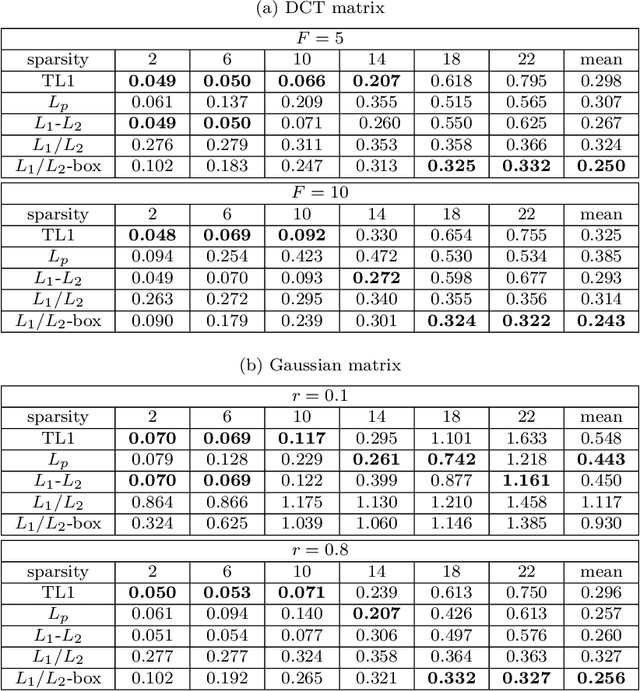
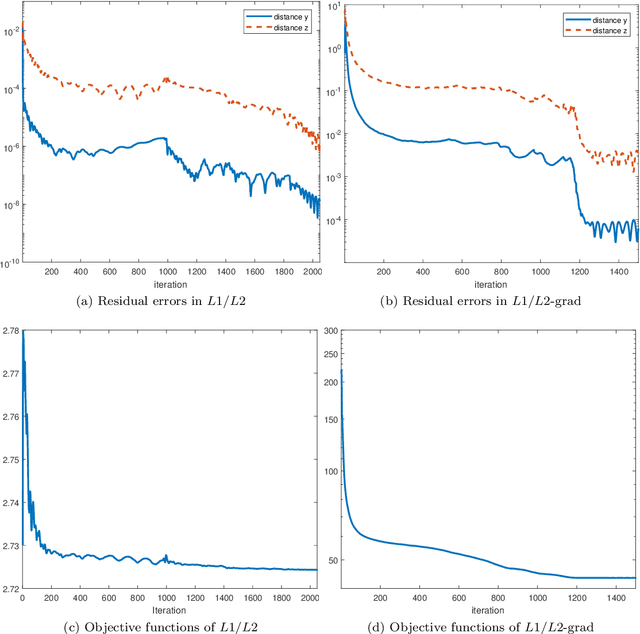
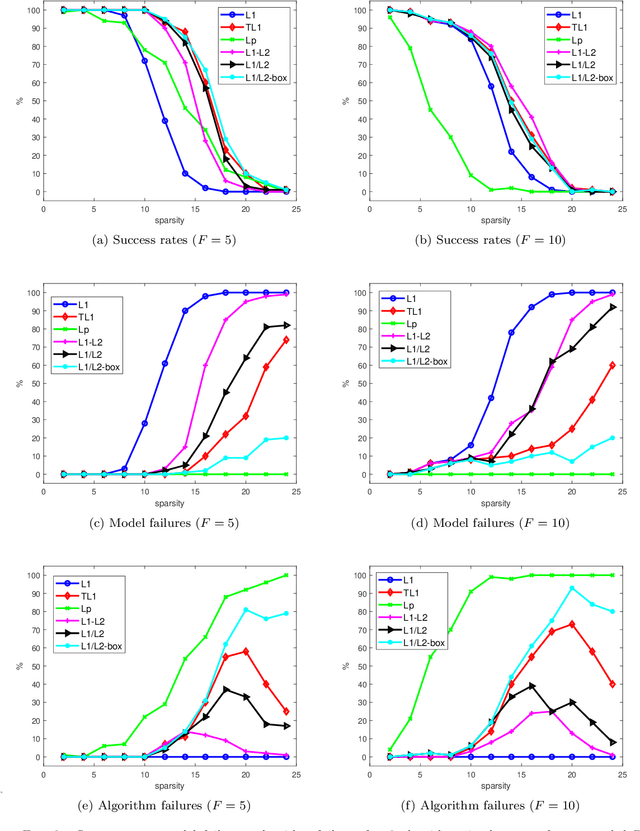
Abstract:In this paper, we study the ratio of the $L_1 $ and $L_2 $ norms, denoted as $L_1/L_2$, to promote sparsity. Due to the non-convexity and non-linearity, there has been little attention to this scale-invariant metric. Compared to popular models in the literature such as the $L_p$ model for $p\in(0,1)$ and the transformed $L_1$ (TL1), this ratio model is parameter free. Theoretically, we present a weak null space property (wNSP) and prove that any sparse vector is a local minimizer of the $L_1 /L_2 $ model provided with this wNSP condition. Computationally, we focus on a constrained formulation that can be solved via the alternating direction method of multipliers (ADMM). Experiments show that the proposed approach is comparable to the state-of-the-art methods in sparse recovery. In addition, a variant of the $L_1/L_2$ model to apply on the gradient is also discussed with a proof-of-concept example of MRI reconstruction.construction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge