A Scale Invariant Approach for Sparse Signal Recovery

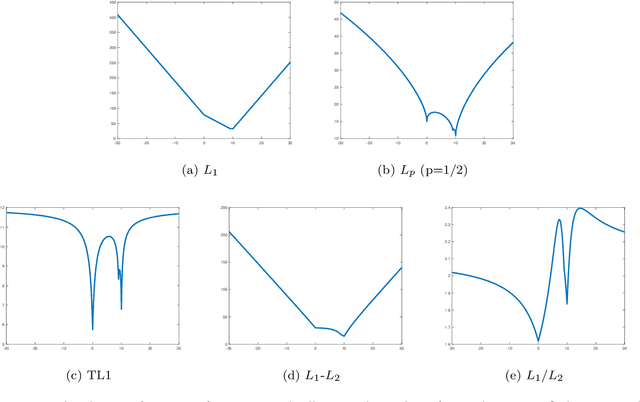
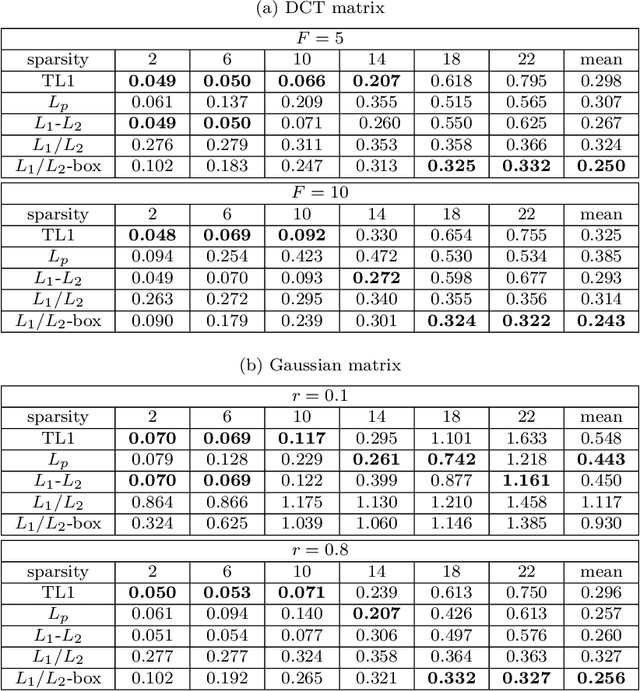
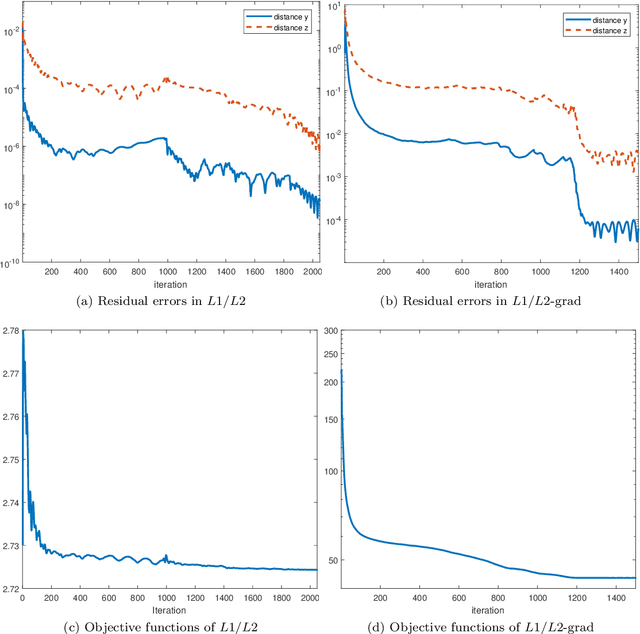
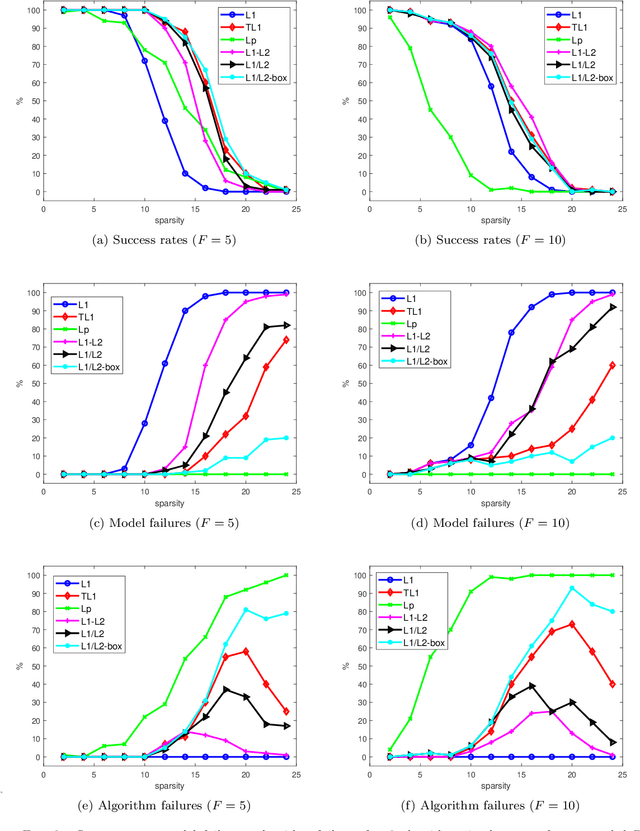
In this paper, we study the ratio of the $L_1 $ and $L_2 $ norms, denoted as $L_1/L_2$, to promote sparsity. Due to the non-convexity and non-linearity, there has been little attention to this scale-invariant metric. Compared to popular models in the literature such as the $L_p$ model for $p\in(0,1)$ and the transformed $L_1$ (TL1), this ratio model is parameter free. Theoretically, we present a weak null space property (wNSP) and prove that any sparse vector is a local minimizer of the $L_1 /L_2 $ model provided with this wNSP condition. Computationally, we focus on a constrained formulation that can be solved via the alternating direction method of multipliers (ADMM). Experiments show that the proposed approach is comparable to the state-of-the-art methods in sparse recovery. In addition, a variant of the $L_1/L_2$ model to apply on the gradient is also discussed with a proof-of-concept example of MRI reconstruction.construction.