Yifei Lou
Image Denoising Using Transformed L1 (TL1) Regularization via ADMM
Nov 19, 2025



Abstract:Total variation (TV) regularization is a classical tool for image denoising, but its convex $\ell_1$ formulation often leads to staircase artifacts and loss of contrast. To address these issues, we introduce the Transformed $\ell_1$ (TL1) regularizer applied to image gradients. In particular, we develop a TL1-regularized denoising model and solve it using the Alternating Direction Method of Multipliers (ADMM), featuring a closed-form TL1 proximal operator and an FFT-based image update under periodic boundary conditions. Experimental results demonstrate that our approach achieves superior denoising performance, effectively suppressing noise while preserving edges and enhancing image contrast.
A General Framework for Group Sparsity in Hyperspectral Unmixing Using Endmember Bundles
May 20, 2025Abstract:Due to low spatial resolution, hyperspectral data often consists of mixtures of contributions from multiple materials. This limitation motivates the task of hyperspectral unmixing (HU), a fundamental problem in hyperspectral imaging. HU aims to identify the spectral signatures (\textit{endmembers}) of the materials present in an observed scene, along with their relative proportions (\textit{fractional abundance}) in each pixel. A major challenge lies in the class variability in materials, which hinders accurate representation by a single spectral signature, as assumed in the conventional linear mixing model. Moreover, To address this issue, we propose using group sparsity after representing each material with a set of spectral signatures, known as endmember bundles, where each group corresponds to a specific material. In particular, we develop a bundle-based framework that can enforce either inter-group sparsity or sparsity within and across groups (SWAG) on the abundance coefficients. Furthermore, our framework offers the flexibility to incorporate a variety of sparsity-promoting penalties, among which the transformed $\ell_1$ (TL1) penalty is a novel regularization in the HU literature. Extensive experiments conducted on both synthetic and real hyperspectral data demonstrate the effectiveness and superiority of the proposed approaches.
Evidential Uncertainty Probes for Graph Neural Networks
Mar 11, 2025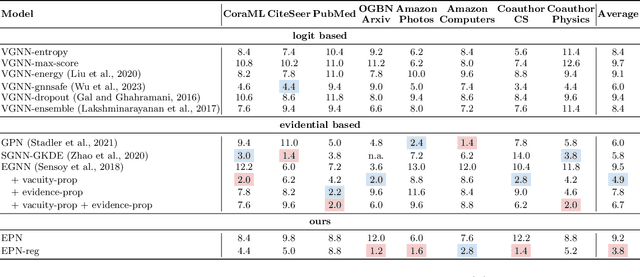
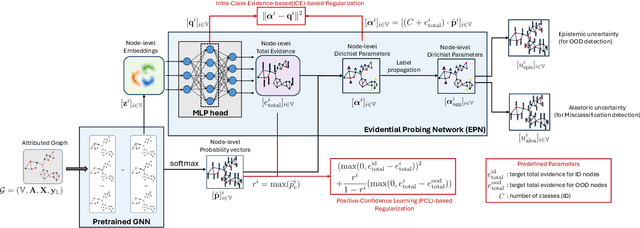
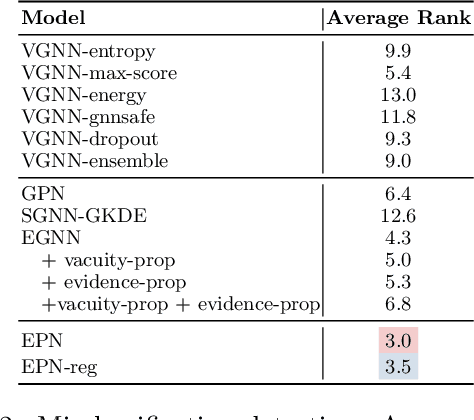
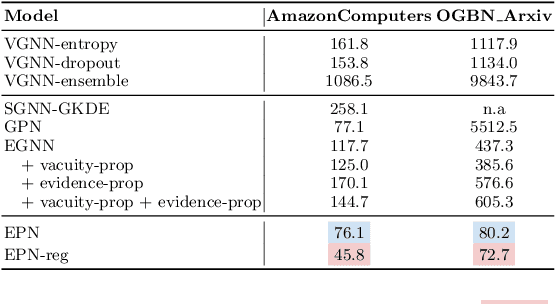
Abstract:Accurate quantification of both aleatoric and epistemic uncertainties is essential when deploying Graph Neural Networks (GNNs) in high-stakes applications such as drug discovery and financial fraud detection, where reliable predictions are critical. Although Evidential Deep Learning (EDL) efficiently quantifies uncertainty using a Dirichlet distribution over predictive probabilities, existing EDL-based GNN (EGNN) models require modifications to the network architecture and retraining, failing to take advantage of pre-trained models. We propose a plug-and-play framework for uncertainty quantification in GNNs that works with pre-trained models without the need for retraining. Our Evidential Probing Network (EPN) uses a lightweight Multi-Layer-Perceptron (MLP) head to extract evidence from learned representations, allowing efficient integration with various GNN architectures. We further introduce evidence-based regularization techniques, referred to as EPN-reg, to enhance the estimation of epistemic uncertainty with theoretical justifications. Extensive experiments demonstrate that the proposed EPN-reg achieves state-of-the-art performance in accurate and efficient uncertainty quantification, making it suitable for real-world deployment.
Time-Varying Graph Signal Recovery Using High-Order Smoothness and Adaptive Low-rankness
May 16, 2024

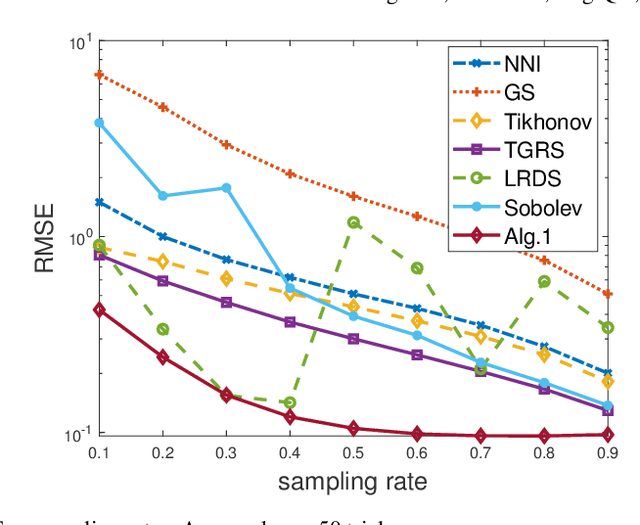
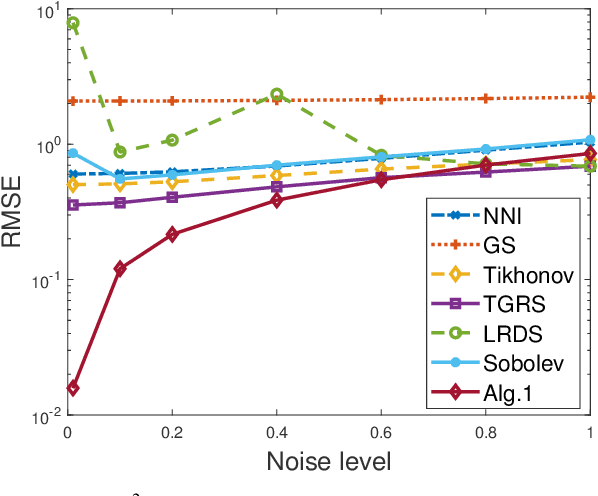
Abstract:Time-varying graph signal recovery has been widely used in many applications, including climate change, environmental hazard monitoring, and epidemic studies. It is crucial to choose appropriate regularizations to describe the characteristics of the underlying signals, such as the smoothness of the signal over the graph domain and the low-rank structure of the spatial-temporal signal modeled in a matrix form. As one of the most popular options, the graph Laplacian is commonly adopted in designing graph regularizations for reconstructing signals defined on a graph from partially observed data. In this work, we propose a time-varying graph signal recovery method based on the high-order Sobolev smoothness and an error-function weighted nuclear norm regularization to enforce the low-rankness. Two efficient algorithms based on the alternating direction method of multipliers and iterative reweighting are proposed, and convergence of one algorithm is shown in detail. We conduct various numerical experiments on synthetic and real-world data sets to demonstrate the proposed method's effectiveness compared to the state-of-the-art in graph signal recovery.
Improvements on Uncertainty Quantification for Node Classification via Distance-Based Regularization
Nov 10, 2023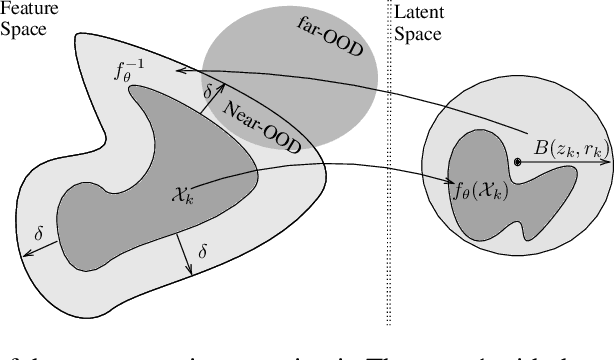
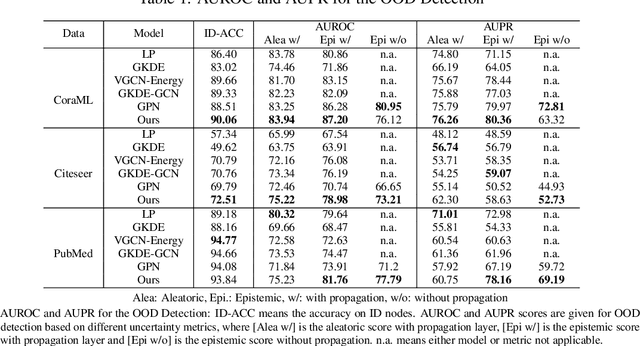

Abstract:Deep neural networks have achieved significant success in the last decades, but they are not well-calibrated and often produce unreliable predictions. A large number of literature relies on uncertainty quantification to evaluate the reliability of a learning model, which is particularly important for applications of out-of-distribution (OOD) detection and misclassification detection. We are interested in uncertainty quantification for interdependent node-level classification. We start our analysis based on graph posterior networks (GPNs) that optimize the uncertainty cross-entropy (UCE)-based loss function. We describe the theoretical limitations of the widely-used UCE loss. To alleviate the identified drawbacks, we propose a distance-based regularization that encourages clustered OOD nodes to remain clustered in the latent space. We conduct extensive comparison experiments on eight standard datasets and demonstrate that the proposed regularization outperforms the state-of-the-art in both OOD detection and misclassification detection.
Weighted Anisotropic-Isotropic Total Variation for Poisson Denoising
Jul 01, 2023Abstract:Poisson noise commonly occurs in images captured by photon-limited imaging systems such as in astronomy and medicine. As the distribution of Poisson noise depends on the pixel intensity value, noise levels vary from pixels to pixels. Hence, denoising a Poisson-corrupted image while preserving important details can be challenging. In this paper, we propose a Poisson denoising model by incorporating the weighted anisotropic-isotropic total variation (AITV) as a regularization. We then develop an alternating direction method of multipliers with a combination of a proximal operator for an efficient implementation. Lastly, numerical experiments demonstrate that our algorithm outperforms other Poisson denoising methods in terms of image quality and computational efficiency.
Non-convex approaches for low-rank tensor completion under tubal sampling
Mar 17, 2023



Abstract:Tensor completion is an important problem in modern data analysis. In this work, we investigate a specific sampling strategy, referred to as tubal sampling. We propose two novel non-convex tensor completion frameworks that are easy to implement, named tensor $L_1$-$L_2$ (TL12) and tensor completion via CUR (TCCUR). We test the efficiency of both methods on synthetic data and a color image inpainting problem. Empirical results reveal a trade-off between the accuracy and time efficiency of these two methods in a low sampling ratio. Each of them outperforms some classical completion methods in at least one aspect.
Efficient Image Segmentation Framework with Difference of Anisotropic and Isotropic Total Variation for Blur and Poisson Noise Removal
Jan 12, 2023
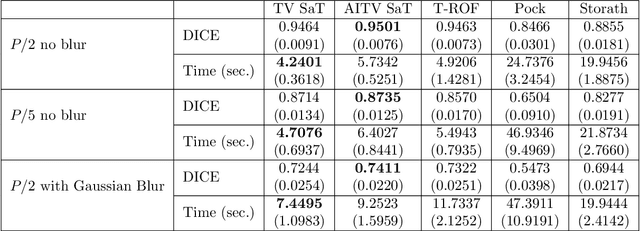

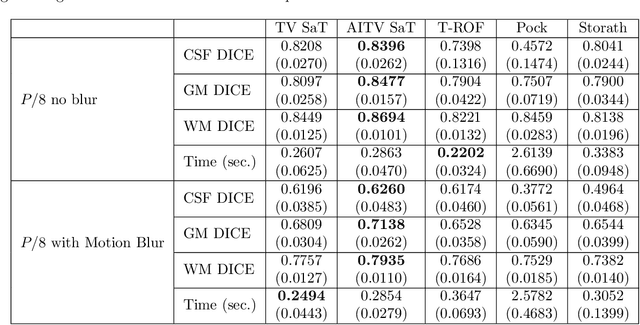
Abstract:In this paper, we aim to segment an image degraded by blur and Poisson noise. We adopt a smoothing-and-thresholding (SaT) segmentation framework that finds a piecewise-smooth solution, followed by $k$-means clustering to segment the image. Specifically for the image smoothing step, we replace the least-squares fidelity for Gaussian noise in the Mumford-Shah model with a maximum posterior (MAP) term to deal with Poisson noise and we incorporate the weighted difference of anisotropic and isotropic total variation (AITV) as a regularization to promote the sparsity of image gradients. For such a nonconvex model, we develop a specific splitting scheme and utilize a proximal operator to apply the alternating direction method of multipliers (ADMM). Convergence analysis is provided to validate the efficacy of the ADMM scheme. Numerical experiments on various segmentation scenarios (grayscale/color and multiphase) showcase that our proposed method outperforms a number of segmentation methods, including the original SaT.
A Smoothing and Thresholding Image Segmentation Framework with Weighted Anisotropic-Isotropic Total Variation
Mar 20, 2022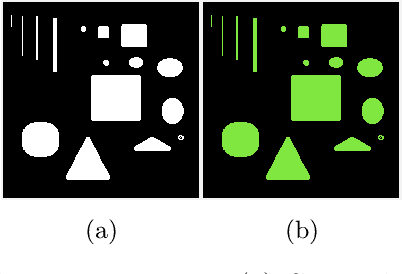
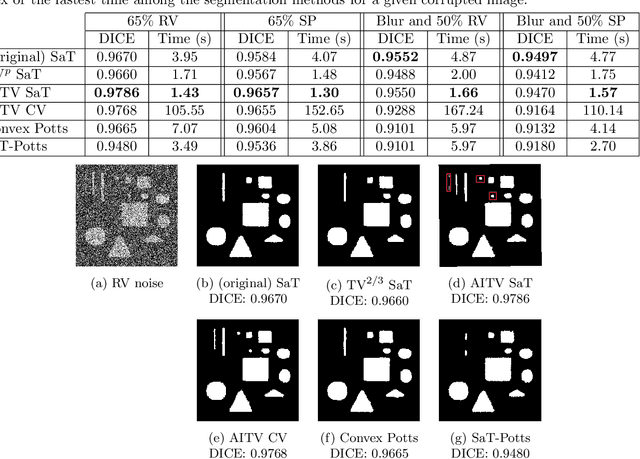

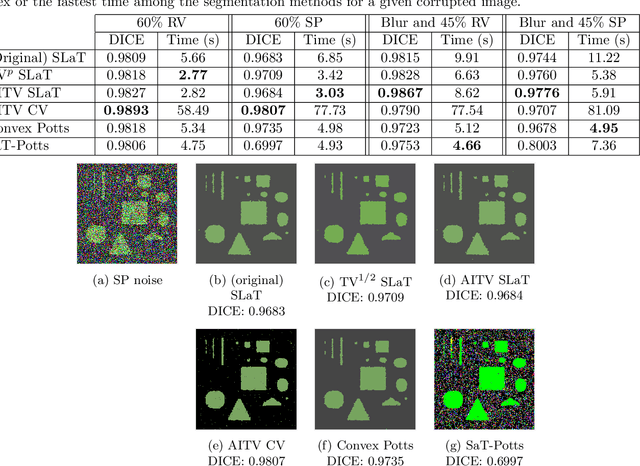
Abstract:In this paper, we propose a multi-stage image segmentation framework that incorporates a weighted difference of anisotropic and isotropic total variation (AITV). The segmentation framework generally consists of two stages: smoothing and thresholding, thus referred to as SaT. In the first stage, a smoothed image is obtained by an AITV-regularized Mumford-Shah (MS) model, which can be solved efficiently by the alternating direction method of multipliers (ADMM) with a closed-form solution of a proximal operator of the $\ell_1 -\alpha \ell_2$ regularizer. Convergence of the ADMM algorithm is analyzed. In the second stage, we threshold the smoothed image by $k$-means clustering to obtain the final segmentation result. Numerical experiments demonstrate that the proposed segmentation framework is versatile for both grayscale and color images, efficient in producing high-quality segmentation results within a few seconds, and robust to input images that are corrupted with noise, blur, or both. We compare the AITV method with its original convex and nonconvex TV$^p (0<p<1)$ counterparts, showcasing the qualitative and quantitative advantages of our proposed method.
A Lifted $\ell_1 $ Framework for Sparse Recovery
Mar 10, 2022



Abstract:Motivated by re-weighted $\ell_1$ approaches for sparse recovery, we propose a lifted $\ell_1$ (LL1) regularization which is a generalized form of several popular regularizations in the literature. By exploring such connections, we discover there are two types of lifting functions which can guarantee that the proposed approach is equivalent to the $\ell_0$ minimization. Computationally, we design an efficient algorithm via the alternating direction method of multiplier (ADMM) and establish the convergence for an unconstrained formulation. Experimental results are presented to demonstrate how this generalization improves sparse recovery over the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge