A Dual Basis Approach for Structured Robust Euclidean Distance Geometry

Euclidean Distance Matrix (EDM), which consists of pairwise squared Euclidean distances of a given point configuration, finds many applications in modern machine learning. This paper considers the setting where only a set of anchor nodes is used to collect the distances between themselves and the rest. In the presence of potential outliers, it results in a structured partial observation on EDM with partial corruptions. Note that an EDM can be connected to a positive semi-definite Gram matrix via a non-orthogonal dual basis. Inspired by recent development of non-orthogonal dual basis in optimization, we propose a novel algorithmic framework, dubbed Robust Euclidean Distance Geometry via Dual Basis (RoDEoDB), for recovering the Euclidean distance geometry, i.e., the underlying point configuration. The exact recovery guarantees have been established in terms of both the Gram matrix and point configuration, under some mild conditions. Empirical experiments show superior performance of RoDEoDB on sensor localization and molecular conformation datasets.

Property Inheritance for Subtensors in Tensor Train Decompositions

Tensor dimensionality reduction is one of the fundamental tools for modern data science. To address the high computational overhead, fiber-wise sampled subtensors that preserve the original tensor rank are often used in designing efficient and scalable tensor dimensionality reduction. However, the theory of property inheritance for subtensors is still underdevelopment, that is, how the essential properties of the original tensor will be passed to its subtensors. This paper theoretically studies the property inheritance of the two key tensor properties, namely incoherence and condition number, under the tensor train setting. We also show how tensor train rank is preserved through fiber-wise sampling. The key parameters introduced in theorems are numerically evaluated under various settings. The results show that the properties of interest can be well preserved to the subtensors formed via fiber-wise sampling. Overall, this paper provides several handy analytic tools for developing efficient tensor analysis

Explainable Adversarial Attacks on Coarse-to-Fine Classifiers

Traditional adversarial attacks typically aim to alter the predicted labels of input images by generating perturbations that are imperceptible to the human eye. However, these approaches often lack explainability. Moreover, most existing work on adversarial attacks focuses on single-stage classifiers, but multi-stage classifiers are largely unexplored. In this paper, we introduce instance-based adversarial attacks for multi-stage classifiers, leveraging Layer-wise Relevance Propagation (LRP), which assigns relevance scores to pixels based on their influence on classification outcomes. Our approach generates explainable adversarial perturbations by utilizing LRP to identify and target key features critical for both coarse and fine-grained classifications. Unlike conventional attacks, our method not only induces misclassification but also enhances the interpretability of the model's behavior across classification stages, as demonstrated by experimental results.

Deeply Learned Robust Matrix Completion for Large-scale Low-rank Data Recovery

Robust matrix completion (RMC) is a widely used machine learning tool that simultaneously tackles two critical issues in low-rank data analysis: missing data entries and extreme outliers. This paper proposes a novel scalable and learnable non-convex approach, coined Learned Robust Matrix Completion (LRMC), for large-scale RMC problems. LRMC enjoys low computational complexity with linear convergence. Motivated by the proposed theorem, the free parameters of LRMC can be effectively learned via deep unfolding to achieve optimum performance. Furthermore, this paper proposes a flexible feedforward-recurrent-mixed neural network framework that extends deep unfolding from fix-number iterations to infinite iterations. The superior empirical performance of LRMC is verified with extensive experiments against state-of-the-art on synthetic datasets and real applications, including video background subtraction, ultrasound imaging, face modeling, and cloud removal from satellite imagery.

Structured Sampling for Robust Euclidean Distance Geometry

This paper addresses the problem of estimating the positions of points from distance measurements corrupted by sparse outliers. Specifically, we consider a setting with two types of nodes: anchor nodes, for which exact distances to each other are known, and target nodes, for which complete but corrupted distance measurements to the anchors are available. To tackle this problem, we propose a novel algorithm powered by Nystr\"om method and robust principal component analysis. Our method is computationally efficient as it processes only a localized subset of the distance matrix and does not require distance measurements between target nodes. Empirical evaluations on synthetic datasets, designed to mimic sensor localization, and on molecular experiments, demonstrate that our algorithm achieves accurate recovery with a modest number of anchors, even in the presence of high levels of sparse outliers.

Guarantees of a Preconditioned Subgradient Algorithm for Overparameterized Asymmetric Low-rank Matrix Recovery

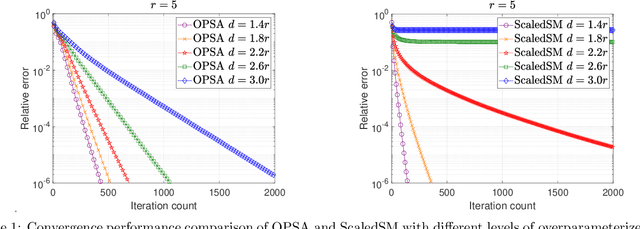
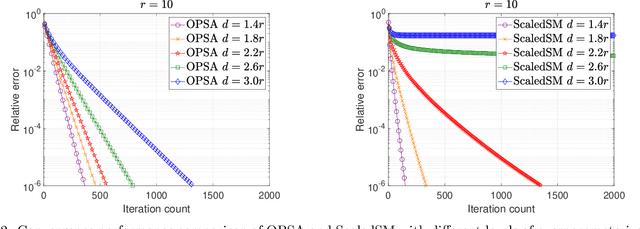
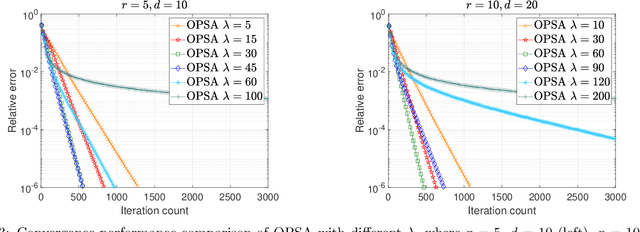
In this paper, we focus on a matrix factorization-based approach for robust low-rank and asymmetric matrix recovery from corrupted measurements. We address the challenging scenario where the rank of the sought matrix is unknown and employ an overparameterized approach using the variational form of the nuclear norm as a regularizer. We propose a subgradient algorithm that inherits the merits of preconditioned algorithms, whose rate of convergence does not depend on the condition number of the sought matrix, and addresses their current limitation, i.e., the lack of convergence guarantees in the case of asymmetric matrices with unknown rank. In this setting, we provide, for the first time in the literature, linear convergence guarantees for the derived overparameterized preconditioned subgradient algorithm in the presence of gross corruptions. Additionally, by applying our approach to matrix sensing, we highlight its merits when the measurement operator satisfies the mixed-norm restricted isometry properties. Lastly, we present numerical experiments that validate our theoretical results and demonstrate the effectiveness of our approach.

Riemannian Optimization for Non-convex Euclidean Distance Geometry with Global Recovery Guarantees

The problem of determining the configuration of points from partial distance information, known as the Euclidean Distance Geometry (EDG) problem, is fundamental to many tasks in the applied sciences. In this paper, we propose two algorithms grounded in the Riemannian optimization framework to address the EDG problem. Our approach formulates the problem as a low-rank matrix completion task over the Gram matrix, using partial measurements represented as expansion coefficients of the Gram matrix in a non-orthogonal basis. For the first algorithm, under a uniform sampling with replacement model for the observed distance entries, we demonstrate that, with high probability, a Riemannian gradient-like algorithm on the manifold of rank-$r$ matrices converges linearly to the true solution, given initialization via a one-step hard thresholding. This holds provided the number of samples, $m$, satisfies $m \geq \mathcal{O}(n^{7/4}r^2 \log(n))$. With a more refined initialization, achieved through resampled Riemannian gradient-like descent, we further improve this bound to $m \geq \mathcal{O}(nr^2 \log(n))$. Our analysis for the first algorithm leverages a non-self-adjoint operator and depends on deriving eigenvalue bounds for an inner product matrix of restricted basis matrices, leveraging sparsity properties for tighter guarantees than previously established. The second algorithm introduces a self-adjoint surrogate for the sampling operator. This algorithm demonstrates strong numerical performance on both synthetic and real data. Furthermore, we show that optimizing over manifolds of higher-than-rank-$r$ matrices yields superior numerical results, consistent with recent literature on overparameterization in the EDG problem.

Correlating Time Series with Interpretable Convolutional Kernels

This study addresses the problem of convolutional kernel learning in univariate, multivariate, and multidimensional time series data, which is crucial for interpreting temporal patterns in time series and supporting downstream machine learning tasks. First, we propose formulating convolutional kernel learning for univariate time series as a sparse regression problem with a non-negative constraint, leveraging the properties of circular convolution and circulant matrices. Second, to generalize this approach to multivariate and multidimensional time series data, we use tensor computations, reformulating the convolutional kernel learning problem in the form of tensors. This is further converted into a standard sparse regression problem through vectorization and tensor unfolding operations. In the proposed methodology, the optimization problem is addressed using the existing non-negative subspace pursuit method, enabling the convolutional kernel to capture temporal correlations and patterns. To evaluate the proposed model, we apply it to several real-world time series datasets. On the multidimensional rideshare and taxi trip data from New York City and Chicago, the convolutional kernels reveal interpretable local correlations and cyclical patterns, such as weekly seasonality. In the context of multidimensional fluid flow data, both local and nonlocal correlations captured by the convolutional kernels can reinforce tensor factorization, leading to performance improvements in fluid flow reconstruction tasks. Thus, this study lays an insightful foundation for automatically learning convolutional kernels from time series data, with an emphasis on interpretability through sparsity and non-negativity constraints.

S$^3$Attention: Improving Long Sequence Attention with Smoothed Skeleton Sketching

Attention based models have achieved many remarkable breakthroughs in numerous applications. However, the quadratic complexity of Attention makes the vanilla Attention based models hard to apply to long sequence tasks. Various improved Attention structures are proposed to reduce the computation cost by inducing low rankness and approximating the whole sequence by sub-sequences. The most challenging part of those approaches is maintaining the proper balance between information preservation and computation reduction: the longer sub-sequences used, the better information is preserved, but at the price of introducing more noise and computational costs. In this paper, we propose a smoothed skeleton sketching based Attention structure, coined S$^3$Attention, which significantly improves upon the previous attempts to negotiate this trade-off. S$^3$Attention has two mechanisms to effectively minimize the impact of noise while keeping the linear complexity to the sequence length: a smoothing block to mix information over long sequences and a matrix sketching method that simultaneously selects columns and rows from the input matrix. We verify the effectiveness of S$^3$Attention both theoretically and empirically. Extensive studies over Long Range Arena (LRA) datasets and six time-series forecasting show that S$^3$Attention significantly outperforms both vanilla Attention and other state-of-the-art variants of Attention structures.

Guaranteed Sampling Flexibility for Low-tubal-rank Tensor Completion

While Bernoulli sampling is extensively studied in tensor completion, t-CUR sampling approximates low-tubal-rank tensors via lateral and horizontal subtensors. However, both methods lack sufficient flexibility for diverse practical applications. To address this, we introduce Tensor Cross-Concentrated Sampling (t-CCS), a novel and straightforward sampling model that advances the matrix cross-concentrated sampling concept within a tensor framework. t-CCS effectively bridges the gap between Bernoulli and t-CUR sampling, offering additional flexibility that can lead to computational savings in various contexts. A key aspect of our work is the comprehensive theoretical analysis provided. We establish a sufficient condition for the successful recovery of a low-rank tensor from its t-CCS samples. In support of this, we also develop a theoretical framework validating the feasibility of t-CUR via uniform random sampling and conduct a detailed theoretical sampling complexity analysis for tensor completion problems utilizing the general Bernoulli sampling model. Moreover, we introduce an efficient non-convex algorithm, the Iterative t-CUR Tensor Completion (ITCURTC) algorithm, specifically designed to tackle the t-CCS-based tensor completion. We have intensively tested and validated the effectiveness of the t-CCS model and the ITCURTC algorithm across both synthetic and real-world datasets.