Exploration vs Exploitation: Rethinking RLVR through Clipping, Entropy, and Spurious Reward

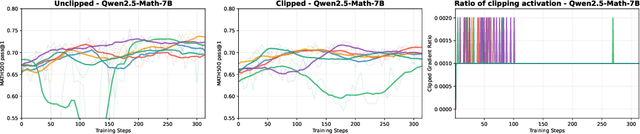
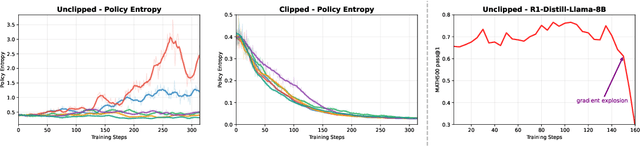
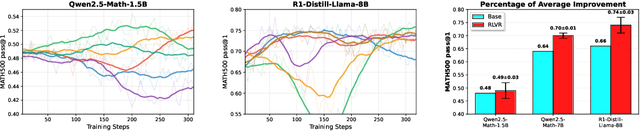
This paper examines the exploration-exploitation trade-off in reinforcement learning with verifiable rewards (RLVR), a framework for improving the reasoning of Large Language Models (LLMs). Recent studies suggest that RLVR can elicit strong mathematical reasoning in LLMs through two seemingly paradoxical mechanisms: spurious rewards, which suppress exploitation by rewarding outcomes unrelated to the ground truth, and entropy minimization, which suppresses exploration by pushing the model toward more confident and deterministic outputs, highlighting a puzzling dynamic: both discouraging exploitation and discouraging exploration improve reasoning performance, yet the underlying principles that reconcile these effects remain poorly understood. We focus on two fundamental questions: (i) how policy entropy relates to performance, and (ii) whether spurious rewards yield gains, potentially through the interplay of clipping bias and model contamination. Our results show that clipping bias under spurious rewards reduces policy entropy, leading to more confident and deterministic outputs, while entropy minimization alone is insufficient for improvement. We further propose a reward-misalignment model explaining why spurious rewards can enhance performance beyond contaminated settings. Our findings clarify the mechanisms behind spurious-reward benefits and provide principles for more effective RLVR training.

ComPO: Preference Alignment via Comparison Oracles

Direct alignment methods are increasingly used for aligning large language models (LLMs) with human preferences. However, these methods suffer from the issues of verbosity and likelihood displacement, which can be driven by the noisy preference pairs that induce similar likelihood for preferred and dispreferred responses. The contributions of this paper are two-fold. First, we propose a new preference alignment method based on comparison oracles and provide the convergence guarantee for its basic scheme. Second, we improve our method using some heuristics and conduct the experiments to demonstrate the flexibility and compatibility of practical scheme in improving the performance of LLMs using noisy preference pairs. Evaluations are conducted across multiple base and instruction-tuned models (Mistral-7B, Llama-3-8B and Gemma-2-9B) with benchmarks (AlpacaEval 2, MT-Bench and Arena-Hard). Experimental results show the effectiveness of our method as an alternative to addressing the limitations of existing direct alignment methods. A highlight of our work is that we evidence the importance of designing specialized methods for preference pairs with distinct likelihood margin, which complements the recent findings in \citet{Razin-2025-Unintentional}.

SymAgent: A Neural-Symbolic Self-Learning Agent Framework for Complex Reasoning over Knowledge Graphs

Recent advancements have highlighted that Large Language Models (LLMs) are prone to hallucinations when solving complex reasoning problems, leading to erroneous results. To tackle this issue, researchers incorporate Knowledge Graphs (KGs) to improve the reasoning ability of LLMs. However, existing methods face two limitations: 1) they typically assume that all answers to the questions are contained in KGs, neglecting the incompleteness issue of KGs, and 2) they treat the KG as a static repository and overlook the implicit logical reasoning structures inherent in KGs. In this paper, we introduce SymAgent, an innovative neural-symbolic agent framework that achieves collaborative augmentation between KGs and LLMs. We conceptualize KGs as dynamic environments and transform complex reasoning tasks into a multi-step interactive process, enabling KGs to participate deeply in the reasoning process. SymAgent consists of two modules: Agent-Planner and Agent-Executor. The Agent-Planner leverages LLM's inductive reasoning capability to extract symbolic rules from KGs, guiding efficient question decomposition. The Agent-Executor autonomously invokes predefined action tools to integrate information from KGs and external documents, addressing the issues of KG incompleteness. Furthermore, we design a self-learning framework comprising online exploration and offline iterative policy updating phases, enabling the agent to automatically synthesize reasoning trajectories and improve performance. Experimental results demonstrate that SymAgent with weak LLM backbones (i.e., 7B series) yields better or comparable performance compared to various strong baselines. Further analysis reveals that our agent can identify missing triples, facilitating automatic KG updates.

Deeply Learned Robust Matrix Completion for Large-scale Low-rank Data Recovery

Robust matrix completion (RMC) is a widely used machine learning tool that simultaneously tackles two critical issues in low-rank data analysis: missing data entries and extreme outliers. This paper proposes a novel scalable and learnable non-convex approach, coined Learned Robust Matrix Completion (LRMC), for large-scale RMC problems. LRMC enjoys low computational complexity with linear convergence. Motivated by the proposed theorem, the free parameters of LRMC can be effectively learned via deep unfolding to achieve optimum performance. Furthermore, this paper proposes a flexible feedforward-recurrent-mixed neural network framework that extends deep unfolding from fix-number iterations to infinite iterations. The superior empirical performance of LRMC is verified with extensive experiments against state-of-the-art on synthetic datasets and real applications, including video background subtraction, ultrasound imaging, face modeling, and cloud removal from satellite imagery.

S$^3$Attention: Improving Long Sequence Attention with Smoothed Skeleton Sketching

Attention based models have achieved many remarkable breakthroughs in numerous applications. However, the quadratic complexity of Attention makes the vanilla Attention based models hard to apply to long sequence tasks. Various improved Attention structures are proposed to reduce the computation cost by inducing low rankness and approximating the whole sequence by sub-sequences. The most challenging part of those approaches is maintaining the proper balance between information preservation and computation reduction: the longer sub-sequences used, the better information is preserved, but at the price of introducing more noise and computational costs. In this paper, we propose a smoothed skeleton sketching based Attention structure, coined S$^3$Attention, which significantly improves upon the previous attempts to negotiate this trade-off. S$^3$Attention has two mechanisms to effectively minimize the impact of noise while keeping the linear complexity to the sequence length: a smoothing block to mix information over long sequences and a matrix sketching method that simultaneously selects columns and rows from the input matrix. We verify the effectiveness of S$^3$Attention both theoretically and empirically. Extensive studies over Long Range Arena (LRA) datasets and six time-series forecasting show that S$^3$Attention significantly outperforms both vanilla Attention and other state-of-the-art variants of Attention structures.

Solving General Natural-Language-Description Optimization Problems with Large Language Models

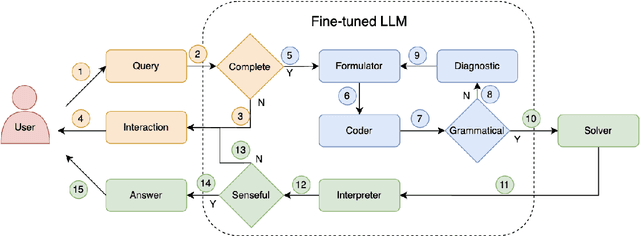
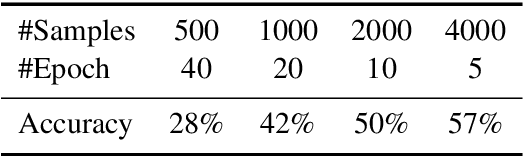
Optimization problems seek to find the best solution to an objective under a set of constraints, and have been widely investigated in real-world applications. Modeling and solving optimization problems in a specific domain typically require a combination of domain knowledge, mathematical skills, and programming ability, making it difficult for general users and even domain professionals. In this paper, we propose a novel framework called OptLLM that augments LLMs with external solvers. Specifically, OptLLM accepts user queries in natural language, convert them into mathematical formulations and programming codes, and calls the solvers to calculate the results for decision-making. In addition, OptLLM supports multi-round dialogues to gradually refine the modeling and solving of optimization problems. To illustrate the effectiveness of OptLLM, we provide tutorials on three typical optimization applications and conduct experiments on both prompt-based GPT models and a fine-tuned Qwen model using a large-scale selfdeveloped optimization dataset. Experimental results show that OptLLM works with various LLMs, and the fine-tuned model achieves an accuracy boost compared to the promptbased models. Some features of OptLLM framework have been available for trial since June 2023 (https://opt.alibabacloud.com/chat or https://opt.aliyun.com/chat).

Expressive Power of Graph Neural Networks for Quadratic Programs

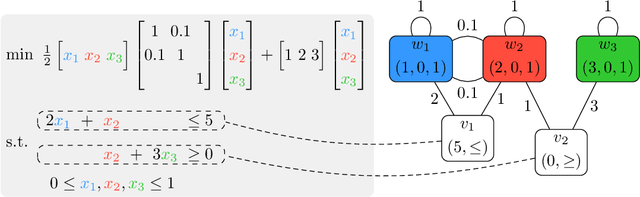
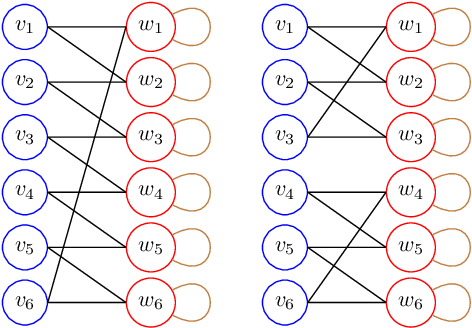
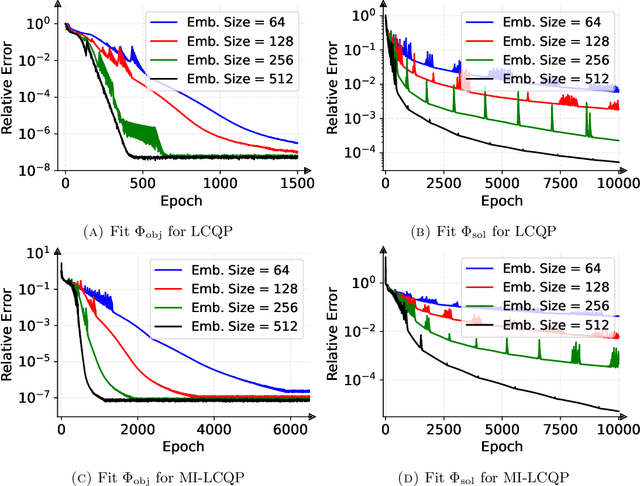
Quadratic programming (QP) is the most widely applied category of problems in nonlinear programming. Many applications require real-time/fast solutions, though not necessarily with high precision. Existing methods either involve matrix decomposition or use the preconditioned conjugate gradient method. For relatively large instances, these methods cannot achieve the real-time requirement unless there is an effective precondition. Recently, graph neural networks (GNNs) opened new possibilities for QP. Some promising empirical studies of applying GNNs for QP tasks show that GNNs can capture key characteristics of an optimization instance and provide adaptive guidance accordingly to crucial configurations during the solving process, or directly provide an approximate solution. Despite notable empirical observations, theoretical foundations are still lacking. In this work, we investigate the expressive or representative power of GNNs, a crucial aspect of neural network theory, specifically in the context of QP tasks, with both continuous and mixed-integer settings. We prove the existence of message-passing GNNs that can reliably represent key properties of quadratic programs, including feasibility, optimal objective value, and optimal solution. Our theory is validated by numerical results.

ODE-based Learning to Optimize

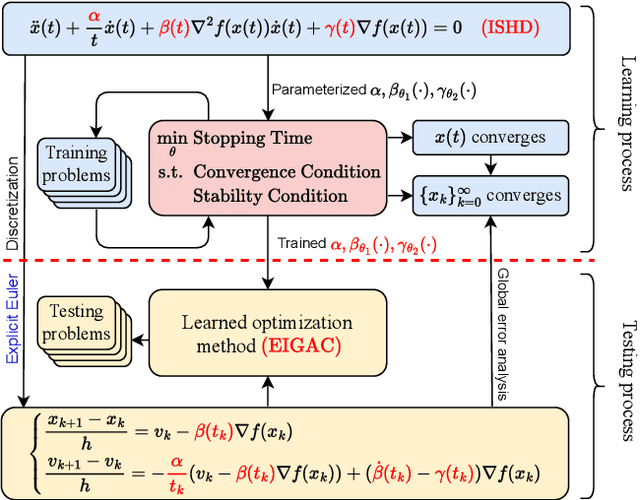
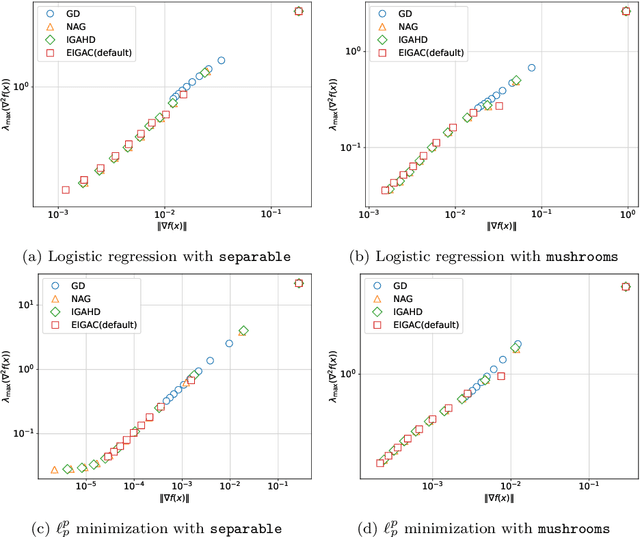
Recent years have seen a growing interest in understanding acceleration methods through the lens of ordinary differential equations (ODEs). Despite the theoretical advancements, translating the rapid convergence observed in continuous-time models to discrete-time iterative methods poses significant challenges. In this paper, we present a comprehensive framework integrating the inertial systems with Hessian-driven damping equation (ISHD) and learning-based approaches for developing optimization methods through a deep synergy of theoretical insights. We first establish the convergence condition for ensuring the convergence of the solution trajectory of ISHD. Then, we show that provided the stability condition, another relaxed requirement on the coefficients of ISHD, the sequence generated through the explicit Euler discretization of ISHD converges, which gives a large family of practical optimization methods. In order to select the best optimization method in this family for certain problems, we introduce the stopping time, the time required for an optimization method derived from ISHD to achieve a predefined level of suboptimality. Then, we formulate a novel learning to optimize (L2O) problem aimed at minimizing the stopping time subject to the convergence and stability condition. To navigate this learning problem, we present an algorithm combining stochastic optimization and the penalty method (StoPM). The convergence of StoPM using the conservative gradient is proved. Empirical validation of our framework is conducted through extensive numerical experiments across a diverse set of optimization problems. These experiments showcase the superior performance of the learned optimization methods.

Learning to optimize: A tutorial for continuous and mixed-integer optimization

Learning to Optimize (L2O) stands at the intersection of traditional optimization and machine learning, utilizing the capabilities of machine learning to enhance conventional optimization techniques. As real-world optimization problems frequently share common structures, L2O provides a tool to exploit these structures for better or faster solutions. This tutorial dives deep into L2O techniques, introducing how to accelerate optimization algorithms, promptly estimate the solutions, or even reshape the optimization problem itself, making it more adaptive to real-world applications. By considering the prerequisites for successful applications of L2O and the structure of the optimization problems at hand, this tutorial provides a comprehensive guide for practitioners and researchers alike.

Bagging Improves Generalization Exponentially

Bagging is a popular ensemble technique to improve the accuracy of machine learning models. It hinges on the well-established rationale that, by repeatedly retraining on resampled data, the aggregated model exhibits lower variance and hence higher stability, especially for discontinuous base learners. In this paper, we provide a new perspective on bagging: By suitably aggregating the base learners at the parametrization instead of the output level, bagging improves generalization performances exponentially, a strength that is significantly more powerful than variance reduction. More precisely, we show that for general stochastic optimization problems that suffer from slowly (i.e., polynomially) decaying generalization errors, bagging can effectively reduce these errors to an exponential decay. Moreover, this power of bagging is agnostic to the solution schemes, including common empirical risk minimization, distributionally robust optimization, and various regularizations. We demonstrate how bagging can substantially improve generalization performances in a range of examples involving heavy-tailed data that suffer from intrinsically slow rates.