Chasing Better Deep Image Priors between Over- and Under-parameterization

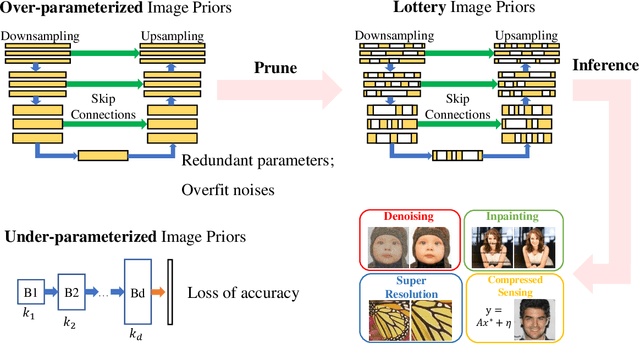
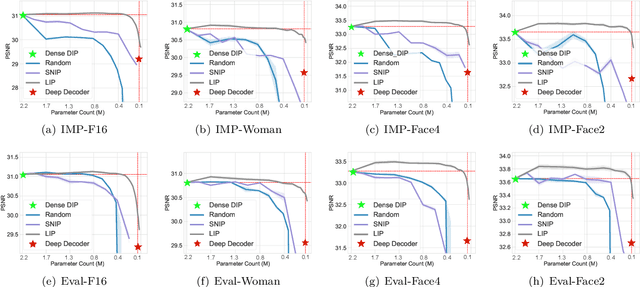
Deep Neural Networks (DNNs) are well-known to act as over-parameterized deep image priors (DIP) that regularize various image inverse problems. Meanwhile, researchers also proposed extremely compact, under-parameterized image priors (e.g., deep decoder) that are strikingly competent for image restoration too, despite a loss of accuracy. These two extremes push us to think whether there exists a better solution in the middle: between over- and under-parameterized image priors, can one identify "intermediate" parameterized image priors that achieve better trade-offs between performance, efficiency, and even preserving strong transferability? Drawing inspirations from the lottery ticket hypothesis (LTH), we conjecture and study a novel "lottery image prior" (LIP) by exploiting DNN inherent sparsity, stated as: given an over-parameterized DNN-based image prior, it will contain a sparse subnetwork that can be trained in isolation, to match the original DNN's performance when being applied as a prior to various image inverse problems. Our results validate the superiority of LIPs: we can successfully locate the LIP subnetworks from over-parameterized DIPs at substantial sparsity ranges. Those LIP subnetworks significantly outperform deep decoders under comparably compact model sizes (by often fully preserving the effectiveness of their over-parameterized counterparts), and they also possess high transferability across different images as well as restoration task types. Besides, we also extend LIP to compressive sensing image reconstruction, where a pre-trained GAN generator is used as the prior (in contrast to untrained DIP or deep decoder), and confirm its validity in this setting too. To our best knowledge, this is the first time that LTH is demonstrated to be relevant in the context of inverse problems or image priors.

Expressive Power of Graph Neural Networks for Quadratic Programs

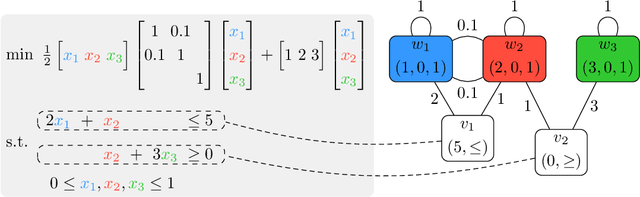
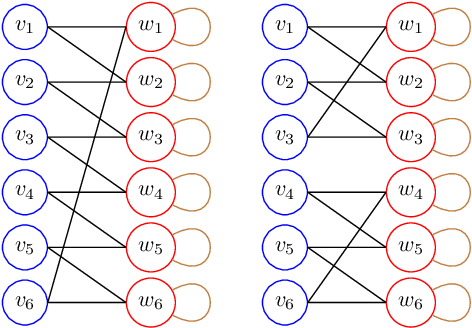
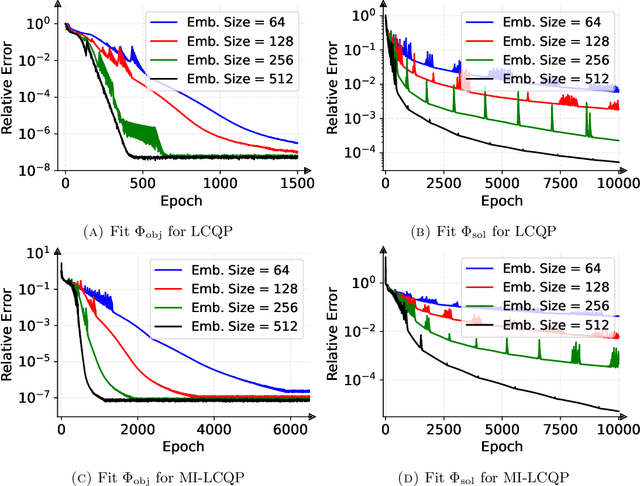
Quadratic programming (QP) is the most widely applied category of problems in nonlinear programming. Many applications require real-time/fast solutions, though not necessarily with high precision. Existing methods either involve matrix decomposition or use the preconditioned conjugate gradient method. For relatively large instances, these methods cannot achieve the real-time requirement unless there is an effective precondition. Recently, graph neural networks (GNNs) opened new possibilities for QP. Some promising empirical studies of applying GNNs for QP tasks show that GNNs can capture key characteristics of an optimization instance and provide adaptive guidance accordingly to crucial configurations during the solving process, or directly provide an approximate solution. Despite notable empirical observations, theoretical foundations are still lacking. In this work, we investigate the expressive or representative power of GNNs, a crucial aspect of neural network theory, specifically in the context of QP tasks, with both continuous and mixed-integer settings. We prove the existence of message-passing GNNs that can reliably represent key properties of quadratic programs, including feasibility, optimal objective value, and optimal solution. Our theory is validated by numerical results.

Learning to optimize: A tutorial for continuous and mixed-integer optimization

Learning to Optimize (L2O) stands at the intersection of traditional optimization and machine learning, utilizing the capabilities of machine learning to enhance conventional optimization techniques. As real-world optimization problems frequently share common structures, L2O provides a tool to exploit these structures for better or faster solutions. This tutorial dives deep into L2O techniques, introducing how to accelerate optimization algorithms, promptly estimate the solutions, or even reshape the optimization problem itself, making it more adaptive to real-world applications. By considering the prerequisites for successful applications of L2O and the structure of the optimization problems at hand, this tutorial provides a comprehensive guide for practitioners and researchers alike.

Rethinking the Capacity of Graph Neural Networks for Branching Strategy

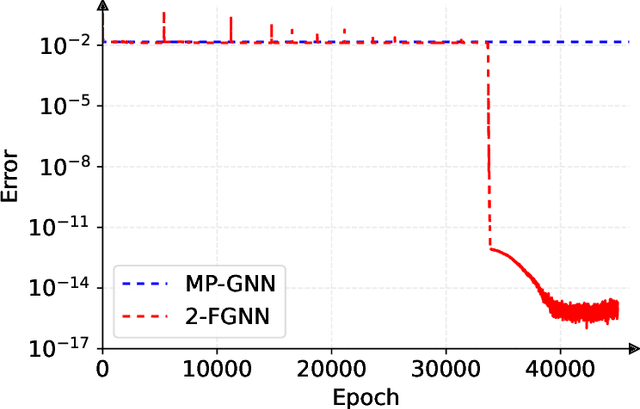
Graph neural networks (GNNs) have been widely used to predict properties and heuristics of mixed-integer linear programs (MILPs) and hence accelerate MILP solvers. This paper investigates the capacity of GNNs to represent strong branching (SB) scores that provide an efficient strategy in the branch-and-bound algorithm. Although message-passing GNN (MP-GNN), as the simplest GNN structure, is frequently employed in the existing literature to learn SB scores, we prove a fundamental limitation in its expressive power -- there exist two MILP instances with different SB scores that cannot be distinguished by any MP-GNN, regardless of the number of parameters. In addition, we establish a universal approximation theorem for another GNN structure called the second-order folklore GNN (2-FGNN). We show that for any data distribution over MILPs, there always exists a 2-FGNN that can approximate the SB score with arbitrarily high accuracy and arbitrarily high probability. A small-scale numerical experiment is conducted to directly validate our theoretical findings.

DIG-MILP: a Deep Instance Generator for Mixed-Integer Linear Programming with Feasibility Guarantee

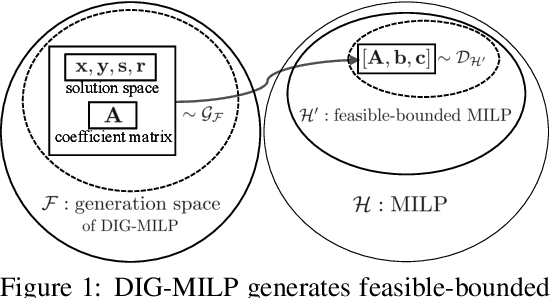
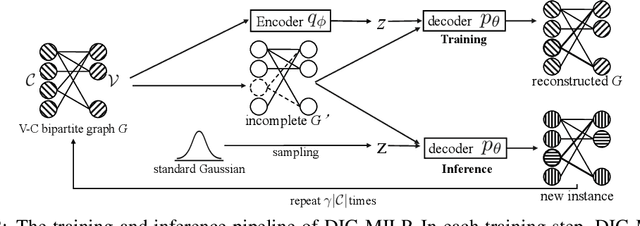
Mixed-integer linear programming (MILP) stands as a notable NP-hard problem pivotal to numerous crucial industrial applications. The development of effective algorithms, the tuning of solvers, and the training of machine learning models for MILP resolution all hinge on access to extensive, diverse, and representative data. Yet compared to the abundant naturally occurring data in image and text realms, MILP is markedly data deficient, underscoring the vital role of synthetic MILP generation. We present DIG-MILP, a deep generative framework based on variational auto-encoder (VAE), adept at extracting deep-level structural features from highly limited MILP data and producing instances that closely mirror the target data. Notably, by leveraging the MILP duality, DIG-MILP guarantees a correct and complete generation space as well as ensures the boundedness and feasibility of the generated instances. Our empirical study highlights the novelty and quality of the instances generated by DIG-MILP through two distinct downstream tasks: (S1) Data sharing, where solver solution times correlate highly positive between original and DIG-MILP-generated instances, allowing data sharing for solver tuning without publishing the original data; (S2) Data Augmentation, wherein the DIG-MILP-generated instances bolster the generalization performance of machine learning models tasked with resolving MILP problems.

Towards Constituting Mathematical Structures for Learning to Optimize

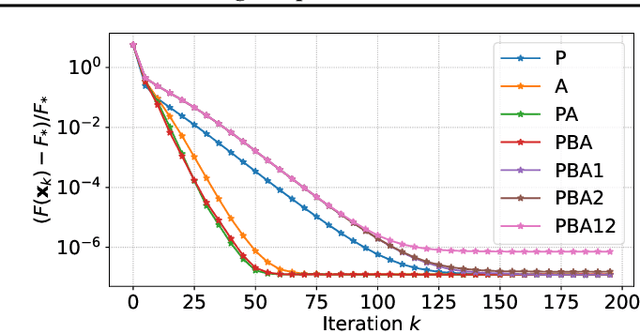
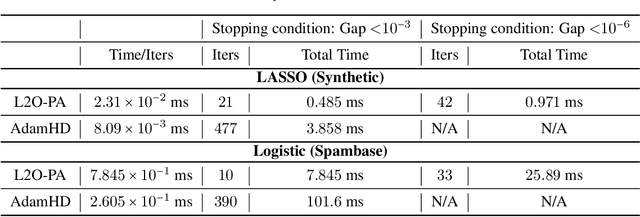
Learning to Optimize (L2O), a technique that utilizes machine learning to learn an optimization algorithm automatically from data, has gained arising attention in recent years. A generic L2O approach parameterizes the iterative update rule and learns the update direction as a black-box network. While the generic approach is widely applicable, the learned model can overfit and may not generalize well to out-of-distribution test sets. In this paper, we derive the basic mathematical conditions that successful update rules commonly satisfy. Consequently, we propose a novel L2O model with a mathematics-inspired structure that is broadly applicable and generalized well to out-of-distribution problems. Numerical simulations validate our theoretical findings and demonstrate the superior empirical performance of the proposed L2O model.

More ConvNets in the 2020s: Scaling up Kernels Beyond 51x51 using Sparsity

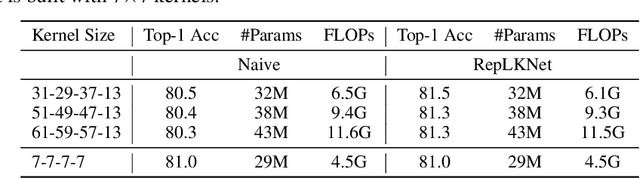
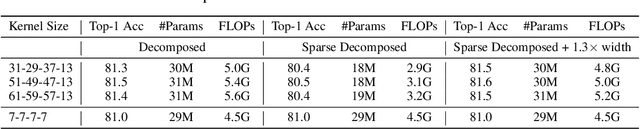
Transformers have quickly shined in the computer vision world since the emergence of Vision Transformers (ViTs). The dominant role of convolutional neural networks (CNNs) seems to be challenged by increasingly effective transformer-based models. Very recently, a couple of advanced convolutional models strike back with large kernels motivated by the local but large attention mechanism, showing appealing performance and efficiency. While one of them, i.e. RepLKNet, impressively manages to scale the kernel size to 31x31 with improved performance, the performance starts to saturate as the kernel size continues growing, compared to the scaling trend of advanced ViTs such as Swin Transformer. In this paper, we explore the possibility of training extreme convolutions larger than 31x31 and test whether the performance gap can be eliminated by strategically enlarging convolutions. This study ends up with a recipe for applying extremely large kernels from the perspective of sparsity, which can smoothly scale up kernels to 61x61 with better performance. Built on this recipe, we propose Sparse Large Kernel Network (SLaK), a pure CNN architecture equipped with 51x51 kernels that can perform on par with or better than state-of-the-art hierarchical Transformers and modern ConvNet architectures like ConvNeXt and RepLKNet, on ImageNet classification as well as typical downstream tasks. Our code is available here https://github.com/VITA-Group/SLaK.

The Unreasonable Effectiveness of Random Pruning: Return of the Most Naive Baseline for Sparse Training

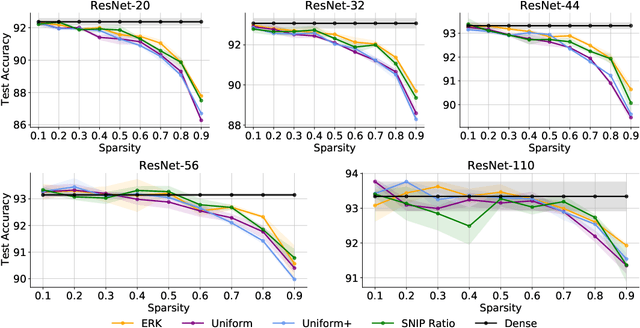
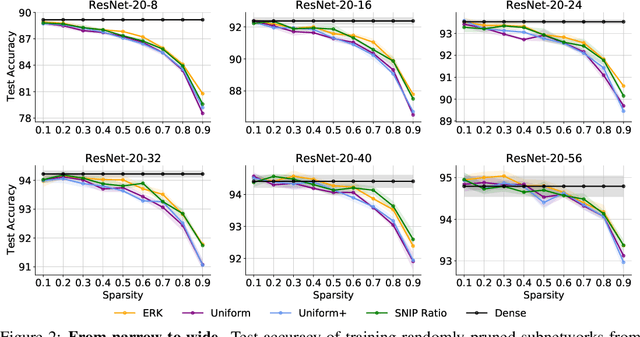
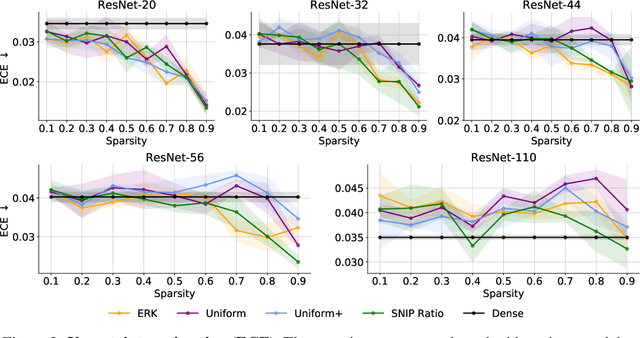
Random pruning is arguably the most naive way to attain sparsity in neural networks, but has been deemed uncompetitive by either post-training pruning or sparse training. In this paper, we focus on sparse training and highlight a perhaps counter-intuitive finding, that random pruning at initialization can be quite powerful for the sparse training of modern neural networks. Without any delicate pruning criteria or carefully pursued sparsity structures, we empirically demonstrate that sparsely training a randomly pruned network from scratch can match the performance of its dense equivalent. There are two key factors that contribute to this revival: (i) the network sizes matter: as the original dense networks grow wider and deeper, the performance of training a randomly pruned sparse network will quickly grow to matching that of its dense equivalent, even at high sparsity ratios; (ii) appropriate layer-wise sparsity ratios can be pre-chosen for sparse training, which shows to be another important performance booster. Simple as it looks, a randomly pruned subnetwork of Wide ResNet-50 can be sparsely trained to outperforming a dense Wide ResNet-50, on ImageNet. We also observed such randomly pruned networks outperform dense counterparts in other favorable aspects, such as out-of-distribution detection, uncertainty estimation, and adversarial robustness. Overall, our results strongly suggest there is larger-than-expected room for sparse training at scale, and the benefits of sparsity might be more universal beyond carefully designed pruning. Our source code can be found at https://github.com/VITA-Group/Random_Pruning.

Federated Dynamic Sparse Training: Computing Less, Communicating Less, Yet Learning Better

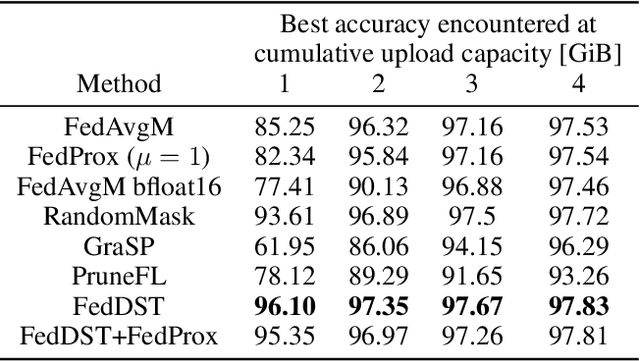
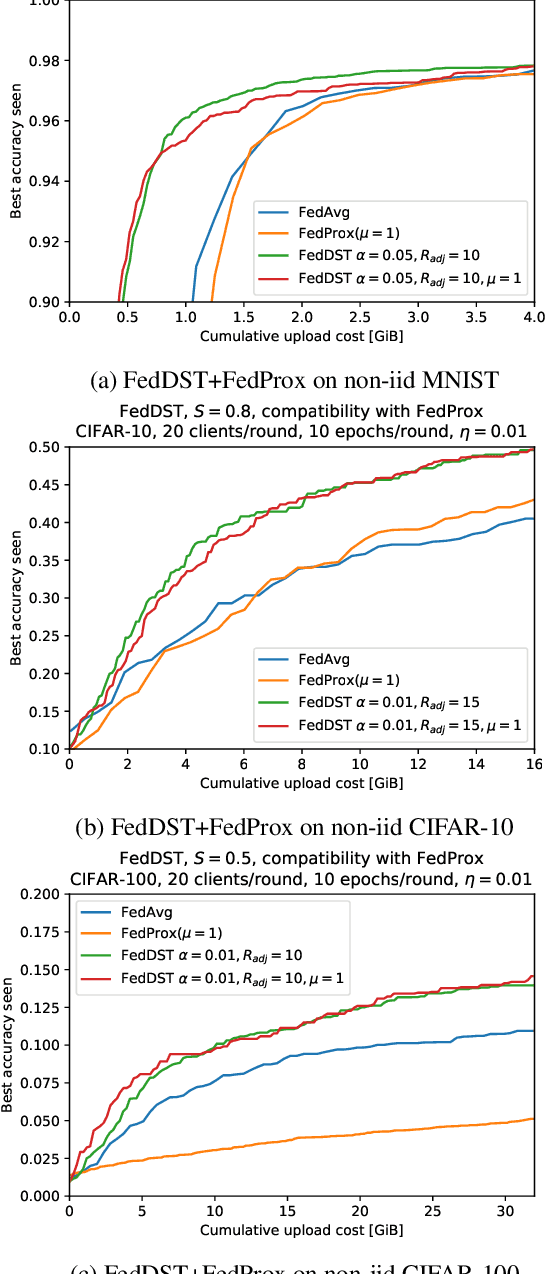
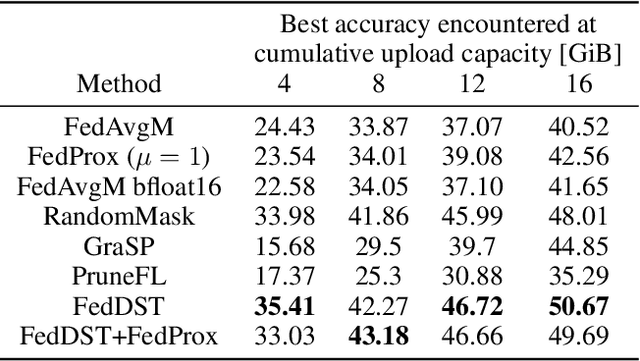
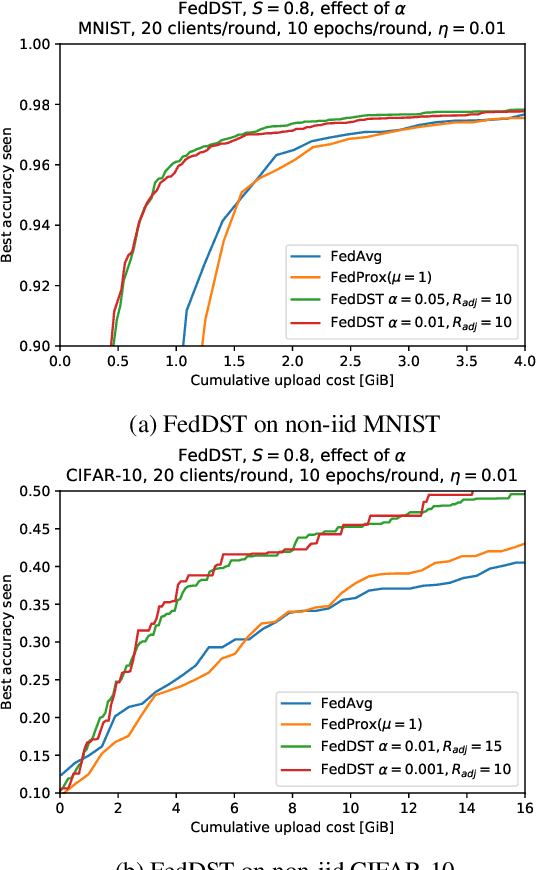
Federated learning (FL) enables distribution of machine learning workloads from the cloud to resource-limited edge devices. Unfortunately, current deep networks remain not only too compute-heavy for inference and training on edge devices, but also too large for communicating updates over bandwidth-constrained networks. In this paper, we develop, implement, and experimentally validate a novel FL framework termed Federated Dynamic Sparse Training (FedDST) by which complex neural networks can be deployed and trained with substantially improved efficiency in both on-device computation and in-network communication. At the core of FedDST is a dynamic process that extracts and trains sparse sub-networks from the target full network. With this scheme, "two birds are killed with one stone:" instead of full models, each client performs efficient training of its own sparse networks, and only sparse networks are transmitted between devices and the cloud. Furthermore, our results reveal that the dynamic sparsity during FL training more flexibly accommodates local heterogeneity in FL agents than the fixed, shared sparse masks. Moreover, dynamic sparsity naturally introduces an "in-time self-ensembling effect" into the training dynamics and improves the FL performance even over dense training. In a realistic and challenging non i.i.d. FL setting, FedDST consistently outperforms competing algorithms in our experiments: for instance, at any fixed upload data cap on non-iid CIFAR-10, it gains an impressive accuracy advantage of 10% over FedAvgM when given the same upload data cap; the accuracy gap remains 3% even when FedAvgM is given 2x the upload data cap, further demonstrating efficacy of FedDST. Code is available at: https://github.com/bibikar/feddst.

Hyperparameter Tuning is All You Need for LISTA

Learned Iterative Shrinkage-Thresholding Algorithm (LISTA) introduces the concept of unrolling an iterative algorithm and training it like a neural network. It has had great success on sparse recovery. In this paper, we show that adding momentum to intermediate variables in the LISTA network achieves a better convergence rate and, in particular, the network with instance-optimal parameters is superlinearly convergent. Moreover, our new theoretical results lead to a practical approach of automatically and adaptively calculating the parameters of a LISTA network layer based on its previous layers. Perhaps most surprisingly, such an adaptive-parameter procedure reduces the training of LISTA to tuning only three hyperparameters from data: a new record set in the context of the recent advances on trimming down LISTA complexity. We call this new ultra-light weight network HyperLISTA. Compared to state-of-the-art LISTA models, HyperLISTA achieves almost the same performance on seen data distributions and performs better when tested on unseen distributions (specifically, those with different sparsity levels and nonzero magnitudes). Code is available: https://github.com/VITA-Group/HyperLISTA.