Expressive Power of Graph Neural Networks for Quadratic Programs

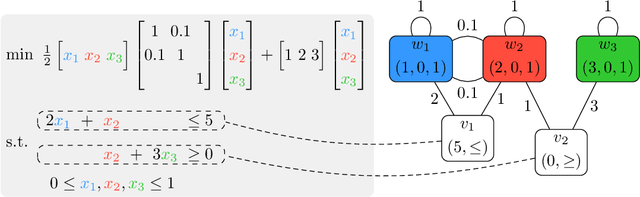
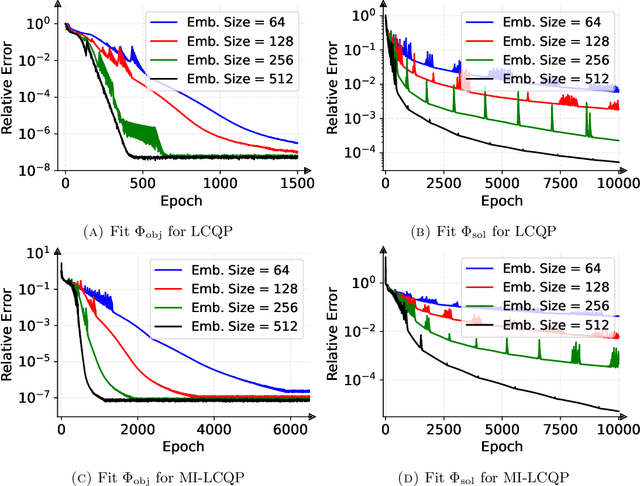
Quadratic programming (QP) is the most widely applied category of problems in nonlinear programming. Many applications require real-time/fast solutions, though not necessarily with high precision. Existing methods either involve matrix decomposition or use the preconditioned conjugate gradient method. For relatively large instances, these methods cannot achieve the real-time requirement unless there is an effective precondition. Recently, graph neural networks (GNNs) opened new possibilities for QP. Some promising empirical studies of applying GNNs for QP tasks show that GNNs can capture key characteristics of an optimization instance and provide adaptive guidance accordingly to crucial configurations during the solving process, or directly provide an approximate solution. Despite notable empirical observations, theoretical foundations are still lacking. In this work, we investigate the expressive or representative power of GNNs, a crucial aspect of neural network theory, specifically in the context of QP tasks, with both continuous and mixed-integer settings. We prove the existence of message-passing GNNs that can reliably represent key properties of quadratic programs, including feasibility, optimal objective value, and optimal solution. Our theory is validated by numerical results.