A method for improving multilingual quality and diversity of instruction fine-tuning datasets

Multilingual Instruction Fine-Tuning (IFT) is essential for enabling large language models (LLMs) to generalize effectively across diverse linguistic and cultural contexts. However, the scarcity of high-quality multilingual training data and corresponding building method remains a critical bottleneck. While data selection has shown promise in English settings, existing methods often fail to generalize across languages due to reliance on simplistic heuristics or language-specific assumptions. In this work, we introduce Multilingual Data Quality and Diversity (M-DaQ), a novel method for improving LLMs multilinguality, by selecting high-quality and semantically diverse multilingual IFT samples. We further conduct the first systematic investigation of the Superficial Alignment Hypothesis (SAH) in multilingual setting. Empirical results across 18 languages demonstrate that models fine-tuned with M-DaQ method achieve significant performance gains over vanilla baselines over 60% win rate. Human evaluations further validate these gains, highlighting the increment of cultural points in the response. We release the M-DaQ code to support future research.

RationAnomaly: Log Anomaly Detection with Rationality via Chain-of-Thought and Reinforcement Learning

Logs constitute a form of evidence signaling the operational status of software systems. Automated log anomaly detection is crucial for ensuring the reliability of modern software systems. However, existing approaches face significant limitations: traditional deep learning models lack interpretability and generalization, while methods leveraging Large Language Models are often hindered by unreliability and factual inaccuracies. To address these issues, we propose RationAnomaly, a novel framework that enhances log anomaly detection by synergizing Chain-of-Thought (CoT) fine-tuning with reinforcement learning. Our approach first instills expert-like reasoning patterns using CoT-guided supervised fine-tuning, grounded in a high-quality dataset corrected through a rigorous expert-driven process. Subsequently, a reinforcement learning phase with a multi-faceted reward function optimizes for accuracy and logical consistency, effectively mitigating hallucinations. Experimentally, RationAnomaly outperforms state-of-the-art baselines, achieving superior F1-scores on key benchmarks while providing transparent, step-by-step analytical outputs. We have released the corresponding resources, including code and datasets.

Barron Space Representations for Elliptic PDEs with Homogeneous Boundary Conditions

We study the approximation complexity of high-dimensional second-order elliptic PDEs with homogeneous boundary conditions on the unit hypercube, within the framework of Barron spaces. Under the assumption that the coefficients belong to suitably defined Barron spaces, we prove that the solution can be efficiently approximated by two-layer neural networks, circumventing the curse of dimensionality. Our results demonstrate the expressive power of shallow networks in capturing high-dimensional PDE solutions under appropriate structural assumptions.

SCFormer: Structured Channel-wise Transformer with Cumulative Historical State for Multivariate Time Series Forecasting

The Transformer model has shown strong performance in multivariate time series forecasting by leveraging channel-wise self-attention. However, this approach lacks temporal constraints when computing temporal features and does not utilize cumulative historical series effectively.To address these limitations, we propose the Structured Channel-wise Transformer with Cumulative Historical state (SCFormer). SCFormer introduces temporal constraints to all linear transformations, including the query, key, and value matrices, as well as the fully connected layers within the Transformer. Additionally, SCFormer employs High-order Polynomial Projection Operators (HiPPO) to deal with cumulative historical time series, allowing the model to incorporate information beyond the look-back window during prediction. Extensive experiments on multiple real-world datasets demonstrate that SCFormer significantly outperforms mainstream baselines, highlighting its effectiveness in enhancing time series forecasting. The code is publicly available at https://github.com/ShiweiGuo1995/SCFormer

ValuePilot: A Two-Phase Framework for Value-Driven Decision-Making

Despite recent advances in artificial intelligence (AI), it poses challenges to ensure personalized decision-making in tasks that are not considered in training datasets. To address this issue, we propose ValuePilot, a two-phase value-driven decision-making framework comprising a dataset generation toolkit DGT and a decision-making module DMM trained on the generated data. DGT is capable of generating scenarios based on value dimensions and closely mirroring real-world tasks, with automated filtering techniques and human curation to ensure the validity of the dataset. In the generated dataset, DMM learns to recognize the inherent values of scenarios, computes action feasibility and navigates the trade-offs between multiple value dimensions to make personalized decisions. Extensive experiments demonstrate that, given human value preferences, our DMM most closely aligns with human decisions, outperforming Claude-3.5-Sonnet, Gemini-2-flash, Llama-3.1-405b and GPT-4o. This research is a preliminary exploration of value-driven decision-making. We hope it will stimulate interest in value-driven decision-making and personalized decision-making within the community.

On the Expressive Power of Subgraph Graph Neural Networks for Graphs with Bounded Cycles

Graph neural networks (GNNs) have been widely used in graph-related contexts. It is known that the separation power of GNNs is equivalent to that of the Weisfeiler-Lehman (WL) test; hence, GNNs are imperfect at identifying all non-isomorphic graphs, which severely limits their expressive power. This work investigates $k$-hop subgraph GNNs that aggregate information from neighbors with distances up to $k$ and incorporate the subgraph structure. We prove that under appropriate assumptions, the $k$-hop subgraph GNNs can approximate any permutation-invariant/equivariant continuous function over graphs without cycles of length greater than $2k+1$ within any error tolerance. We also provide an extension to $k$-hop GNNs without incorporating the subgraph structure. Our numerical experiments on established benchmarks and novel architectures validate our theory on the relationship between the information aggregation distance and the cycle size.

Residual connections provably mitigate oversmoothing in graph neural networks

Graph neural networks (GNNs) have achieved remarkable empirical success in processing and representing graph-structured data across various domains. However, a significant challenge known as "oversmoothing" persists, where vertex features become nearly indistinguishable in deep GNNs, severely restricting their expressive power and practical utility. In this work, we analyze the asymptotic oversmoothing rates of deep GNNs with and without residual connections by deriving explicit convergence rates for a normalized vertex similarity measure. Our analytical framework is grounded in the multiplicative ergodic theorem. Furthermore, we demonstrate that adding residual connections effectively mitigates or prevents oversmoothing across several broad families of parameter distributions. The theoretical findings are strongly supported by numerical experiments.

LogEval: A Comprehensive Benchmark Suite for Large Language Models In Log Analysis

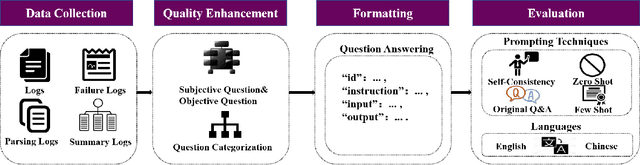
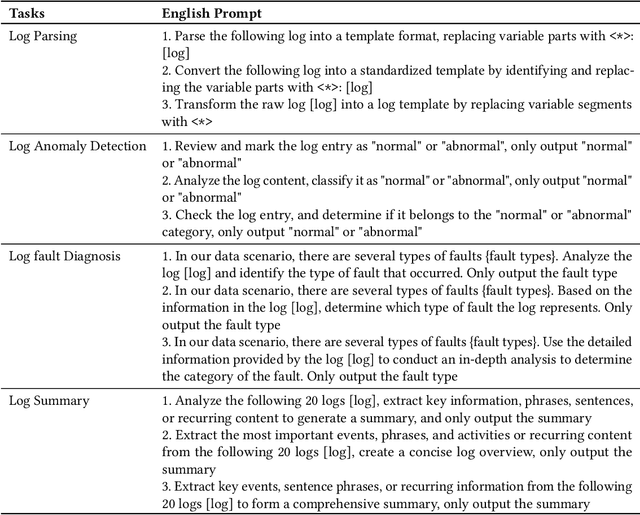
Log analysis is crucial for ensuring the orderly and stable operation of information systems, particularly in the field of Artificial Intelligence for IT Operations (AIOps). Large Language Models (LLMs) have demonstrated significant potential in natural language processing tasks. In the AIOps domain, they excel in tasks such as anomaly detection, root cause analysis of faults, operations and maintenance script generation, and alert information summarization. However, the performance of current LLMs in log analysis tasks remains inadequately validated. To address this gap, we introduce LogEval, a comprehensive benchmark suite designed to evaluate the capabilities of LLMs in various log analysis tasks for the first time. This benchmark covers tasks such as log parsing, log anomaly detection, log fault diagnosis, and log summarization. LogEval evaluates each task using 4,000 publicly available log data entries and employs 15 different prompts for each task to ensure a thorough and fair assessment. By rigorously evaluating leading LLMs, we demonstrate the impact of various LLM technologies on log analysis performance, focusing on aspects such as self-consistency and few-shot contextual learning. We also discuss findings related to model quantification, Chinese-English question-answering evaluation, and prompt engineering. These findings provide insights into the strengths and weaknesses of LLMs in multilingual environments and the effectiveness of different prompt strategies. Various evaluation methods are employed for different tasks to accurately measure the performance of LLMs in log analysis, ensuring a comprehensive assessment. The insights gained from LogEvals evaluation reveal the strengths and limitations of LLMs in log analysis tasks, providing valuable guidance for researchers and practitioners.

Expressive Power of Graph Neural Networks for Quadratic Programs

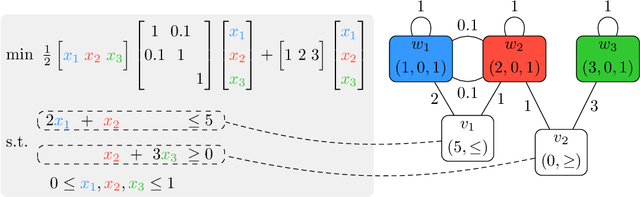
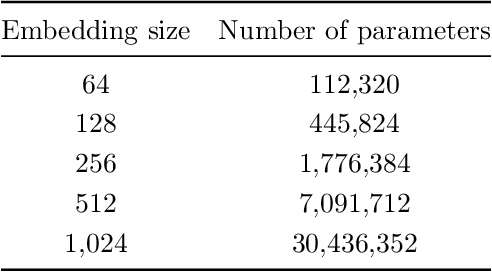
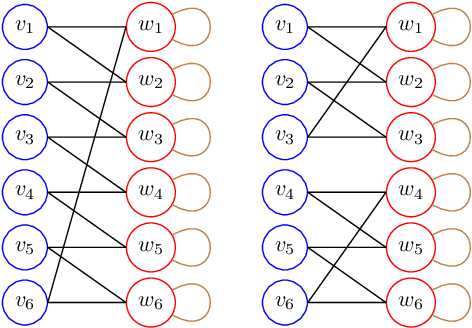
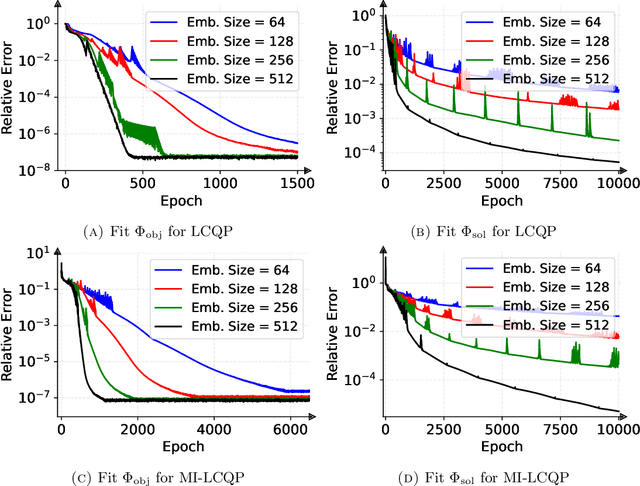
Quadratic programming (QP) is the most widely applied category of problems in nonlinear programming. Many applications require real-time/fast solutions, though not necessarily with high precision. Existing methods either involve matrix decomposition or use the preconditioned conjugate gradient method. For relatively large instances, these methods cannot achieve the real-time requirement unless there is an effective precondition. Recently, graph neural networks (GNNs) opened new possibilities for QP. Some promising empirical studies of applying GNNs for QP tasks show that GNNs can capture key characteristics of an optimization instance and provide adaptive guidance accordingly to crucial configurations during the solving process, or directly provide an approximate solution. Despite notable empirical observations, theoretical foundations are still lacking. In this work, we investigate the expressive or representative power of GNNs, a crucial aspect of neural network theory, specifically in the context of QP tasks, with both continuous and mixed-integer settings. We prove the existence of message-passing GNNs that can reliably represent key properties of quadratic programs, including feasibility, optimal objective value, and optimal solution. Our theory is validated by numerical results.

Stochastic Gradient Langevin Unlearning

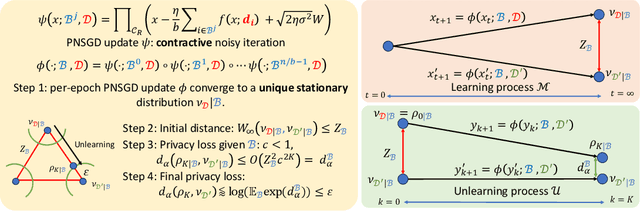
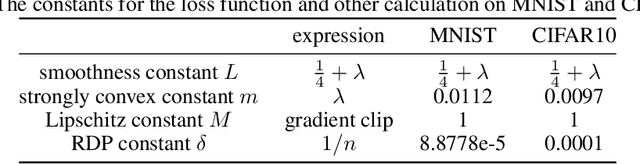
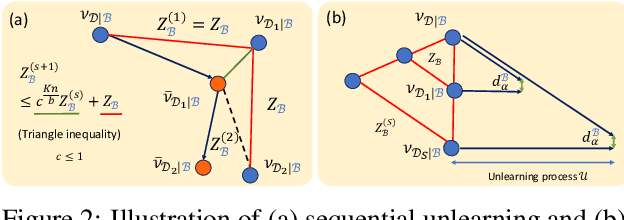
``The right to be forgotten'' ensured by laws for user data privacy becomes increasingly important. Machine unlearning aims to efficiently remove the effect of certain data points on the trained model parameters so that it can be approximately the same as if one retrains the model from scratch. This work proposes stochastic gradient Langevin unlearning, the first unlearning framework based on noisy stochastic gradient descent (SGD) with privacy guarantees for approximate unlearning problems under convexity assumption. Our results show that mini-batch gradient updates provide a superior privacy-complexity trade-off compared to the full-batch counterpart. There are numerous algorithmic benefits of our unlearning approach, including complexity saving compared to retraining, and supporting sequential and batch unlearning. To examine the privacy-utility-complexity trade-off of our method, we conduct experiments on benchmark datasets compared against prior works. Our approach achieves a similar utility under the same privacy constraint while using $2\%$ and $10\%$ of the gradient computations compared with the state-of-the-art gradient-based approximate unlearning methods for mini-batch and full-batch settings, respectively.