On the number of modes of Gaussian kernel density estimators

We consider the Gaussian kernel density estimator with bandwidth $\beta^{-\frac12}$ of $n$ iid Gaussian samples. Using the Kac-Rice formula and an Edgeworth expansion, we prove that the expected number of modes on the real line scales as $\Theta(\sqrt{\beta\log\beta})$ as $\beta,n\to\infty$ provided $n^c\lesssim \beta\lesssim n^{2-c}$ for some constant $c>0$. An impetus behind this investigation is to determine the number of clusters to which Transformers are drawn in a metastable state.

Clustering in Causal Attention Masking

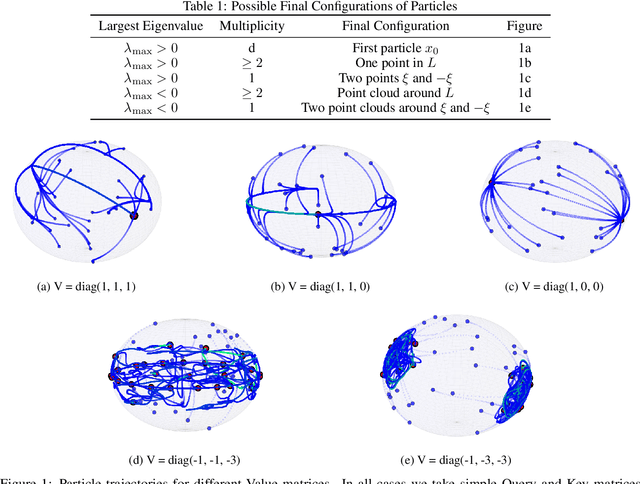
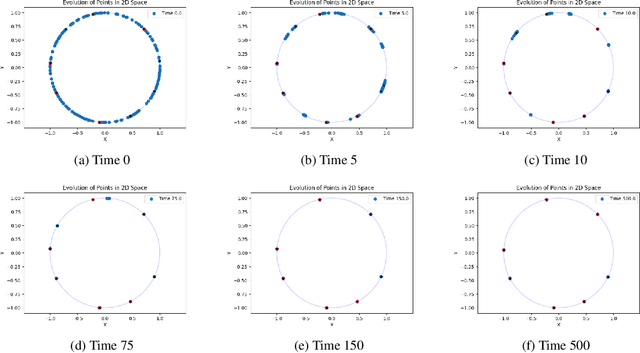
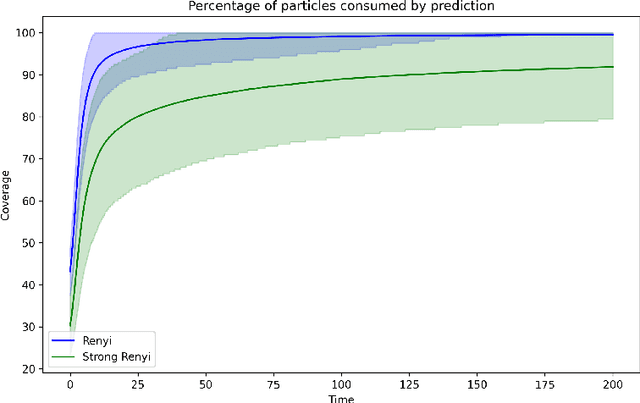
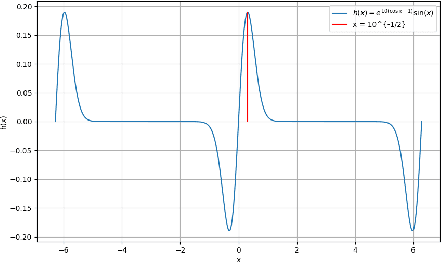
This work presents a modification of the self-attention dynamics proposed by Geshkovski et al. (arXiv:2312.10794) to better reflect the practically relevant, causally masked attention used in transformer architectures for generative AI. This modification translates into an interacting particle system that cannot be interpreted as a mean-field gradient flow. Despite this loss of structure, we significantly strengthen the results of Geshkovski et al. (arXiv:2312.10794) in this context: While previous rigorous results focused on cases where all three matrices (Key, Query, and Value) were scaled identities, we prove asymptotic convergence to a single cluster for arbitrary key-query matrices and a value matrix equal to the identity. Additionally, we establish a connection to the classical R\'enyi parking problem from combinatorial geometry to make initial theoretical steps towards demonstrating the existence of meta-stable states.

Measure-to-measure interpolation using Transformers

Transformers are deep neural network architectures that underpin the recent successes of large language models. Unlike more classical architectures that can be viewed as point-to-point maps, a Transformer acts as a measure-to-measure map implemented as specific interacting particle system on the unit sphere: the input is the empirical measure of tokens in a prompt and its evolution is governed by the continuity equation. In fact, Transformers are not limited to empirical measures and can in principle process any input measure. As the nature of data processed by Transformers is expanding rapidly, it is important to investigate their expressive power as maps from an arbitrary measure to another arbitrary measure. To that end, we provide an explicit choice of parameters that allows a single Transformer to match $N$ arbitrary input measures to $N$ arbitrary target measures, under the minimal assumption that every pair of input-target measures can be matched by some transport map.

Dynamic metastability in the self-attention model

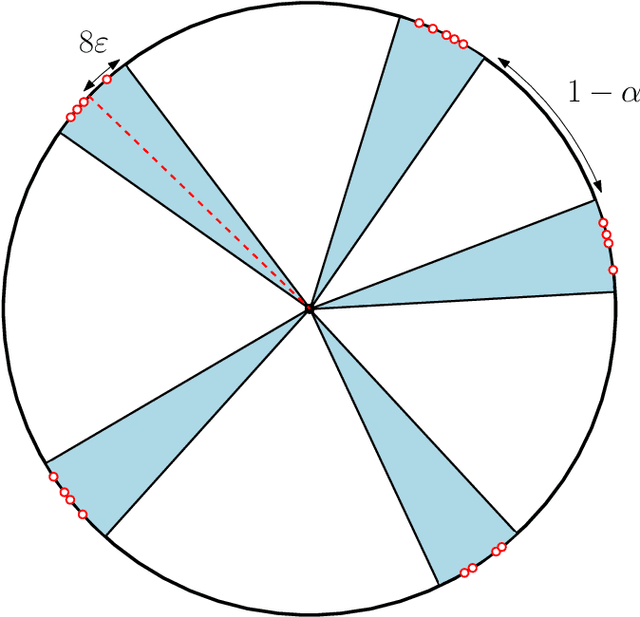
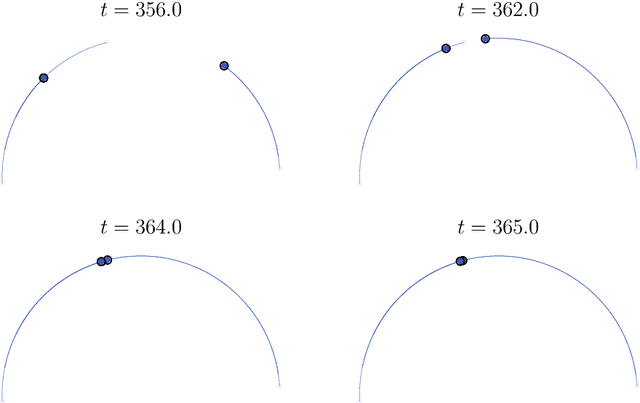
We consider the self-attention model - an interacting particle system on the unit sphere, which serves as a toy model for Transformers, the deep neural network architecture behind the recent successes of large language models. We prove the appearance of dynamic metastability conjectured in [GLPR23] - although particles collapse to a single cluster in infinite time, they remain trapped near a configuration of several clusters for an exponentially long period of time. By leveraging a gradient flow interpretation of the system, we also connect our result to an overarching framework of slow motion of gradient flows proposed by Otto and Reznikoff [OR07] in the context of coarsening and the Allen-Cahn equation. We finally probe the dynamics beyond the exponentially long period of metastability, and illustrate that, under an appropriate time-rescaling, the energy reaches its global maximum in finite time and has a staircase profile, with trajectories manifesting saddle-to-saddle-like behavior, reminiscent of recent works in the analysis of training dynamics via gradient descent for two-layer neural networks.

Statistical optimal transport

We present an introduction to the field of statistical optimal transport, based on lectures given at \'Ecole d'\'Et\'e de Probabilit\'es de Saint-Flour XLIX.

A mathematical perspective on Transformers

Transformers play a central role in the inner workings of large language models. We develop a mathematical framework for analyzing Transformers based on their interpretation as interacting particle systems, which reveals that clusters emerge in long time. Our study explores the underlying theory and offers new perspectives for mathematicians as well as computer scientists.

Covariance alignment: from maximum likelihood estimation to Gromov-Wasserstein

Feature alignment methods are used in many scientific disciplines for data pooling, annotation, and comparison. As an instance of a permutation learning problem, feature alignment presents significant statistical and computational challenges. In this work, we propose the covariance alignment model to study and compare various alignment methods and establish a minimax lower bound for covariance alignment that has a non-standard dimension scaling because of the presence of a nuisance parameter. This lower bound is in fact minimax optimal and is achieved by a natural quasi MLE. However, this estimator involves a search over all permutations which is computationally infeasible even when the problem has moderate size. To overcome this limitation, we show that the celebrated Gromov-Wasserstein algorithm from optimal transport which is more amenable to fast implementation even on large-scale problems is also minimax optimal. These results give the first statistical justification for the deployment of the Gromov-Wasserstein algorithm in practice.

Optimal transport for automatic alignment of untargeted metabolomic data

Untargeted metabolomic profiling through liquid chromatography-mass spectrometry (LC-MS) measures a vast array of metabolites within biospecimens, advancing drug development, disease diagnosis, and risk prediction. However, the low throughput of LC-MS poses a major challenge for biomarker discovery, annotation, and experimental comparison, necessitating the merging of multiple datasets. Current data pooling methods encounter practical limitations due to their vulnerability to data variations and hyperparameter dependence. Here we introduce GromovMatcher, a flexible and user-friendly algorithm that automatically combines LC-MS datasets using optimal transport. By capitalizing on feature intensity correlation structures, GromovMatcher delivers superior alignment accuracy and robustness compared to existing approaches. This algorithm scales to thousands of features requiring minimal hyperparameter tuning. Applying our method to experimental patient studies of liver and pancreatic cancer, we discover shared metabolic features related to patient alcohol intake, demonstrating how GromovMatcher facilitates the search for biomarkers associated with lifestyle risk factors linked to several cancer types.

The emergence of clusters in self-attention dynamics

Viewing Transformers as interacting particle systems, we describe the geometry of learned representations when the weights are not time dependent. We show that particles, representing tokens, tend to cluster toward particular limiting objects as time tends to infinity. Cluster locations are determined by the initial tokens, confirming context-awareness of representations learned by Transformers. Using techniques from dynamical systems and partial differential equations, we show that the type of limiting object that emerges depends on the spectrum of the value matrix. Additionally, in the one-dimensional case we prove that the self-attention matrix converges to a low-rank Boolean matrix. The combination of these results mathematically confirms the empirical observation made by Vaswani et al. [VSP'17] that leaders appear in a sequence of tokens when processed by Transformers.

Learning Gaussian Mixtures Using the Wasserstein-Fisher-Rao Gradient Flow

Gaussian mixture models form a flexible and expressive parametric family of distributions that has found applications in a wide variety of applications. Unfortunately, fitting these models to data is a notoriously hard problem from a computational perspective. Currently, only moment-based methods enjoy theoretical guarantees while likelihood-based methods are dominated by heuristics such as Expectation-Maximization that are known to fail in simple examples. In this work, we propose a new algorithm to compute the nonparametric maximum likelihood estimator (NPMLE) in a Gaussian mixture model. Our method is based on gradient descent over the space of probability measures equipped with the Wasserstein-Fisher-Rao geometry for which we establish convergence guarantees. In practice, it can be approximated using an interacting particle system where the weight and location of particles are updated alternately. We conduct extensive numerical experiments to confirm the effectiveness of the proposed algorithm compared not only to classical benchmarks but also to similar gradient descent algorithms with respect to simpler geometries. In particular, these simulations illustrate the benefit of updating both weight and location of the interacting particles.