Fast Convergence for High-Order ODE Solvers in Diffusion Probabilistic Models

Diffusion probabilistic models generate samples by learning to reverse a noise-injection process that transforms data into noise. Reformulating this reverse process as a deterministic probability flow ordinary differential equation (ODE) enables efficient sampling using high-order solvers, often requiring only $\mathcal{O}(10)$ steps. Since the score function is typically approximated by a neural network, analyzing the interaction between its regularity, approximation error, and numerical integration error is key to understanding the overall sampling accuracy. In this work, we continue our analysis of the convergence properties of the deterministic sampling methods derived from probability flow ODEs [25], focusing on $p$-th order (exponential) Runge-Kutta schemes for any integer $p \geq 1$. Under the assumption that the first and second derivatives of the approximate score function are bounded, we develop $p$-th order (exponential) Runge-Kutta schemes and demonstrate that the total variation distance between the target distribution and the generated data distribution can be bounded above by \begin{align*} O\bigl(d^{\frac{7}{4}}\varepsilon_{\text{score}}^{\frac{1}{2}} +d(dH_{\max})^p\bigr), \end{align*} where $\varepsilon^2_{\text{score}}$ denotes the $L^2$ error in the score function approximation, $d$ is the data dimension and $H_{\max}$ represents the maximum step size used in the solver. We numerically verify the regularity assumption on benchmark datasets, confirming that the first and second derivatives of the approximate score function remain bounded in practice. Our theoretical guarantees hold for general forward processes with arbitrary variance schedules.

Quantitative Clustering in Mean-Field Transformer Models

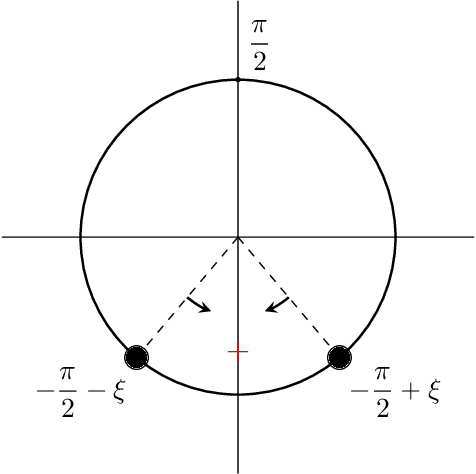
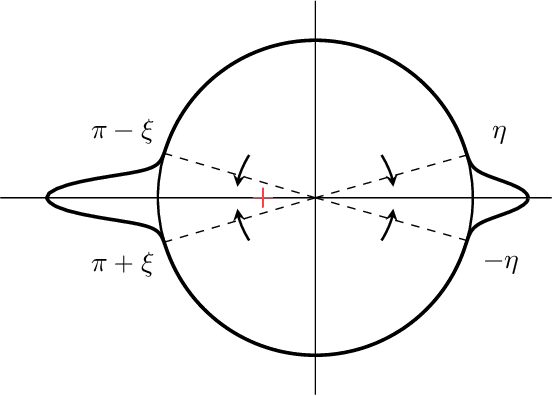
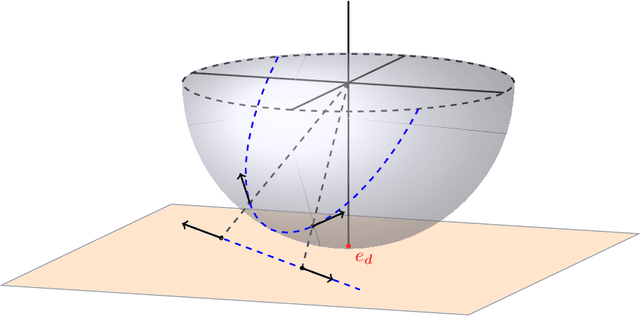
The evolution of tokens through a deep transformer models can be modeled as an interacting particle system that has been shown to exhibit an asymptotic clustering behavior akin to the synchronization phenomenon in Kuramoto models. In this work, we investigate the long-time clustering of mean-field transformer models. More precisely, we establish exponential rates of contraction to a Dirac point mass for any suitably regular initialization under some assumptions on the parameters of transformer models, any suitably regular mean-field initialization synchronizes exponentially fast with some quantitative rates.

Residual connections provably mitigate oversmoothing in graph neural networks

Graph neural networks (GNNs) have achieved remarkable empirical success in processing and representing graph-structured data across various domains. However, a significant challenge known as "oversmoothing" persists, where vertex features become nearly indistinguishable in deep GNNs, severely restricting their expressive power and practical utility. In this work, we analyze the asymptotic oversmoothing rates of deep GNNs with and without residual connections by deriving explicit convergence rates for a normalized vertex similarity measure. Our analytical framework is grounded in the multiplicative ergodic theorem. Furthermore, we demonstrate that adding residual connections effectively mitigates or prevents oversmoothing across several broad families of parameter distributions. The theoretical findings are strongly supported by numerical experiments.

Convergence Analysis of Probability Flow ODE for Score-based Generative Models

Score-based generative models have emerged as a powerful approach for sampling high-dimensional probability distributions. Despite their effectiveness, their theoretical underpinnings remain relatively underdeveloped. In this work, we study the convergence properties of deterministic samplers based on probability flow ODEs from both theoretical and numerical perspectives. Assuming access to $L^2$-accurate estimates of the score function, we prove the total variation between the target and the generated data distributions can be bounded above by $\mathcal{O}(d\sqrt{\delta})$ in the continuous time level, where $d$ denotes the data dimension and $\delta$ represents the $L^2$-score matching error. For practical implementations using a $p$-th order Runge-Kutta integrator with step size $h$, we establish error bounds of $\mathcal{O}(d(\sqrt{\delta} + (dh)^p))$ at the discrete level. Finally, we present numerical studies on problems up to $128$ dimensions to verify our theory, which indicate a better score matching error and dimension dependence.