Fisher-Rao Gradient Flow: Geodesic Convexity and Functional Inequalities

The dynamics of probability density functions has been extensively studied in science and engineering to understand physical phenomena and facilitate algorithmic design. Of particular interest are dynamics that can be formulated as gradient flows of energy functionals under the Wasserstein metric. The development of functional inequalities, such as the log-Sobolev inequality, plays a pivotal role in analyzing the convergence of these dynamics. The goal of this paper is to parallel the success of techniques using functional inequalities, for dynamics that are gradient flows under the Fisher-Rao metric, with various $f$-divergences as energy functionals. Such dynamics take the form of a nonlocal differential equation, for which existing analysis critically relies on using the explicit solution formula in special cases. We provide a comprehensive study on functional inequalities and the relevant geodesic convexity for Fisher-Rao gradient flows under minimal assumptions. A notable feature of the obtained functional inequalities is that they do not depend on the log-concavity or log-Sobolev constants of the target distribution. Consequently, the convergence rate of the dynamics (assuming well-posed) is uniform across general target distributions, making them potentially desirable dynamics for posterior sampling applications in Bayesian inference.

Efficient, Multimodal, and Derivative-Free Bayesian Inference With Fisher-Rao Gradient Flows

In this paper, we study efficient approximate sampling for probability distributions known up to normalization constants. We specifically focus on a problem class arising in Bayesian inference for large-scale inverse problems in science and engineering applications. The computational challenges we address with the proposed methodology are: (i) the need for repeated evaluations of expensive forward models; (ii) the potential existence of multiple modes; and (iii) the fact that gradient of, or adjoint solver for, the forward model might not be feasible. While existing Bayesian inference methods meet some of these challenges individually, we propose a framework that tackles all three systematically. Our approach builds upon the Fisher-Rao gradient flow in probability space, yielding a dynamical system for probability densities that converges towards the target distribution at a uniform exponential rate. This rapid convergence is advantageous for the computational burden outlined in (i). We apply Gaussian mixture approximations with operator splitting techniques to simulate the flow numerically; the resulting approximation can capture multiple modes thus addressing (ii). Furthermore, we employ the Kalman methodology to facilitate a derivative-free update of these Gaussian components and their respective weights, addressing the issue in (iii). The proposed methodology results in an efficient derivative-free sampler flexible enough to handle multi-modal distributions: Gaussian Mixture Kalman Inversion (GMKI). The effectiveness of GMKI is demonstrated both theoretically and numerically in several experiments with multimodal target distributions, including proof-of-concept and two-dimensional examples, as well as a large-scale application: recovering the Navier-Stokes initial condition from solution data at positive times.

Convergence Analysis of Probability Flow ODE for Score-based Generative Models

Score-based generative models have emerged as a powerful approach for sampling high-dimensional probability distributions. Despite their effectiveness, their theoretical underpinnings remain relatively underdeveloped. In this work, we study the convergence properties of deterministic samplers based on probability flow ODEs from both theoretical and numerical perspectives. Assuming access to $L^2$-accurate estimates of the score function, we prove the total variation between the target and the generated data distributions can be bounded above by $\mathcal{O}(d\sqrt{\delta})$ in the continuous time level, where $d$ denotes the data dimension and $\delta$ represents the $L^2$-score matching error. For practical implementations using a $p$-th order Runge-Kutta integrator with step size $h$, we establish error bounds of $\mathcal{O}(d(\sqrt{\delta} + (dh)^p))$ at the discrete level. Finally, we present numerical studies on problems up to $128$ dimensions to verify our theory, which indicate a better score matching error and dimension dependence.

An operator learning perspective on parameter-to-observable maps

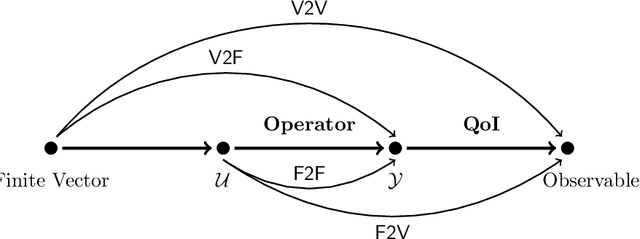
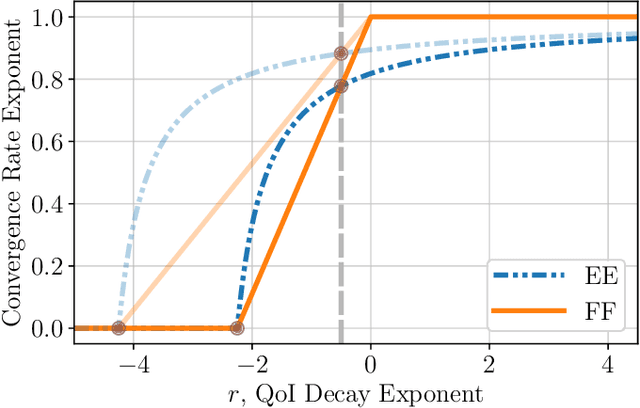
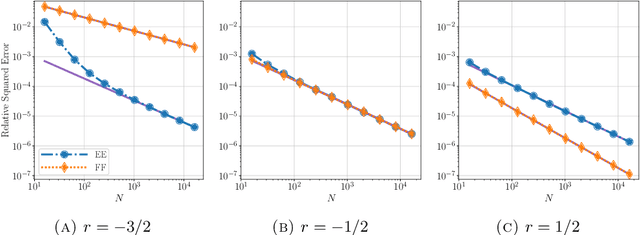
Computationally efficient surrogates for parametrized physical models play a crucial role in science and engineering. Operator learning provides data-driven surrogates that map between function spaces. However, instead of full-field measurements, often the available data are only finite-dimensional parametrizations of model inputs or finite observables of model outputs. Building off of Fourier Neural Operators, this paper introduces the Fourier Neural Mappings (FNMs) framework that is able to accommodate such finite-dimensional inputs and outputs. The paper develops universal approximation theorems for the method. Moreover, in many applications the underlying parameter-to-observable (PtO) map is defined implicitly through an infinite-dimensional operator, such as the solution operator of a partial differential equation. A natural question is whether it is more data-efficient to learn the PtO map end-to-end or first learn the solution operator and subsequently compute the observable from the full-field solution. A theoretical analysis of Bayesian nonparametric regression of linear functionals, which is of independent interest, suggests that the end-to-end approach can actually have worse sample complexity. Extending beyond the theory, numerical results for the FNM approximation of three nonlinear PtO maps demonstrate the benefits of the operator learning perspective that this paper adopts.

Sampling via Gradient Flows in the Space of Probability Measures

Sampling a target probability distribution with an unknown normalization constant is a fundamental challenge in computational science and engineering. Recent work shows that algorithms derived by considering gradient flows in the space of probability measures open up new avenues for algorithm development. This paper makes three contributions to this sampling approach by scrutinizing the design components of such gradient flows. Any instantiation of a gradient flow for sampling needs an energy functional and a metric to determine the flow, as well as numerical approximations of the flow to derive algorithms. Our first contribution is to show that the Kullback-Leibler divergence, as an energy functional, has the unique property (among all f-divergences) that gradient flows resulting from it do not depend on the normalization constant of the target distribution. Our second contribution is to study the choice of metric from the perspective of invariance. The Fisher-Rao metric is known as the unique choice (up to scaling) that is diffeomorphism invariant. As a computationally tractable alternative, we introduce a relaxed, affine invariance property for the metrics and gradient flows. In particular, we construct various affine invariant Wasserstein and Stein gradient flows. Affine invariant gradient flows are shown to behave more favorably than their non-affine-invariant counterparts when sampling highly anisotropic distributions, in theory and by using particle methods. Our third contribution is to study, and develop efficient algorithms based on Gaussian approximations of the gradient flows; this leads to an alternative to particle methods. We establish connections between various Gaussian approximate gradient flows, discuss their relation to gradient methods arising from parametric variational inference, and study their convergence properties both theoretically and numerically.

Gradient Flows for Sampling: Mean-Field Models, Gaussian Approximations and Affine Invariance

Sampling a probability distribution with an unknown normalization constant is a fundamental problem in computational science and engineering. This task may be cast as an optimization problem over all probability measures, and an initial distribution can be evolved to the desired minimizer dynamically via gradient flows. Mean-field models, whose law is governed by the gradient flow in the space of probability measures, may also be identified; particle approximations of these mean-field models form the basis of algorithms. The gradient flow approach is also the basis of algorithms for variational inference, in which the optimization is performed over a parameterized family of probability distributions such as Gaussians, and the underlying gradient flow is restricted to the parameterized family. By choosing different energy functionals and metrics for the gradient flow, different algorithms with different convergence properties arise. In this paper, we concentrate on the Kullback-Leibler divergence after showing that, up to scaling, it has the unique property that the gradient flows resulting from this choice of energy do not depend on the normalization constant. For the metrics, we focus on variants of the Fisher-Rao, Wasserstein, and Stein metrics; we introduce the affine invariance property for gradient flows, and their corresponding mean-field models, determine whether a given metric leads to affine invariance, and modify it to make it affine invariant if it does not. We study the resulting gradient flows in both probability density space and Gaussian space. The flow in the Gaussian space may be understood as a Gaussian approximation of the flow. We demonstrate that the Gaussian approximation based on the metric and through moment closure coincide, establish connections between them, and study their long-time convergence properties showing the advantages of affine invariance.

Bayesian Spline Learning for Equation Discovery of Nonlinear Dynamics with Quantified Uncertainty

Nonlinear dynamics are ubiquitous in science and engineering applications, but the physics of most complex systems is far from being fully understood. Discovering interpretable governing equations from measurement data can help us understand and predict the behavior of complex dynamic systems. Although extensive work has recently been done in this field, robustly distilling explicit model forms from very sparse data with considerable noise remains intractable. Moreover, quantifying and propagating the uncertainty of the identified system from noisy data is challenging, and relevant literature is still limited. To bridge this gap, we develop a novel Bayesian spline learning framework to identify parsimonious governing equations of nonlinear (spatio)temporal dynamics from sparse, noisy data with quantified uncertainty. The proposed method utilizes spline basis to handle the data scarcity and measurement noise, upon which a group of derivatives can be accurately computed to form a library of candidate model terms. The equation residuals are used to inform the spline learning in a Bayesian manner, where approximate Bayesian uncertainty calibration techniques are employed to approximate posterior distributions of the trainable parameters. To promote the sparsity, an iterative sequential-threshold Bayesian learning approach is developed, using the alternative direction optimization strategy to systematically approximate L0 sparsity constraints. The proposed algorithm is evaluated on multiple nonlinear dynamical systems governed by canonical ordinary and partial differential equations, and the merit/superiority of the proposed method is demonstrated by comparison with state-of-the-art methods.

Fourier Neural Operator with Learned Deformations for PDEs on General Geometries

Deep learning surrogate models have shown promise in solving partial differential equations (PDEs). Among them, the Fourier neural operator (FNO) achieves good accuracy, and is significantly faster compared to numerical solvers, on a variety of PDEs, such as fluid flows. However, the FNO uses the Fast Fourier transform (FFT), which is limited to rectangular domains with uniform grids. In this work, we propose a new framework, viz., geo-FNO, to solve PDEs on arbitrary geometries. Geo-FNO learns to deform the input (physical) domain, which may be irregular, into a latent space with a uniform grid. The FNO model with the FFT is applied in the latent space. The resulting geo-FNO model has both the computation efficiency of FFT and the flexibility of handling arbitrary geometries. Our geo-FNO is also flexible in terms of its input formats, viz., point clouds, meshes, and design parameters are all valid inputs. We consider a variety of PDEs such as the Elasticity, Plasticity, Euler's, and Navier-Stokes equations, and both forward modeling and inverse design problems. Geo-FNO is $10^5$ times faster than the standard numerical solvers and twice more accurate compared to direct interpolation on existing ML-based PDE solvers such as the standard FNO.

Long Random Matrices and Tensor Unfolding

In this paper, we consider the singular values and singular vectors of low rank perturbations of large rectangular random matrices, in the regime the matrix is "long": we allow the number of rows (columns) to grow polynomially in the number of columns (rows). We prove there exists a critical signal-to-noise ratio (depending on the dimensions of the matrix), and the extreme singular values and singular vectors exhibit a BBP type phase transition. As a main application, we investigate the tensor unfolding algorithm for the asymmetric rank-one spiked tensor model, and obtain an exact threshold, which is independent of the procedure of tensor unfolding. If the signal-to-noise ratio is above the threshold, tensor unfolding detects the signals; otherwise, it fails to capture the signals.