Fisher-Rao Gradient Flow: Geodesic Convexity and Functional Inequalities

The dynamics of probability density functions has been extensively studied in science and engineering to understand physical phenomena and facilitate algorithmic design. Of particular interest are dynamics that can be formulated as gradient flows of energy functionals under the Wasserstein metric. The development of functional inequalities, such as the log-Sobolev inequality, plays a pivotal role in analyzing the convergence of these dynamics. The goal of this paper is to parallel the success of techniques using functional inequalities, for dynamics that are gradient flows under the Fisher-Rao metric, with various $f$-divergences as energy functionals. Such dynamics take the form of a nonlocal differential equation, for which existing analysis critically relies on using the explicit solution formula in special cases. We provide a comprehensive study on functional inequalities and the relevant geodesic convexity for Fisher-Rao gradient flows under minimal assumptions. A notable feature of the obtained functional inequalities is that they do not depend on the log-concavity or log-Sobolev constants of the target distribution. Consequently, the convergence rate of the dynamics (assuming well-posed) is uniform across general target distributions, making them potentially desirable dynamics for posterior sampling applications in Bayesian inference.

Enhancement of damaged-image prediction through Cahn-Hilliard Image Inpainting

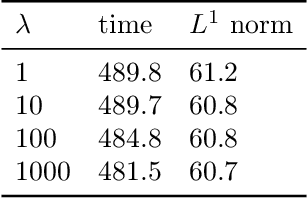
We assess the benefit of including an image inpainting filter before passing damaged images into a classification neural network. For this we employ a modified Cahn-Hilliard equation as an image inpainting filter, which is solved via a finite volume scheme with reduced computational cost and adequate properties for energy stability and boundedness. The benchmark dataset employed here is the MNIST dataset, which consists in binary images of digits. We train a neural network based of dense layers with the training set of MNIST, and subsequently we contaminate the test set with damage of different types and intensities. We then compare the prediction accuracy of the neural network with and without applying the Cahn-Hilliard filter to the damaged images test. Our results quantify the significant improvement of damaged-image prediction due to applying the Cahn-Hilliard filter, which for specific damages can increase up to 50% and is in general advantageous for low to moderate damage.