Local geometry of high-dimensional mixture models: Effective spectral theory and dynamical transitions

We study the local geometry of empirical risks in high dimensions via the spectral theory of their Hessian and information matrices. We focus on settings where the data, $(Y_\ell)_{\ell =1}^n\in \mathbb R^d$, are i.i.d. draws of a $k$-component Gaussian mixture model, and the loss depends on the projection of the data into a fixed number of vectors, namely $\mathbf{x}^\top Y$, where $\mathbf{x}\in \mathbb{R}^{d\times C}$ are the parameters, and $C$ need not equal $k$. This setting captures a broad class of problems such as classification by one and two-layer networks and regression on multi-index models. We prove exact formulas for the limits of the empirical spectral distribution and outlier eigenvalues and eigenvectors of such matrices in the proportional asymptotics limit, where the number of samples and dimension $n,d\to\infty$ and $n/d=\phi \in (0,\infty)$. These limits depend on the parameters $\mathbf{x}$ only through the summary statistic of the $(C+k)\times (C+k)$ Gram matrix of the parameters and class means, $\mathbf{G} = (\mathbf{x},\mathbf{\mu})^\top(\mathbf{x},\mathbf{\mu})$. It is known that under general conditions, when $\mathbf{x}$ is trained by stochastic gradient descent, the evolution of these same summary statistics along training converges to the solution of an autonomous system of ODEs, called the effective dynamics. This enables us to connect the spectral theory to the training dynamics. We demonstrate our general results by analyzing the effective spectrum along the effective dynamics in the case of multi-class logistic regression. In this setting, the empirical Hessian and information matrices have substantially different spectra, each with their own static and even dynamical spectral transitions.

Fisher-Rao Gradient Flow: Geodesic Convexity and Functional Inequalities

The dynamics of probability density functions has been extensively studied in science and engineering to understand physical phenomena and facilitate algorithmic design. Of particular interest are dynamics that can be formulated as gradient flows of energy functionals under the Wasserstein metric. The development of functional inequalities, such as the log-Sobolev inequality, plays a pivotal role in analyzing the convergence of these dynamics. The goal of this paper is to parallel the success of techniques using functional inequalities, for dynamics that are gradient flows under the Fisher-Rao metric, with various $f$-divergences as energy functionals. Such dynamics take the form of a nonlocal differential equation, for which existing analysis critically relies on using the explicit solution formula in special cases. We provide a comprehensive study on functional inequalities and the relevant geodesic convexity for Fisher-Rao gradient flows under minimal assumptions. A notable feature of the obtained functional inequalities is that they do not depend on the log-concavity or log-Sobolev constants of the target distribution. Consequently, the convergence rate of the dynamics (assuming well-posed) is uniform across general target distributions, making them potentially desirable dynamics for posterior sampling applications in Bayesian inference.

Efficient, Multimodal, and Derivative-Free Bayesian Inference With Fisher-Rao Gradient Flows

In this paper, we study efficient approximate sampling for probability distributions known up to normalization constants. We specifically focus on a problem class arising in Bayesian inference for large-scale inverse problems in science and engineering applications. The computational challenges we address with the proposed methodology are: (i) the need for repeated evaluations of expensive forward models; (ii) the potential existence of multiple modes; and (iii) the fact that gradient of, or adjoint solver for, the forward model might not be feasible. While existing Bayesian inference methods meet some of these challenges individually, we propose a framework that tackles all three systematically. Our approach builds upon the Fisher-Rao gradient flow in probability space, yielding a dynamical system for probability densities that converges towards the target distribution at a uniform exponential rate. This rapid convergence is advantageous for the computational burden outlined in (i). We apply Gaussian mixture approximations with operator splitting techniques to simulate the flow numerically; the resulting approximation can capture multiple modes thus addressing (ii). Furthermore, we employ the Kalman methodology to facilitate a derivative-free update of these Gaussian components and their respective weights, addressing the issue in (iii). The proposed methodology results in an efficient derivative-free sampler flexible enough to handle multi-modal distributions: Gaussian Mixture Kalman Inversion (GMKI). The effectiveness of GMKI is demonstrated both theoretically and numerically in several experiments with multimodal target distributions, including proof-of-concept and two-dimensional examples, as well as a large-scale application: recovering the Navier-Stokes initial condition from solution data at positive times.

Convergence Analysis of Probability Flow ODE for Score-based Generative Models

Score-based generative models have emerged as a powerful approach for sampling high-dimensional probability distributions. Despite their effectiveness, their theoretical underpinnings remain relatively underdeveloped. In this work, we study the convergence properties of deterministic samplers based on probability flow ODEs from both theoretical and numerical perspectives. Assuming access to $L^2$-accurate estimates of the score function, we prove the total variation between the target and the generated data distributions can be bounded above by $\mathcal{O}(d\sqrt{\delta})$ in the continuous time level, where $d$ denotes the data dimension and $\delta$ represents the $L^2$-score matching error. For practical implementations using a $p$-th order Runge-Kutta integrator with step size $h$, we establish error bounds of $\mathcal{O}(d(\sqrt{\delta} + (dh)^p))$ at the discrete level. Finally, we present numerical studies on problems up to $128$ dimensions to verify our theory, which indicate a better score matching error and dimension dependence.

Sampling via Gradient Flows in the Space of Probability Measures

Sampling a target probability distribution with an unknown normalization constant is a fundamental challenge in computational science and engineering. Recent work shows that algorithms derived by considering gradient flows in the space of probability measures open up new avenues for algorithm development. This paper makes three contributions to this sampling approach by scrutinizing the design components of such gradient flows. Any instantiation of a gradient flow for sampling needs an energy functional and a metric to determine the flow, as well as numerical approximations of the flow to derive algorithms. Our first contribution is to show that the Kullback-Leibler divergence, as an energy functional, has the unique property (among all f-divergences) that gradient flows resulting from it do not depend on the normalization constant of the target distribution. Our second contribution is to study the choice of metric from the perspective of invariance. The Fisher-Rao metric is known as the unique choice (up to scaling) that is diffeomorphism invariant. As a computationally tractable alternative, we introduce a relaxed, affine invariance property for the metrics and gradient flows. In particular, we construct various affine invariant Wasserstein and Stein gradient flows. Affine invariant gradient flows are shown to behave more favorably than their non-affine-invariant counterparts when sampling highly anisotropic distributions, in theory and by using particle methods. Our third contribution is to study, and develop efficient algorithms based on Gaussian approximations of the gradient flows; this leads to an alternative to particle methods. We establish connections between various Gaussian approximate gradient flows, discuss their relation to gradient methods arising from parametric variational inference, and study their convergence properties both theoretically and numerically.

High-dimensional SGD aligns with emerging outlier eigenspaces

We rigorously study the joint evolution of training dynamics via stochastic gradient descent (SGD) and the spectra of empirical Hessian and gradient matrices. We prove that in two canonical classification tasks for multi-class high-dimensional mixtures and either 1 or 2-layer neural networks, the SGD trajectory rapidly aligns with emerging low-rank outlier eigenspaces of the Hessian and gradient matrices. Moreover, in multi-layer settings this alignment occurs per layer, with the final layer's outlier eigenspace evolving over the course of training, and exhibiting rank deficiency when the SGD converges to sub-optimal classifiers. This establishes some of the rich predictions that have arisen from extensive numerical studies in the last decade about the spectra of Hessian and information matrices over the course of training in overparametrized networks.

How Does Information Bottleneck Help Deep Learning?

Numerous deep learning algorithms have been inspired by and understood via the notion of information bottleneck, where unnecessary information is (often implicitly) minimized while task-relevant information is maximized. However, a rigorous argument for justifying why it is desirable to control information bottlenecks has been elusive. In this paper, we provide the first rigorous learning theory for justifying the benefit of information bottleneck in deep learning by mathematically relating information bottleneck to generalization errors. Our theory proves that controlling information bottleneck is one way to control generalization errors in deep learning, although it is not the only or necessary way. We investigate the merit of our new mathematical findings with experiments across a range of architectures and learning settings. In many cases, generalization errors are shown to correlate with the degree of information bottleneck: i.e., the amount of the unnecessary information at hidden layers. This paper provides a theoretical foundation for current and future methods through the lens of information bottleneck. Our new generalization bounds scale with the degree of information bottleneck, unlike the previous bounds that scale with the number of parameters, VC dimension, Rademacher complexity, stability or robustness. Our code is publicly available at: https://github.com/xu-ji/information-bottleneck

Gradient Flows for Sampling: Mean-Field Models, Gaussian Approximations and Affine Invariance

Sampling a probability distribution with an unknown normalization constant is a fundamental problem in computational science and engineering. This task may be cast as an optimization problem over all probability measures, and an initial distribution can be evolved to the desired minimizer dynamically via gradient flows. Mean-field models, whose law is governed by the gradient flow in the space of probability measures, may also be identified; particle approximations of these mean-field models form the basis of algorithms. The gradient flow approach is also the basis of algorithms for variational inference, in which the optimization is performed over a parameterized family of probability distributions such as Gaussians, and the underlying gradient flow is restricted to the parameterized family. By choosing different energy functionals and metrics for the gradient flow, different algorithms with different convergence properties arise. In this paper, we concentrate on the Kullback-Leibler divergence after showing that, up to scaling, it has the unique property that the gradient flows resulting from this choice of energy do not depend on the normalization constant. For the metrics, we focus on variants of the Fisher-Rao, Wasserstein, and Stein metrics; we introduce the affine invariance property for gradient flows, and their corresponding mean-field models, determine whether a given metric leads to affine invariance, and modify it to make it affine invariant if it does not. We study the resulting gradient flows in both probability density space and Gaussian space. The flow in the Gaussian space may be understood as a Gaussian approximation of the flow. We demonstrate that the Gaussian approximation based on the metric and through moment closure coincide, establish connections between them, and study their long-time convergence properties showing the advantages of affine invariance.

PatchGT: Transformer over Non-trainable Clusters for Learning Graph Representations

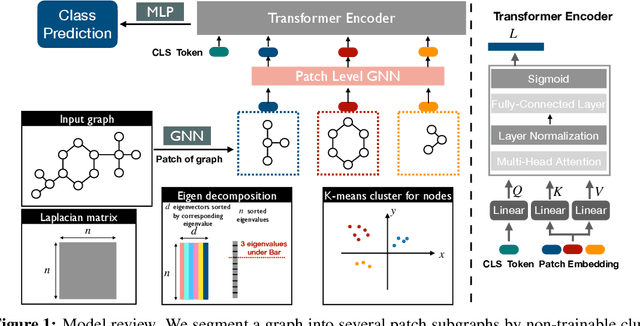
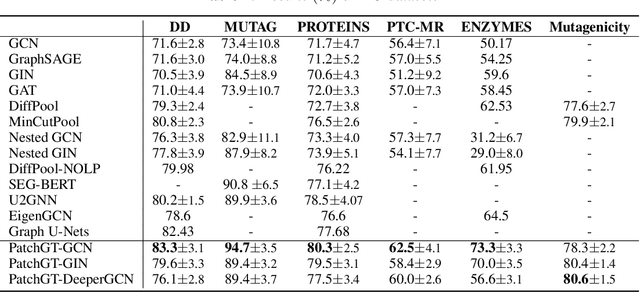
Recently the Transformer structure has shown good performances in graph learning tasks. However, these Transformer models directly work on graph nodes and may have difficulties learning high-level information. Inspired by the vision transformer, which applies to image patches, we propose a new Transformer-based graph neural network: Patch Graph Transformer (PatchGT). Unlike previous transformer-based models for learning graph representations, PatchGT learns from non-trainable graph patches, not from nodes directly. It can help save computation and improve the model performance. The key idea is to segment a graph into patches based on spectral clustering without any trainable parameters, with which the model can first use GNN layers to learn patch-level representations and then use Transformer to obtain graph-level representations. The architecture leverages the spectral information of graphs and combines the strengths of GNNs and Transformers. Further, we show the limitations of previous hierarchical trainable clusters theoretically and empirically. We also prove the proposed non-trainable spectral clustering method is permutation invariant and can help address the information bottlenecks in the graph. PatchGT achieves higher expressiveness than 1-WL-type GNNs, and the empirical study shows that PatchGT achieves competitive performances on benchmark datasets and provides interpretability to its predictions. The implementation of our algorithm is released at our Github repo: https://github.com/tufts-ml/PatchGT.

Robustness Implies Generalization via Data-Dependent Generalization Bounds

This paper proves that robustness implies generalization via data-dependent generalization bounds. As a result, robustness and generalization are shown to be connected closely in a data-dependent manner. Our bounds improve previous bounds in two directions, to solve an open problem that has seen little development since 2010. The first is to reduce the dependence on the covering number. The second is to remove the dependence on the hypothesis space. We present several examples, including ones for lasso and deep learning, in which our bounds are provably preferable. The experiments on real-world data and theoretical models demonstrate near-exponential improvements in various situations. To achieve these improvements, we do not require additional assumptions on the unknown distribution; instead, we only incorporate an observable and computable property of the training samples. A key technical innovation is an improved concentration bound for multinomial random variables that is of independent interest beyond robustness and generalization.