High-dimensional SGD aligns with emerging outlier eigenspaces

We rigorously study the joint evolution of training dynamics via stochastic gradient descent (SGD) and the spectra of empirical Hessian and gradient matrices. We prove that in two canonical classification tasks for multi-class high-dimensional mixtures and either 1 or 2-layer neural networks, the SGD trajectory rapidly aligns with emerging low-rank outlier eigenspaces of the Hessian and gradient matrices. Moreover, in multi-layer settings this alignment occurs per layer, with the final layer's outlier eigenspace evolving over the course of training, and exhibiting rank deficiency when the SGD converges to sub-optimal classifiers. This establishes some of the rich predictions that have arisen from extensive numerical studies in the last decade about the spectra of Hessian and information matrices over the course of training in overparametrized networks.

High-dimensional limit theorems for SGD: Effective dynamics and critical scaling

We study the scaling limits of stochastic gradient descent (SGD) with constant step-size in the high-dimensional regime. We prove limit theorems for the trajectories of summary statistics (i.e., finite-dimensional functions) of SGD as the dimension goes to infinity. Our approach allows one to choose the summary statistics that are tracked, the initialization, and the step-size. It yields both ballistic (ODE) and diffusive (SDE) limits, with the limit depending dramatically on the former choices. Interestingly, we find a critical scaling regime for the step-size below which the effective ballistic dynamics matches gradient flow for the population loss, but at which, a new correction term appears which changes the phase diagram. About the fixed points of this effective dynamics, the corresponding diffusive limits can be quite complex and even degenerate. We demonstrate our approach on popular examples including estimation for spiked matrix and tensor models and classification via two-layer networks for binary and XOR-type Gaussian mixture models. These examples exhibit surprising phenomena including multimodal timescales to convergence as well as convergence to sub-optimal solutions with probability bounded away from zero from random (e.g., Gaussian) initializations.

A classification for the performance of online SGD for high-dimensional inference

Stochastic gradient descent (SGD) is a popular algorithm for optimization problems arising in high-dimensional inference tasks. Here one produces an estimator of an unknown parameter from a large number of independent samples of data by iteratively optimizing a loss function. This loss function is high-dimensional, random, and often complex. We study here the performance of the simplest version of SGD, namely online SGD, in the initial "search" phase, where the algorithm is far from a trust region and the loss landscape is highly non-convex. To this end, we investigate the performance of online SGD at attaining a "better than random" correlation with the unknown parameter, i.e, achieving weak recovery. Our contribution is a classification of the difficulty of typical instances of this task for online SGD in terms of the number of samples required as the dimension diverges. This classification depends only on an intrinsic property of the population loss, which we call the information exponent. Using the information exponent, we find that there are three distinct regimes---the easy, critical, and difficult regimes---where one requires linear, quasilinear, and polynomially many samples (in the dimension) respectively to achieve weak recovery. We illustrate our approach by applying it to a wide variety of estimation tasks such as parameter estimation for generalized linear models, two-component Gaussian mixture models, phase retrieval, and spiked matrix and tensor models, as well as supervised learning for single-layer networks with general activation functions. In this latter case, our results translate into a classification of the difficulty of this task in terms of the Hermite decomposition of the activation function.

Complex energy landscapes in spiked-tensor and simple glassy models: ruggedness, arrangements of local minima and phase transitions

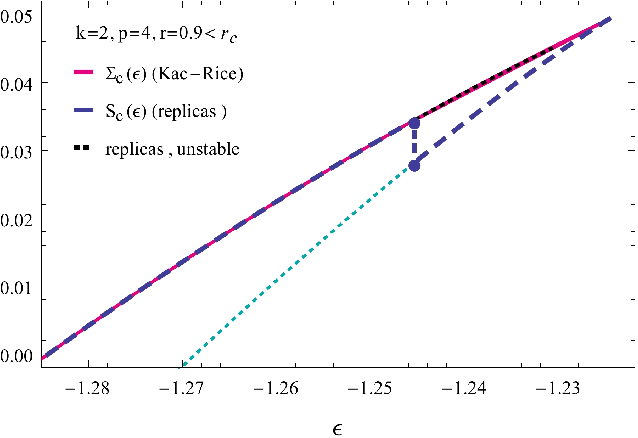
We study rough high-dimensional landscapes in which an increasingly stronger preference for a given configuration emerges. Such energy landscapes arise in glass physics and inference. In particular we focus on random Gaussian functions, and on the spiked-tensor model and generalizations. We thoroughly analyze the statistical properties of the corresponding landscapes and characterize the associated geometrical phase transitions. In order to perform our study, we develop a framework based on the Kac-Rice method that allows to compute the complexity of the landscape, i.e. the logarithm of the typical number of stationary points and their Hessian. This approach generalizes the one used to compute rigorously the annealed complexity of mean-field glass models. We discuss its advantages with respect to previous frameworks, in particular the thermodynamical replica method which is shown to lead to partially incorrect predictions.

The landscape of the spiked tensor model

We consider the problem of estimating a large rank-one tensor ${\boldsymbol u}^{\otimes k}\in({\mathbb R}^{n})^{\otimes k}$, $k\ge 3$ in Gaussian noise. Earlier work characterized a critical signal-to-noise ratio $\lambda_{Bayes}= O(1)$ above which an ideal estimator achieves strictly positive correlation with the unknown vector of interest. Remarkably no polynomial-time algorithm is known that achieved this goal unless $\lambda\ge C n^{(k-2)/4}$ and even powerful semidefinite programming relaxations appear to fail for $1\ll \lambda\ll n^{(k-2)/4}$. In order to elucidate this behavior, we consider the maximum likelihood estimator, which requires maximizing a degree-$k$ homogeneous polynomial over the unit sphere in $n$ dimensions. We compute the expected number of critical points and local maxima of this objective function and show that it is exponential in the dimensions $n$, and give exact formulas for the exponential growth rate. We show that (for $\lambda$ larger than a constant) critical points are either very close to the unknown vector ${\boldsymbol u}$, or are confined in a band of width $\Theta(\lambda^{-1/(k-1)})$ around the maximum circle that is orthogonal to ${\boldsymbol u}$. For local maxima, this band shrinks to be of size $\Theta(\lambda^{-1/(k-2)})$. These `uninformative' local maxima are likely to cause the failure of optimization algorithms.

Explorations on high dimensional landscapes

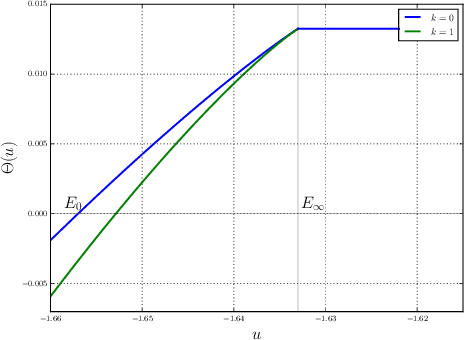
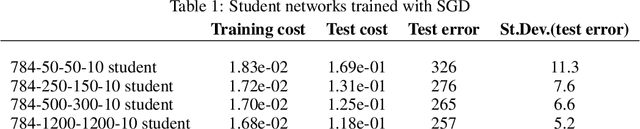
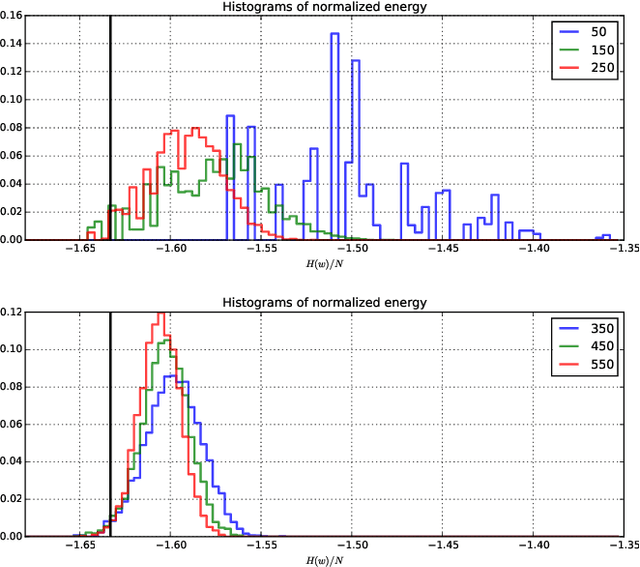
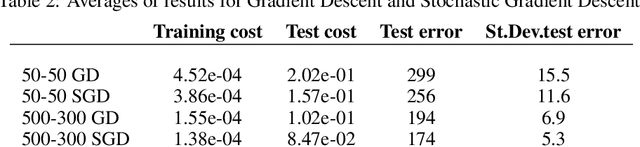
Finding minima of a real valued non-convex function over a high dimensional space is a major challenge in science. We provide evidence that some such functions that are defined on high dimensional domains have a narrow band of values whose pre-image contains the bulk of its critical points. This is in contrast with the low dimensional picture in which this band is wide. Our simulations agree with the previous theoretical work on spin glasses that proves the existence of such a band when the dimension of the domain tends to infinity. Furthermore our experiments on teacher-student networks with the MNIST dataset establish a similar phenomenon in deep networks. We finally observe that both the gradient descent and the stochastic gradient descent methods can reach this level within the same number of steps.