Empirical Analysis of the Hessian of Over-Parametrized Neural Networks

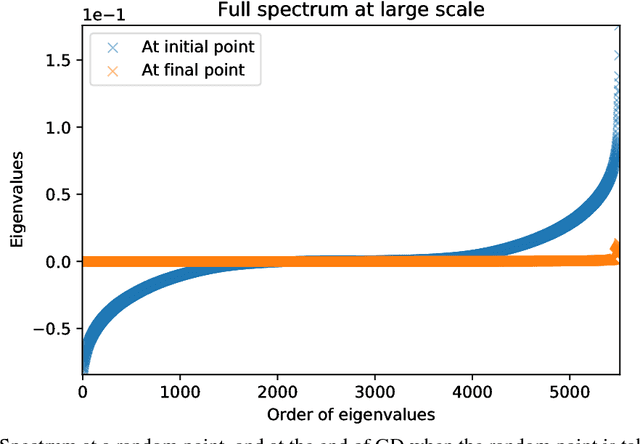
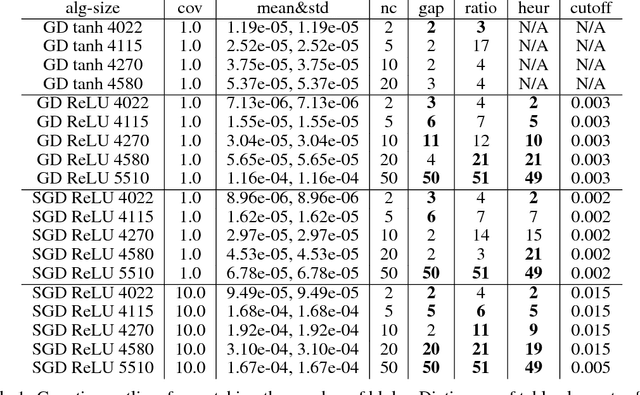
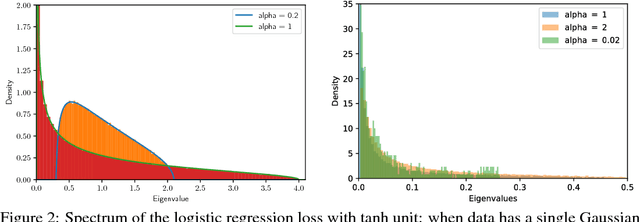
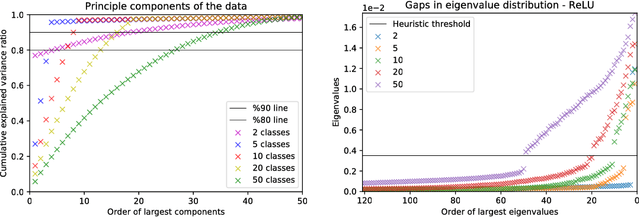
We study the properties of common loss surfaces through their Hessian matrix. In particular, in the context of deep learning, we empirically show that the spectrum of the Hessian is composed of two parts: (1) the bulk centered near zero, (2) and outliers away from the bulk. We present numerical evidence and mathematical justifications to the following conjectures laid out by Sagun et al. (2016): Fixing data, increasing the number of parameters merely scales the bulk of the spectrum; fixing the dimension and changing the data (for instance adding more clusters or making the data less separable) only affects the outliers. We believe that our observations have striking implications for non-convex optimization in high dimensions. First, the flatness of such landscapes (which can be measured by the singularity of the Hessian) implies that classical notions of basins of attraction may be quite misleading. And that the discussion of wide/narrow basins may be in need of a new perspective around over-parametrization and redundancy that are able to create large connected components at the bottom of the landscape. Second, the dependence of small number of large eigenvalues to the data distribution can be linked to the spectrum of the covariance matrix of gradients of model outputs. With this in mind, we may reevaluate the connections within the data-architecture-algorithm framework of a model, hoping that it would shed light into the geometry of high-dimensional and non-convex spaces in modern applications. In particular, we present a case that links the two observations: small and large batch gradient descent appear to converge to different basins of attraction but we show that they are in fact connected through their flat region and so belong to the same basin.

SearchQA: A New Q&A Dataset Augmented with Context from a Search Engine

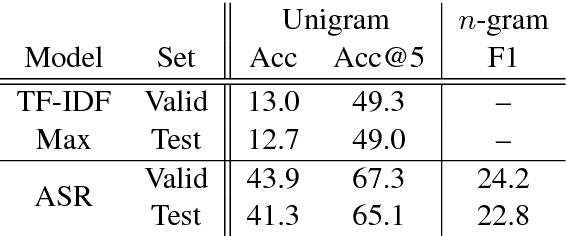
We publicly release a new large-scale dataset, called SearchQA, for machine comprehension, or question-answering. Unlike recently released datasets, such as DeepMind CNN/DailyMail and SQuAD, the proposed SearchQA was constructed to reflect a full pipeline of general question-answering. That is, we start not from an existing article and generate a question-answer pair, but start from an existing question-answer pair, crawled from J! Archive, and augment it with text snippets retrieved by Google. Following this approach, we built SearchQA, which consists of more than 140k question-answer pairs with each pair having 49.6 snippets on average. Each question-answer-context tuple of the SearchQA comes with additional meta-data such as the snippet's URL, which we believe will be valuable resources for future research. We conduct human evaluation as well as test two baseline methods, one simple word selection and the other deep learning based, on the SearchQA. We show that there is a meaningful gap between the human and machine performances. This suggests that the proposed dataset could well serve as a benchmark for question-answering.

Explorations on high dimensional landscapes

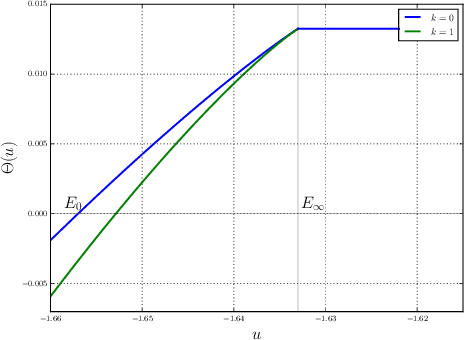
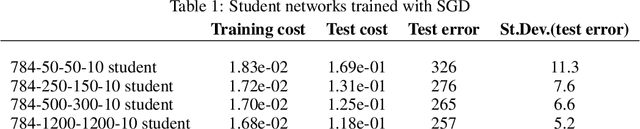
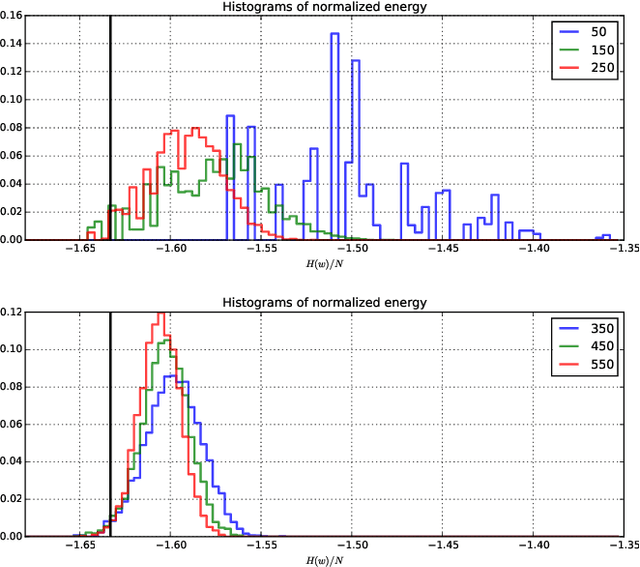
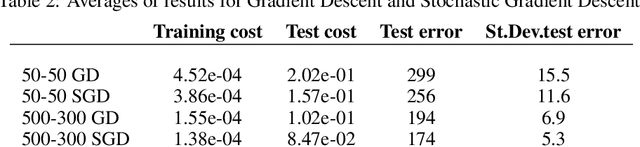
Finding minima of a real valued non-convex function over a high dimensional space is a major challenge in science. We provide evidence that some such functions that are defined on high dimensional domains have a narrow band of values whose pre-image contains the bulk of its critical points. This is in contrast with the low dimensional picture in which this band is wide. Our simulations agree with the previous theoretical work on spin glasses that proves the existence of such a band when the dimension of the domain tends to infinity. Furthermore our experiments on teacher-student networks with the MNIST dataset establish a similar phenomenon in deep networks. We finally observe that both the gradient descent and the stochastic gradient descent methods can reach this level within the same number of steps.