MagicPIG: LSH Sampling for Efficient LLM Generation

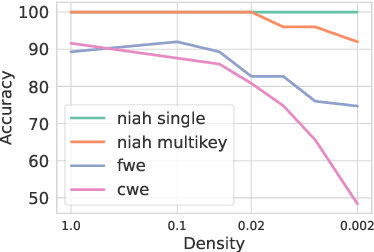
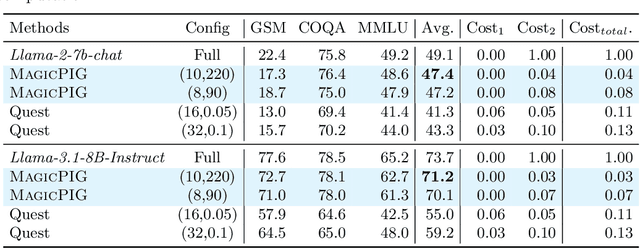
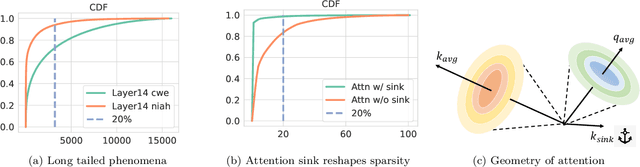
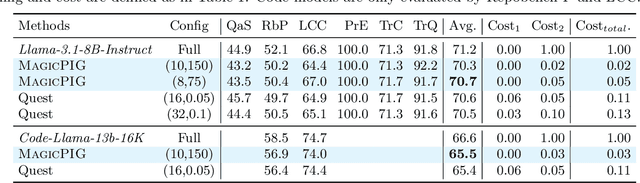
Large language models (LLMs) with long context windows have gained significant attention. However, the KV cache, stored to avoid re-computation, becomes a bottleneck. Various dynamic sparse or TopK-based attention approximation methods have been proposed to leverage the common insight that attention is sparse. In this paper, we first show that TopK attention itself suffers from quality degradation in certain downstream tasks because attention is not always as sparse as expected. Rather than selecting the keys and values with the highest attention scores, sampling with theoretical guarantees can provide a better estimation for attention output. To make the sampling-based approximation practical in LLM generation, we propose MagicPIG, a heterogeneous system based on Locality Sensitive Hashing (LSH). MagicPIG significantly reduces the workload of attention computation while preserving high accuracy for diverse tasks. MagicPIG stores the LSH hash tables and runs the attention computation on the CPU, which allows it to serve longer contexts and larger batch sizes with high approximation accuracy. MagicPIG can improve decoding throughput by $1.9\sim3.9\times$ across various GPU hardware and achieve 110ms decoding latency on a single RTX 4090 for Llama-3.1-8B-Instruct model with a context of 96k tokens. The code is available at \url{https://github.com/Infini-AI-Lab/MagicPIG}.

Birth of a Transformer: A Memory Viewpoint

Large language models based on transformers have achieved great empirical successes. However, as they are deployed more widely, there is a growing need to better understand their internal mechanisms in order to make them more reliable. These models appear to store vast amounts of knowledge from their training data, and to adapt quickly to new information provided in their context or prompt. We study how transformers balance these two types of knowledge by considering a synthetic setup where tokens are generated from either global or context-specific bigram distributions. By a careful empirical analysis of the training process on a simplified two-layer transformer, we illustrate the fast learning of global bigrams and the slower development of an "induction head" mechanism for the in-context bigrams. We highlight the role of weight matrices as associative memories, provide theoretical insights on how gradients enable their learning during training, and study the role of data-distributional properties.

Active Self-Supervised Learning: A Few Low-Cost Relationships Are All You Need

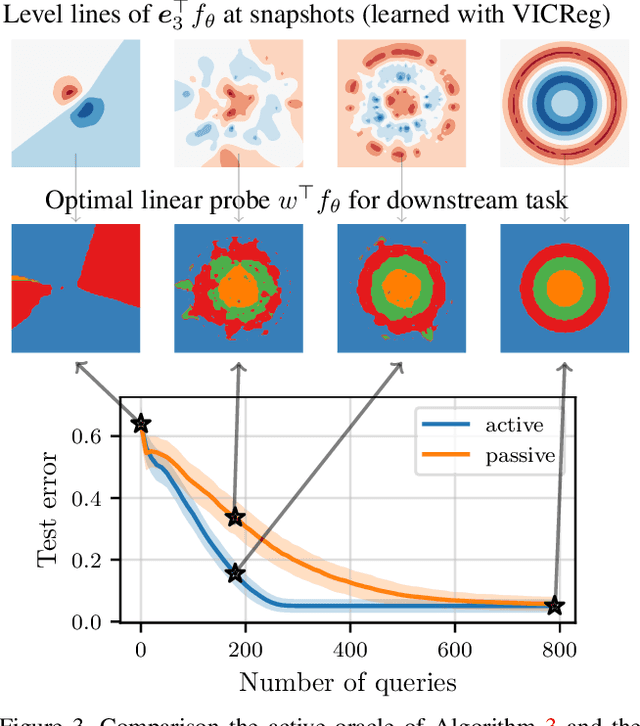
Self-Supervised Learning (SSL) has emerged as the solution of choice to learn transferable representations from unlabeled data. However, SSL requires to build samples that are known to be semantically akin, i.e. positive views. Requiring such knowledge is the main limitation of SSL and is often tackled by ad-hoc strategies e.g. applying known data-augmentations to the same input. In this work, we generalize and formalize this principle through Positive Active Learning (PAL) where an oracle queries semantic relationships between samples. PAL achieves three main objectives. First, it unveils a theoretically grounded learning framework beyond SSL, that can be extended to tackle supervised and semi-supervised learning depending on the employed oracle. Second, it provides a consistent algorithm to embed a priori knowledge, e.g. some observed labels, into any SSL losses without any change in the training pipeline. Third, it provides a proper active learning framework yielding low-cost solutions to annotate datasets, arguably bringing the gap between theory and practice of active learning that is based on simple-to-answer-by-non-experts queries of semantic relationships between inputs.

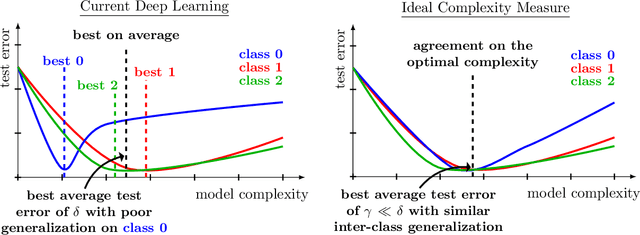
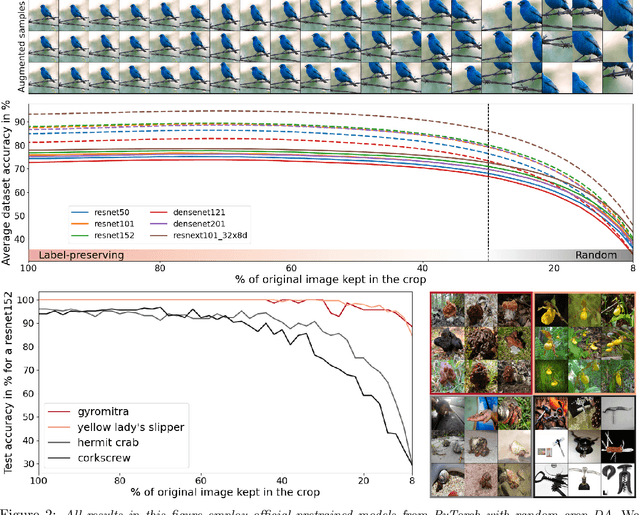
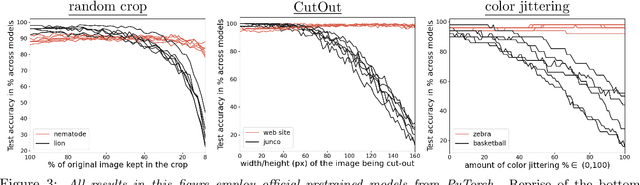
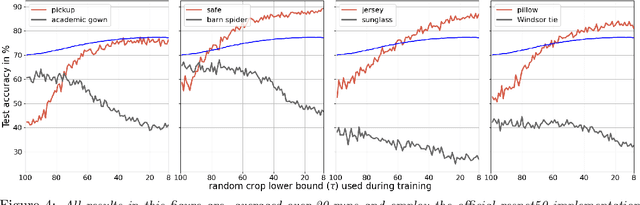
The Effects of Regularization and Data Augmentation are Class Dependent

Regularization is a fundamental technique to prevent over-fitting and to improve generalization performances by constraining a model's complexity. Current Deep Networks heavily rely on regularizers such as Data-Augmentation (DA) or weight-decay, and employ structural risk minimization, i.e. cross-validation, to select the optimal regularization hyper-parameters. In this study, we demonstrate that techniques such as DA or weight decay produce a model with a reduced complexity that is unfair across classes. The optimal amount of DA or weight decay found from cross-validation leads to disastrous model performances on some classes e.g. on Imagenet with a resnet50, the "barn spider" classification test accuracy falls from $68\%$ to $46\%$ only by introducing random crop DA during training. Even more surprising, such performance drop also appears when introducing uninformative regularization techniques such as weight decay. Those results demonstrate that our search for ever increasing generalization performance -- averaged over all classes and samples -- has left us with models and regularizers that silently sacrifice performances on some classes. This scenario can become dangerous when deploying a model on downstream tasks e.g. an Imagenet pre-trained resnet50 deployed on INaturalist sees its performances fall from $70\%$ to $30\%$ on class \#8889 when introducing random crop DA during the Imagenet pre-training phase. Those results demonstrate that designing novel regularizers without class-dependent bias remains an open research question.

An Attract-Repel Decomposition of Undirected Networks

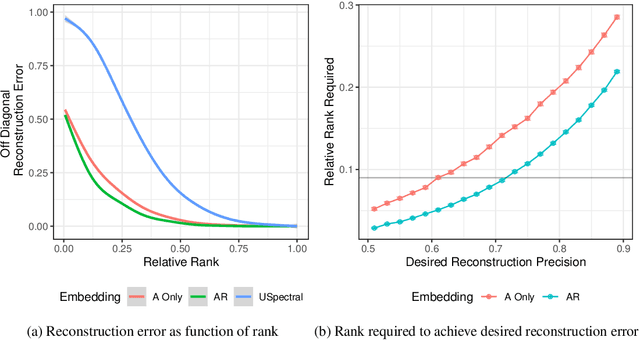
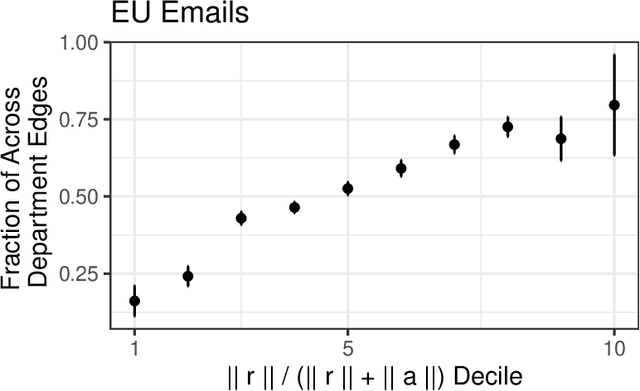
Dot product latent space embedding is a common form of representation learning in undirected graphs (e.g. social networks, co-occurrence networks). We show that such models have problems dealing with 'intransitive' situations where A is linked to B, B is linked to C but A is not linked to C. Such situations occur in social networks when opposites attract (heterophily) and in co-occurrence networks when there are substitute nodes (e.g. the presence of Pepsi or Coke, but rarely both, in otherwise similar purchase baskets). We present a simple expansion which we call the attract-repel (AR) decomposition: a set of latent attributes on which similar nodes attract and another set of latent attributes on which similar nodes repel. We demonstrate the AR decomposition in real social networks and show that it can be used to measure the amount of latent homophily and heterophily. In addition, it can be applied to co-occurrence networks to discover roles in teams and find substitutable ingredients in recipes.

Linear unit-tests for invariance discovery

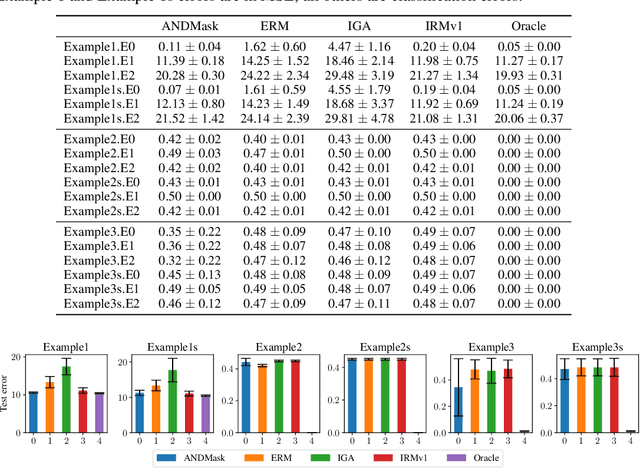
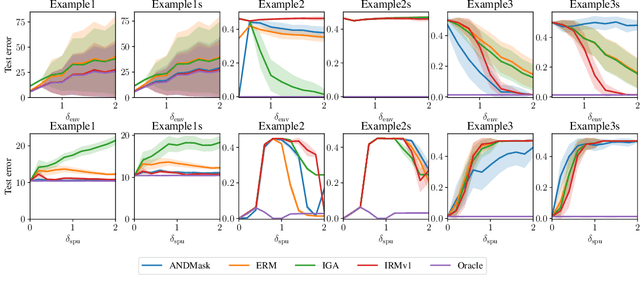
There is an increasing interest in algorithms to learn invariant correlations across training environments. A big share of the current proposals find theoretical support in the causality literature but, how useful are they in practice? The purpose of this note is to propose six linear low-dimensional problems -- unit tests -- to evaluate different types of out-of-distribution generalization in a precise manner. Following initial experiments, none of the three recently proposed alternatives passes all tests. By providing the code to automatically replicate all the results in this manuscript (https://www.github.com/facebookresearch/InvarianceUnitTests), we hope that our unit tests become a standard steppingstone for researchers in out-of-distribution generalization.

AdaGrad stepsizes: Sharp convergence over nonconvex landscapes, from any initialization

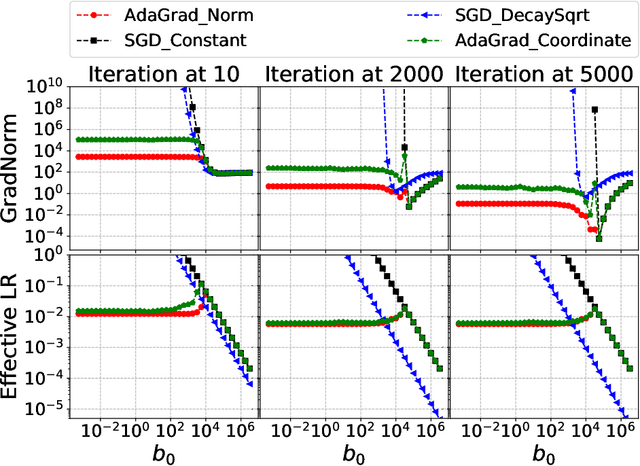
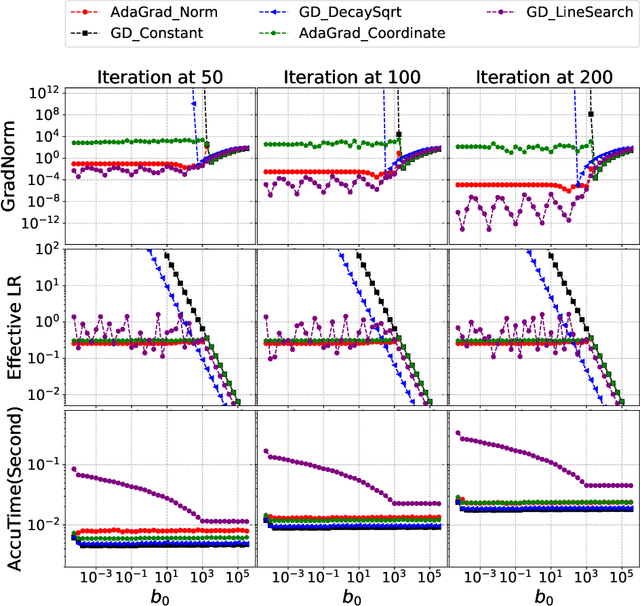
Adaptive gradient methods such as AdaGrad and its variants update the stepsize in stochastic gradient descent on the fly according to the gradients received along the way; such methods have gained widespread use in large-scale optimization for their ability to converge robustly, without the need to fine tune parameters such as the stepsize schedule. Yet, the theoretical guarantees to date for AdaGrad are for online and convex optimization, which is quite different from the offline and nonconvex setting where adaptive gradient methods shine in practice. We bridge this gap by providing strong theoretical guarantees in batch and stochastic setting, for the convergence of AdaGrad over smooth, nonconvex landscapes, from any initialization of the stepsize, without knowledge of Lipschitz constant of the gradient. We show in the stochastic setting that AdaGrad converges to a stationary point at the optimal $O(1/\sqrt{N})$ rate (up to a $\log(N)$ factor), and in the batch setting, at the optimal $O(1/N)$ rate. Moreover, in both settings, the constant in the rate matches the constant obtained as if the variance of the gradient noise and Lipschitz constant of the gradient were known in advance and used to tune the stepsize, up to a logarithmic factor of the mismatch between the optimal stepsize and the stepsize used to initialize AdaGrad. In particular, our results imply that AdaGrad is robust to both the unknown Lipschitz constant and level of stochastic noise on the gradient, in a near-optimal sense. When there is noise, AdaGrad converges at the rate of $O(1/\sqrt{N})$ with well-tuned stepsize, and when there is not noise, the same algorithm converges at the rate of $O(1/N)$ like well-tuned batch gradient descent.

Empirical Analysis of the Hessian of Over-Parametrized Neural Networks

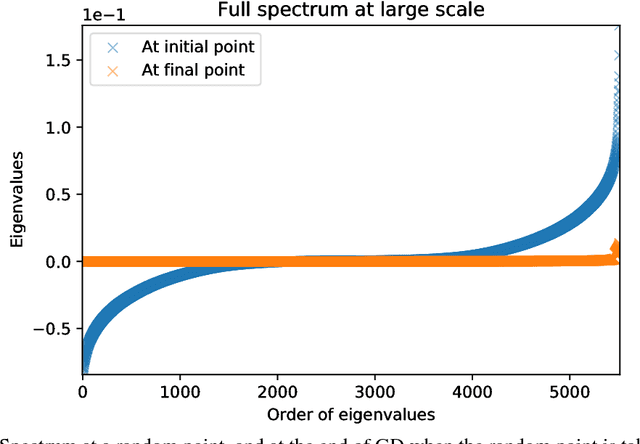
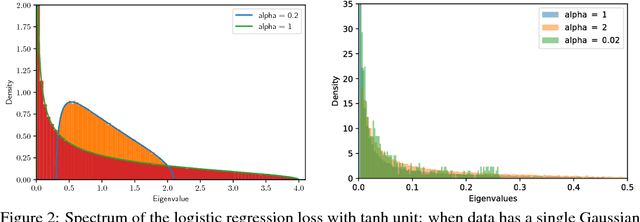
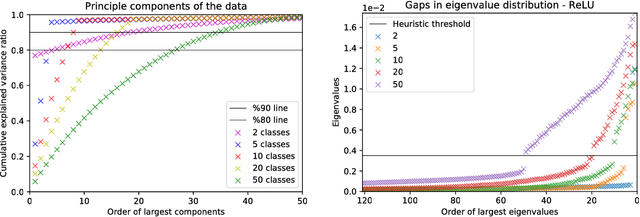
We study the properties of common loss surfaces through their Hessian matrix. In particular, in the context of deep learning, we empirically show that the spectrum of the Hessian is composed of two parts: (1) the bulk centered near zero, (2) and outliers away from the bulk. We present numerical evidence and mathematical justifications to the following conjectures laid out by Sagun et al. (2016): Fixing data, increasing the number of parameters merely scales the bulk of the spectrum; fixing the dimension and changing the data (for instance adding more clusters or making the data less separable) only affects the outliers. We believe that our observations have striking implications for non-convex optimization in high dimensions. First, the flatness of such landscapes (which can be measured by the singularity of the Hessian) implies that classical notions of basins of attraction may be quite misleading. And that the discussion of wide/narrow basins may be in need of a new perspective around over-parametrization and redundancy that are able to create large connected components at the bottom of the landscape. Second, the dependence of small number of large eigenvalues to the data distribution can be linked to the spectrum of the covariance matrix of gradients of model outputs. With this in mind, we may reevaluate the connections within the data-architecture-algorithm framework of a model, hoping that it would shed light into the geometry of high-dimensional and non-convex spaces in modern applications. In particular, we present a case that links the two observations: small and large batch gradient descent appear to converge to different basins of attraction but we show that they are in fact connected through their flat region and so belong to the same basin.

Geometrical Insights for Implicit Generative Modeling

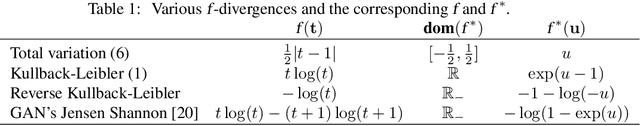
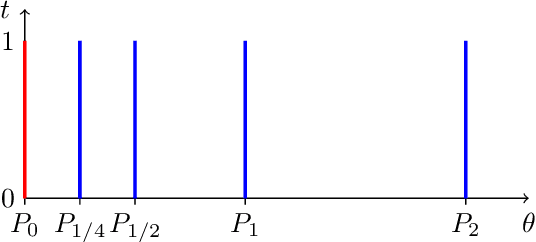
Learning algorithms for implicit generative models can optimize a variety of criteria that measure how the data distribution differs from the implicit model distribution, including the Wasserstein distance, the Energy distance, and the Maximum Mean Discrepancy criterion. A careful look at the geometries induced by these distances on the space of probability measures reveals interesting differences. In particular, we can establish surprising approximate global convergence guarantees for the $1$-Wasserstein distance,even when the parametric generator has a nonconvex parametrization.

Eigenvalues of the Hessian in Deep Learning: Singularity and Beyond

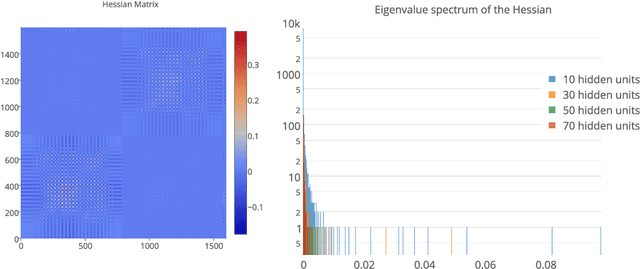
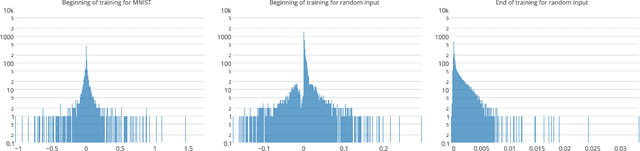
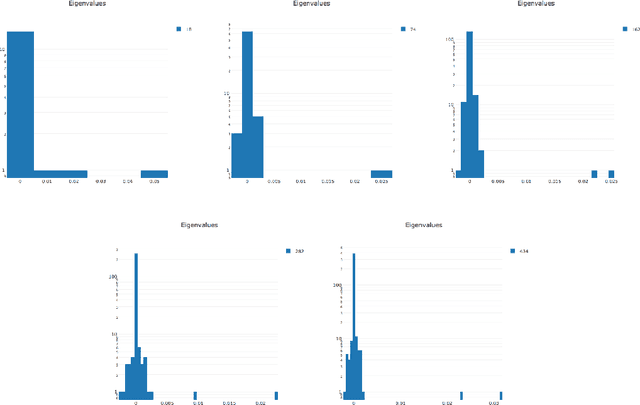
We look at the eigenvalues of the Hessian of a loss function before and after training. The eigenvalue distribution is seen to be composed of two parts, the bulk which is concentrated around zero, and the edges which are scattered away from zero. We present empirical evidence for the bulk indicating how over-parametrized the system is, and for the edges that depend on the input data.