Controllable Shadow Generation with Single-Step Diffusion Models from Synthetic Data

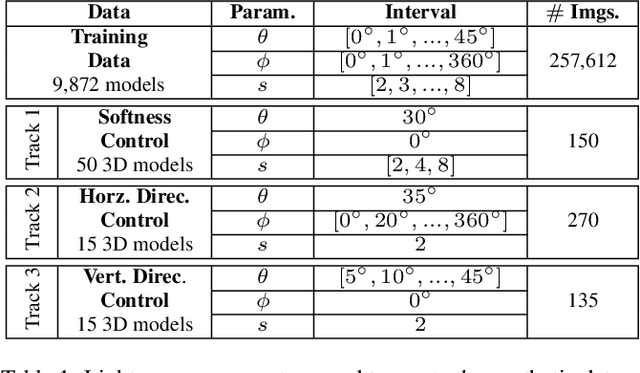
Realistic shadow generation is a critical component for high-quality image compositing and visual effects, yet existing methods suffer from certain limitations: Physics-based approaches require a 3D scene geometry, which is often unavailable, while learning-based techniques struggle with control and visual artifacts. We introduce a novel method for fast, controllable, and background-free shadow generation for 2D object images. We create a large synthetic dataset using a 3D rendering engine to train a diffusion model for controllable shadow generation, generating shadow maps for diverse light source parameters. Through extensive ablation studies, we find that rectified flow objective achieves high-quality results with just a single sampling step enabling real-time applications. Furthermore, our experiments demonstrate that the model generalizes well to real-world images. To facilitate further research in evaluating quality and controllability in shadow generation, we release a new public benchmark containing a diverse set of object images and shadow maps in various settings. The project page is available at https://gojasper.github.io/controllable-shadow-generation-project/

Flash Diffusion: Accelerating Any Conditional Diffusion Model for Few Steps Image Generation

In this paper, we propose an efficient, fast, and versatile distillation method to accelerate the generation of pre-trained diffusion models: Flash Diffusion. The method reaches state-of-the-art performances in terms of FID and CLIP-Score for few steps image generation on the COCO2014 and COCO2017 datasets, while requiring only several GPU hours of training and fewer trainable parameters than existing methods. In addition to its efficiency, the versatility of the method is also exposed across several tasks such as text-to-image, inpainting, face-swapping, super-resolution and using different backbones such as UNet-based denoisers (SD1.5, SDXL) or DiT (Pixart-$\alpha$), as well as adapters. In all cases, the method allowed to reduce drastically the number of sampling steps while maintaining very high-quality image generation. The official implementation is available at https://github.com/gojasper/flash-diffusion.

Mean-field methods and algorithmic perspectives for high-dimensional machine learning

The main difficulty that arises in the analysis of most machine learning algorithms is to handle, analytically and numerically, a large number of interacting random variables. In this Ph.D manuscript, we revisit an approach based on the tools of statistical physics of disordered systems. Developed through a rich literature, they have been precisely designed to infer the macroscopic behavior of a large number of particles from their microscopic interactions. At the heart of this work, we strongly capitalize on the deep connection between the replica method and message passing algorithms in order to shed light on the phase diagrams of various theoretical models, with an emphasis on the potential differences between statistical and algorithmic thresholds. We essentially focus on synthetic tasks and data generated in the teacher-student paradigm. In particular, we apply these mean-field methods to the Bayes-optimal analysis of committee machines, to the worst-case analysis of Rademacher generalization bounds for perceptrons, and to empirical risk minimization in the context of generalized linear models. Finally, we develop a framework to analyze estimation models with structured prior informations, produced for instance by deep neural networks based generative models with random weights.

Linear unit-tests for invariance discovery

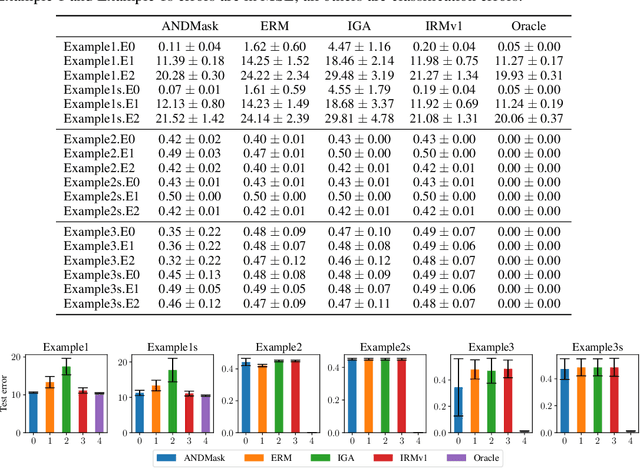
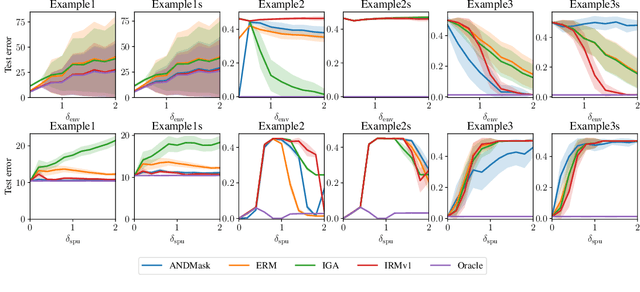
There is an increasing interest in algorithms to learn invariant correlations across training environments. A big share of the current proposals find theoretical support in the causality literature but, how useful are they in practice? The purpose of this note is to propose six linear low-dimensional problems -- unit tests -- to evaluate different types of out-of-distribution generalization in a precise manner. Following initial experiments, none of the three recently proposed alternatives passes all tests. By providing the code to automatically replicate all the results in this manuscript (https://www.github.com/facebookresearch/InvarianceUnitTests), we hope that our unit tests become a standard steppingstone for researchers in out-of-distribution generalization.

Generalization error in high-dimensional perceptrons: Approaching Bayes error with convex optimization

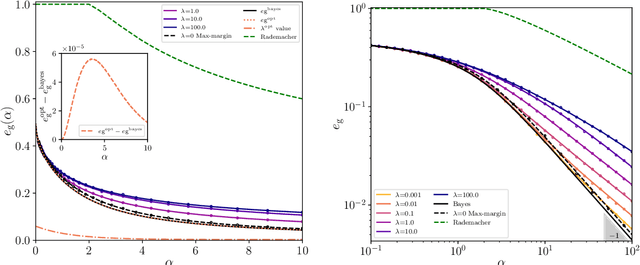
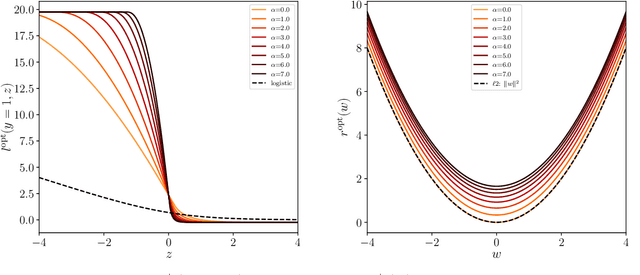
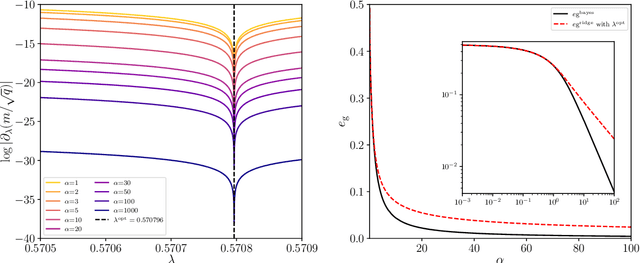
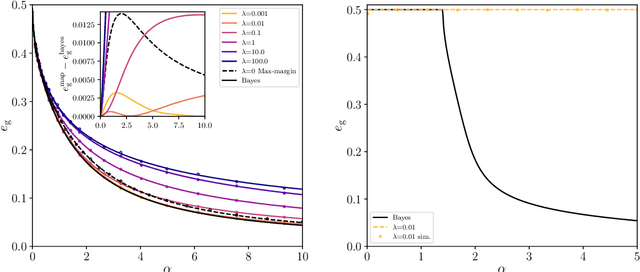
We consider a commonly studied supervised classification of a synthetic dataset whose labels are generated by feeding a one-layer neural network with random iid inputs. We study the generalization performances of standard classifiers in the high-dimensional regime where $\alpha=n/d$ is kept finite in the limit of a high dimension $d$ and number of samples $n$. Our contribution is three-fold: First, we prove a formula for the generalization error achieved by $\ell_2$ regularized classifiers that minimize a convex loss. This formula was first obtained by the heuristic replica method of statistical physics. Secondly, focussing on commonly used loss functions and optimizing the $\ell_2$ regularization strength, we observe that while ridge regression performance is poor, logistic and hinge regression are surprisingly able to approach the Bayes-optimal generalization error extremely closely. As $\alpha \to \infty$ they lead to Bayes-optimal rates, a fact that does not follow from predictions of margin-based generalization error bounds. Third, we design an optimal loss and regularizer that provably leads to Bayes-optimal generalization error.

TRAMP: Compositional Inference with TRee Approximate Message Passing

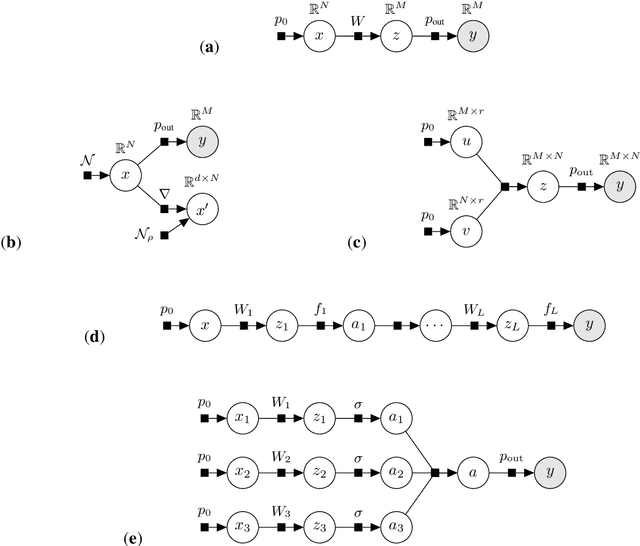
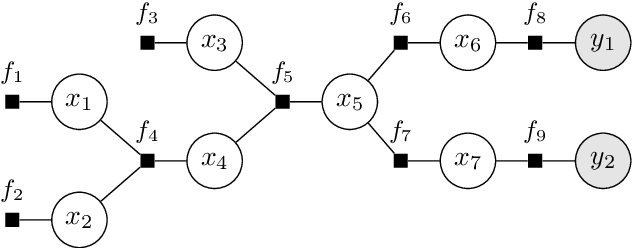
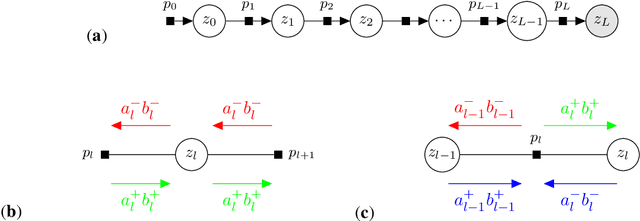
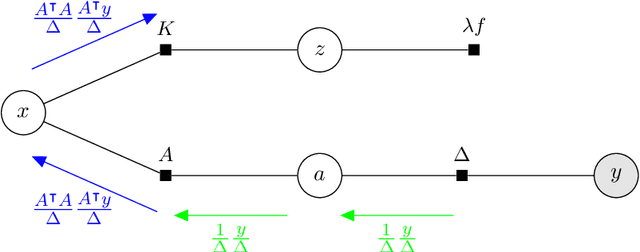
We introduce tramp, standing for TRee Approximate Message Passing, a python package for compositional inference in high-dimensional tree-structured models. The package provides an unifying framework to study several approximate message passing algorithms previously derived for a variety of machine learning tasks such as generalized linear models, inference in multi-layer networks, matrix factorization, and reconstruction using non-separable penalties. For some models, the asymptotic performance of the algorithm can be theoretically predicted by the state evolution, and the measurements entropy estimated by the free entropy formalism. The implementation is modular by design: each module, which implements a factor, can be composed at will with other modules to solve complex inference tasks. The user only needs to declare the factor graph of the model: the inference algorithm, state evolution and entropy estimation are fully automated.

Rademacher complexity and spin glasses: A link between the replica and statistical theories of learning

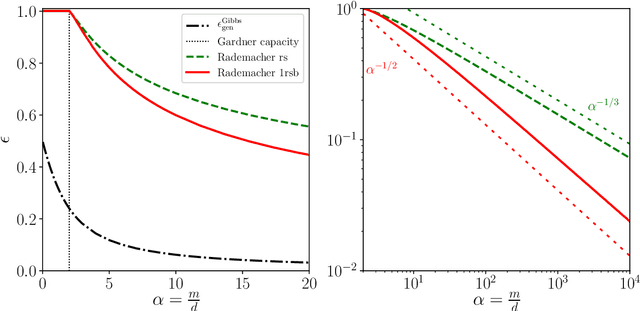
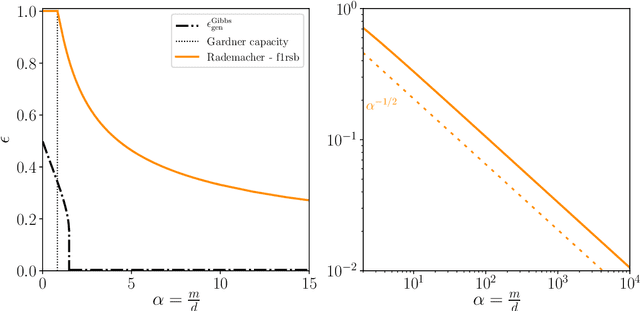
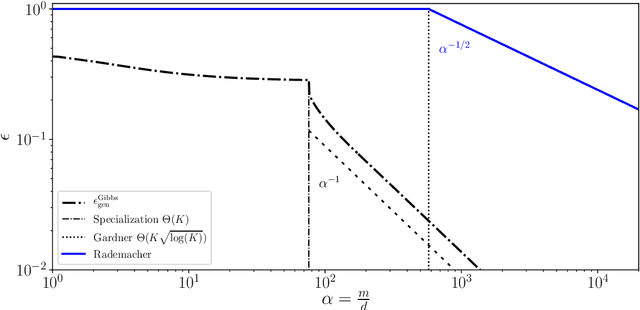
Statistical learning theory provides bounds of the generalization gap, using in particular the Vapnik-Chervonenkis dimension and the Rademacher complexity. An alternative approach, mainly studied in the statistical physics literature, is the study of generalization in simple synthetic-data models. Here we discuss the connections between these approaches and focus on the link between the Rademacher complexity in statistical learning and the theories of generalization for typical-case synthetic models from statistical physics, involving quantities known as Gardner capacity and ground state energy. We show that in these models the Rademacher complexity is closely related to the ground state energy computed by replica theories. Using this connection, one may reinterpret many results of the literature as rigorous Rademacher bounds in a variety of models in the high-dimensional statistics limit. Somewhat surprisingly, we also show that statistical learning theory provides predictions for the behavior of the ground-state energies in some full replica symmetry breaking models.

Exact asymptotics for phase retrieval and compressed sensing with random generative priors

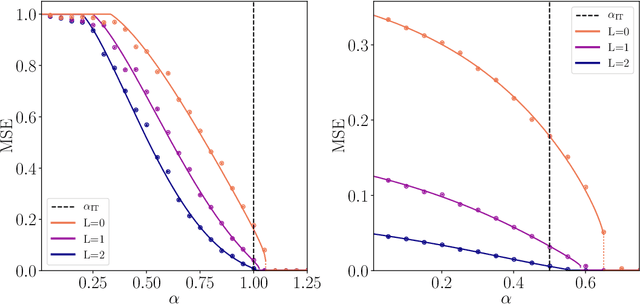
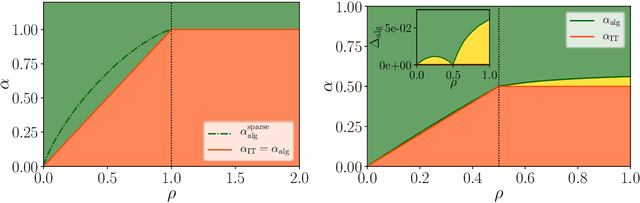
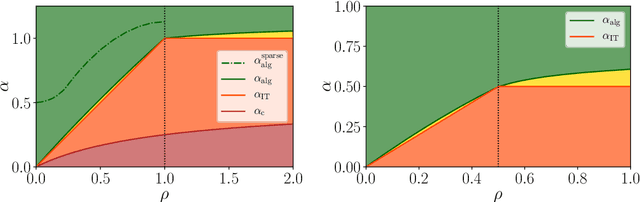
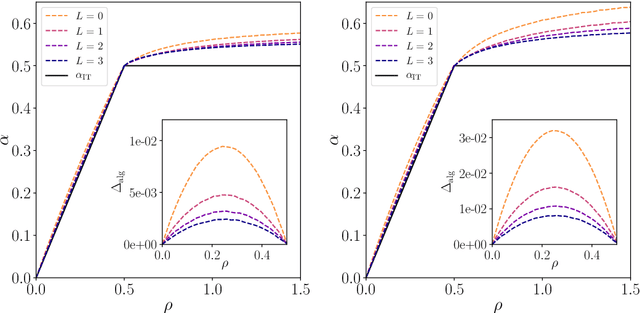
We consider the problem of compressed sensing and of (real-valued) phase retrieval with random measurement matrix. We derive sharp asymptotics for the information-theoretically optimal performance and for the best known polynomial algorithm for an ensemble of generative priors consisting of fully connected deep neural networks with random weight matrices and arbitrary activations. We compare the performance to sparse separable priors and conclude that generative priors might be advantageous in terms of algorithmic performance. In particular, while sparsity does not allow to perform compressive phase retrieval efficiently close to its information-theoretic limit, it is found that under the random generative prior compressed phase retrieval becomes tractable.

The spiked matrix model with generative priors

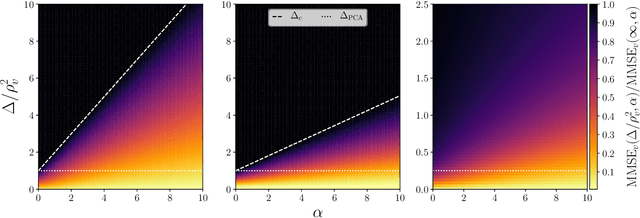
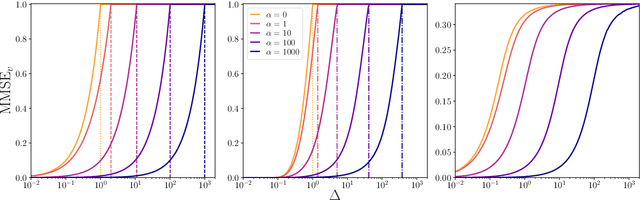
Using a low-dimensional parametrization of signals is a generic and powerful way to enhance performance in signal processing and statistical inference. A very popular and widely explored type of dimensionality reduction is sparsity; another type is generative modelling of signal distributions. Generative models based on neural networks, such as GANs or variational auto-encoders, are particularly performant and are gaining on applicability. In this paper we study spiked matrix models, where a low-rank matrix is observed through a noisy channel. This problem with sparse structure of the spikes has attracted broad attention in the past literature. Here, we replace the sparsity assumption by generative modelling, and investigate the consequences on statistical and algorithmic properties. We analyze the Bayes-optimal performance under specific generative models for the spike. In contrast with the sparsity assumption, we do not observe regions of parameters where statistical performance is superior to the best known algorithmic performance. We show that in the analyzed cases the approximate message passing algorithm is able to reach optimal performance. We also design enhanced spectral algorithms and analyze their performance and thresholds using random matrix theory, showing their superiority to the classical principal component analysis. We complement our theoretical results by illustrating the performance of the spectral algorithms when the spikes come from real datasets.

The committee machine: Computational to statistical gaps in learning a two-layers neural network

Heuristic tools from statistical physics have been used in the past to locate the phase transitions and compute the optimal learning and generalization errors in the teacher-student scenario in multi-layer neural networks. In this contribution, we provide a rigorous justification of these approaches for a two-layers neural network model called the committee machine. We also introduce a version of the approximate message passing (AMP) algorithm for the committee machine that allows to perform optimal learning in polynomial time for a large set of parameters. We find that there are regimes in which a low generalization error is information-theoretically achievable while the AMP algorithm fails to deliver it, strongly suggesting that no efficient algorithm exists for those cases, and unveiling a large computational gap.