Antoine Baker
SiMCa: Sinkhorn Matrix Factorization with Capacity Constraints
Mar 18, 2022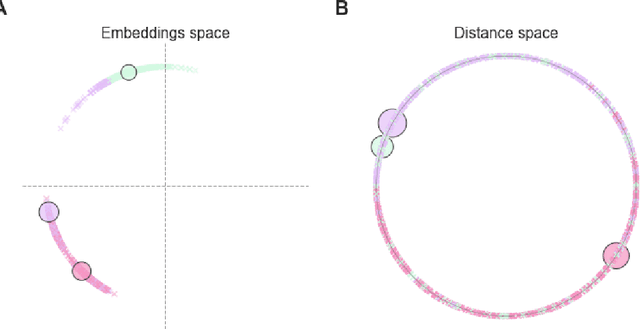
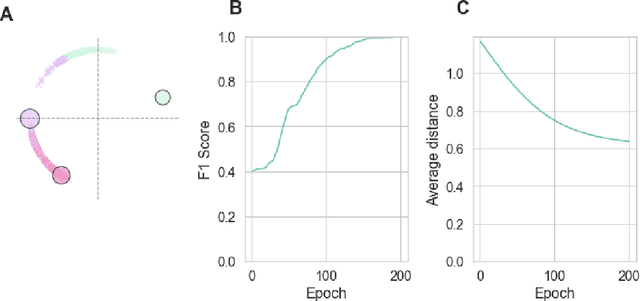
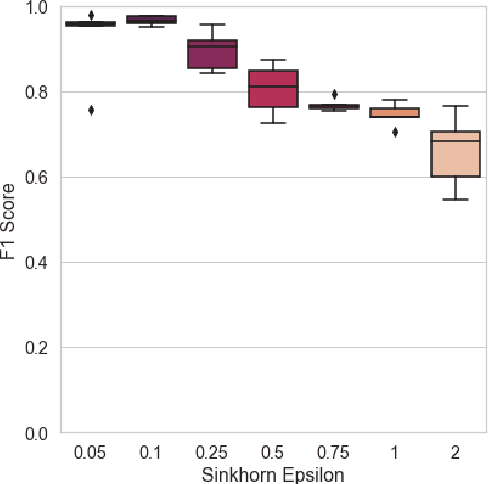
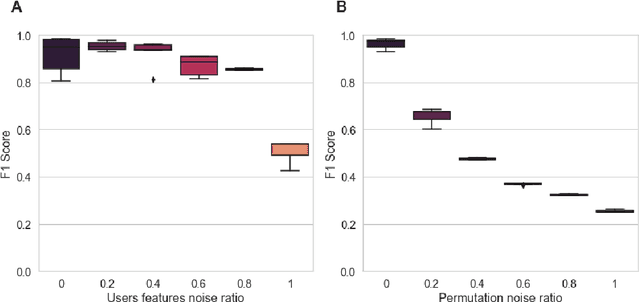
Abstract:For a very broad range of problems, recommendation algorithms have been increasingly used over the past decade. In most of these algorithms, the predictions are built upon user-item affinity scores which are obtained from high-dimensional embeddings of items and users. In more complex scenarios, with geometrical or capacity constraints, prediction based on embeddings may not be sufficient and some additional features should be considered in the design of the algorithm. In this work, we study the recommendation problem in the setting where affinities between users and items are based both on their embeddings in a latent space and on their geographical distance in their underlying euclidean space (e.g., $\mathbb{R}^2$), together with item capacity constraints. This framework is motivated by some real-world applications, for instance in healthcare: the task is to recommend hospitals to patients based on their location, pathology, and hospital capacities. In these applications, there is somewhat of an asymmetry between users and items: items are viewed as static points, their embeddings, capacities and locations constraining the allocation. Upon the observation of an optimal allocation, user embeddings, items capacities, and their positions in their underlying euclidean space, our aim is to recover item embeddings in the latent space; doing so, we are then able to use this estimate e.g. in order to predict future allocations. We propose an algorithm (SiMCa) based on matrix factorization enhanced with optimal transport steps to model user-item affinities and learn item embeddings from observed data. We then illustrate and discuss the results of such an approach for hospital recommendation on synthetic data.
Epidemic mitigation by statistical inference from contact tracing data
Sep 20, 2020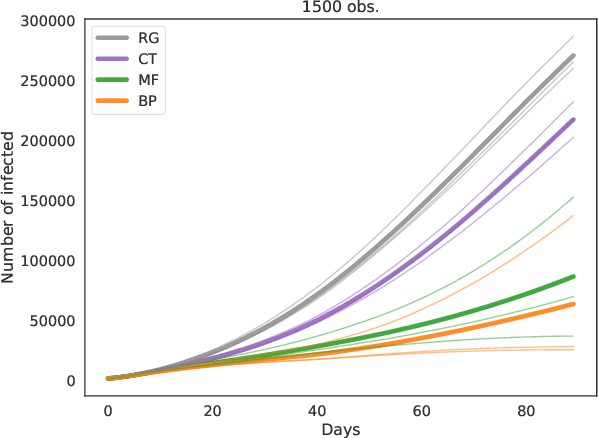
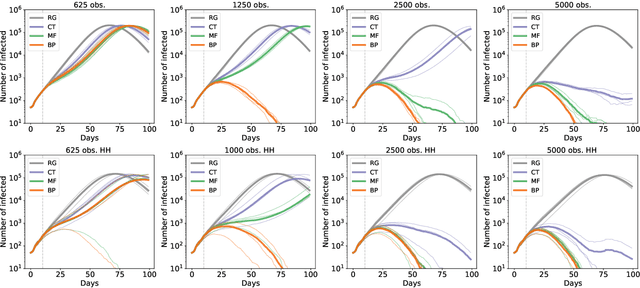
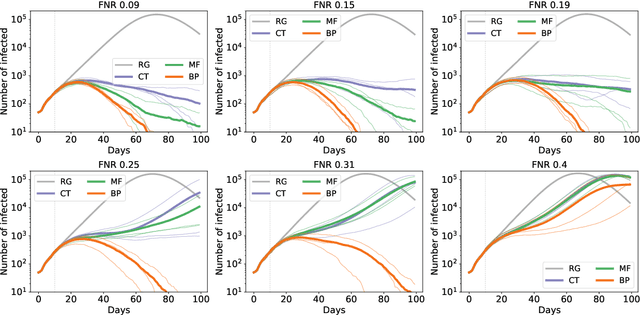

Abstract:Contact-tracing is an essential tool in order to mitigate the impact of pandemic such as the COVID-19. In order to achieve efficient and scalable contact-tracing in real time, digital devices can play an important role. While a lot of attention has been paid to analyzing the privacy and ethical risks of the associated mobile applications, so far much less research has been devoted to optimizing their performance and assessing their impact on the mitigation of the epidemic. We develop Bayesian inference methods to estimate the risk that an individual is infected. This inference is based on the list of his recent contacts and their own risk levels, as well as personal information such as results of tests or presence of syndromes. We propose to use probabilistic risk estimation in order to optimize testing and quarantining strategies for the control of an epidemic. Our results show that in some range of epidemic spreading (typically when the manual tracing of all contacts of infected people becomes practically impossible, but before the fraction of infected people reaches the scale where a lock-down becomes unavoidable), this inference of individuals at risk could be an efficient way to mitigate the epidemic. Our approaches translate into fully distributed algorithms that only require communication between individuals who have recently been in contact. Such communication may be encrypted and anonymized and thus compatible with privacy preserving standards. We conclude that probabilistic risk estimation is capable to enhance performance of digital contact tracing and should be considered in the currently developed mobile applications.
TRAMP: Compositional Inference with TRee Approximate Message Passing
Apr 03, 2020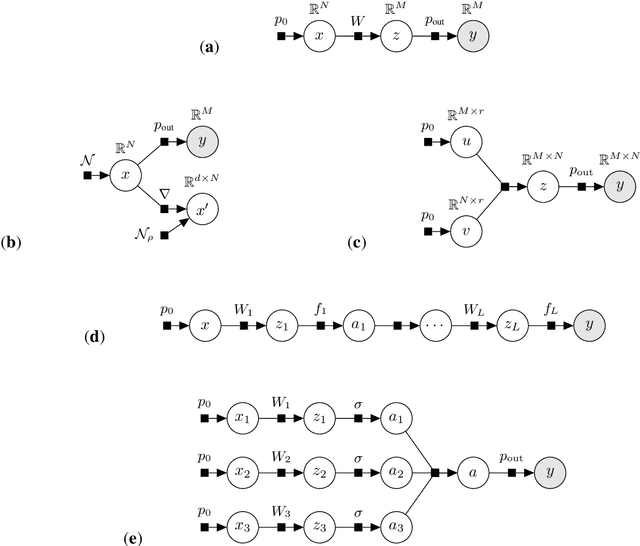
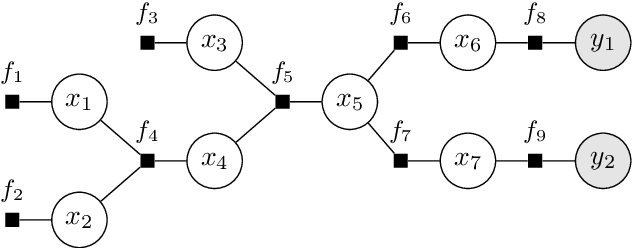
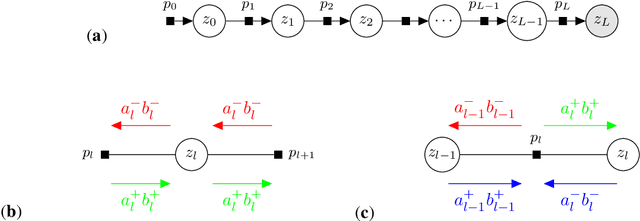
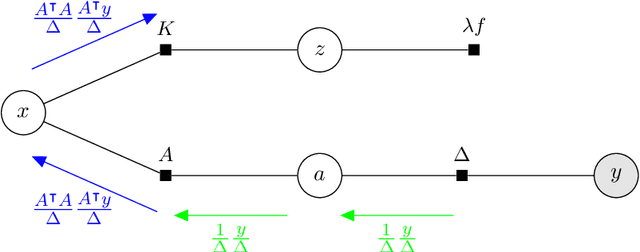
Abstract:We introduce tramp, standing for TRee Approximate Message Passing, a python package for compositional inference in high-dimensional tree-structured models. The package provides an unifying framework to study several approximate message passing algorithms previously derived for a variety of machine learning tasks such as generalized linear models, inference in multi-layer networks, matrix factorization, and reconstruction using non-separable penalties. For some models, the asymptotic performance of the algorithm can be theoretically predicted by the state evolution, and the measurements entropy estimated by the free entropy formalism. The implementation is modular by design: each module, which implements a factor, can be composed at will with other modules to solve complex inference tasks. The user only needs to declare the factor graph of the model: the inference algorithm, state evolution and entropy estimation are fully automated.
Exact asymptotics for phase retrieval and compressed sensing with random generative priors
Dec 04, 2019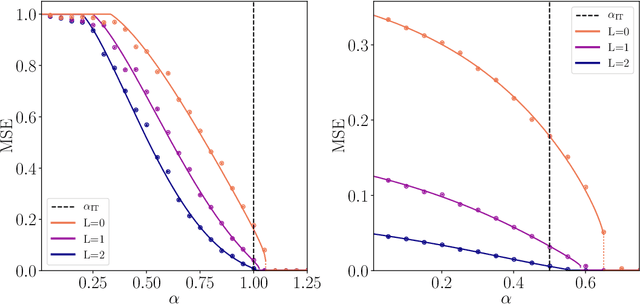
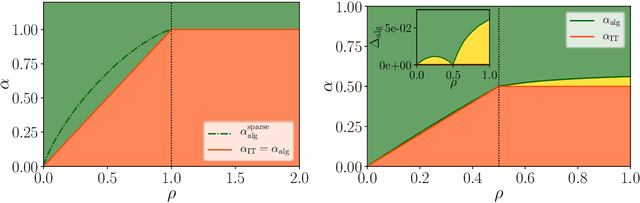
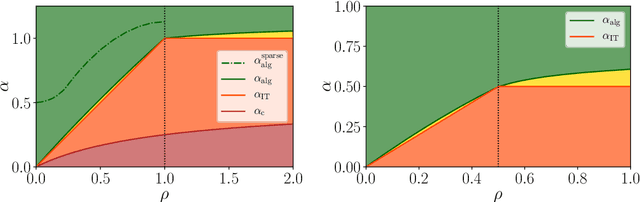
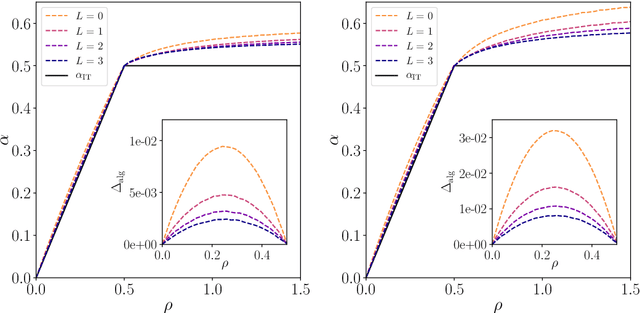
Abstract:We consider the problem of compressed sensing and of (real-valued) phase retrieval with random measurement matrix. We derive sharp asymptotics for the information-theoretically optimal performance and for the best known polynomial algorithm for an ensemble of generative priors consisting of fully connected deep neural networks with random weight matrices and arbitrary activations. We compare the performance to sparse separable priors and conclude that generative priors might be advantageous in terms of algorithmic performance. In particular, while sparsity does not allow to perform compressive phase retrieval efficiently close to its information-theoretic limit, it is found that under the random generative prior compressed phase retrieval becomes tractable.
On the Universality of Noiseless Linear Estimation with Respect to the Measurement Matrix
Jun 11, 2019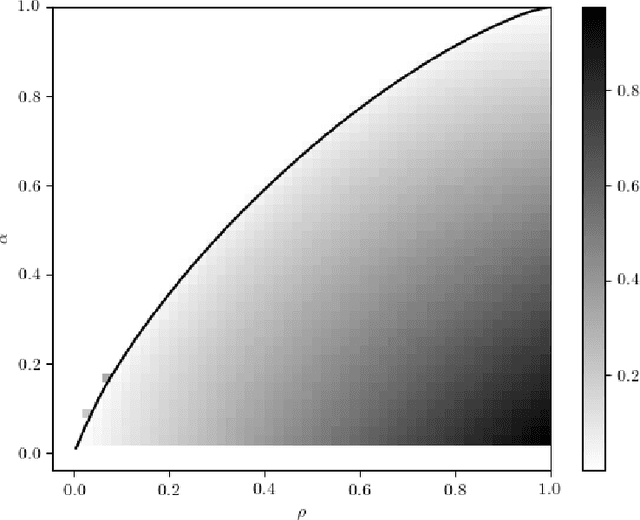
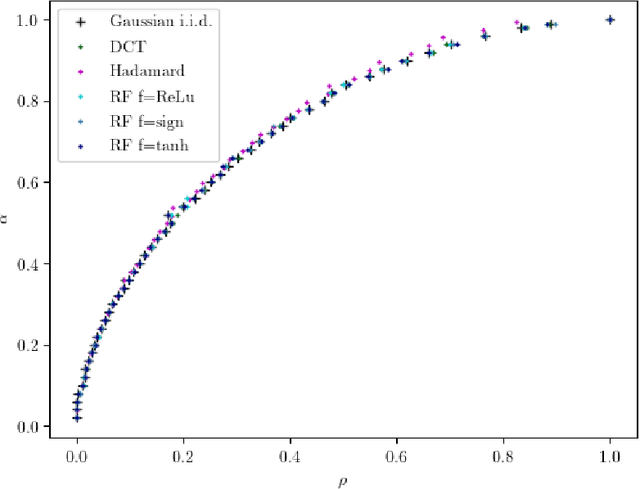
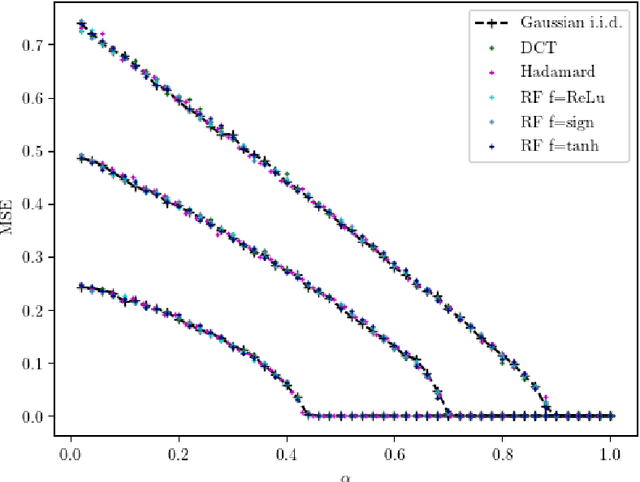
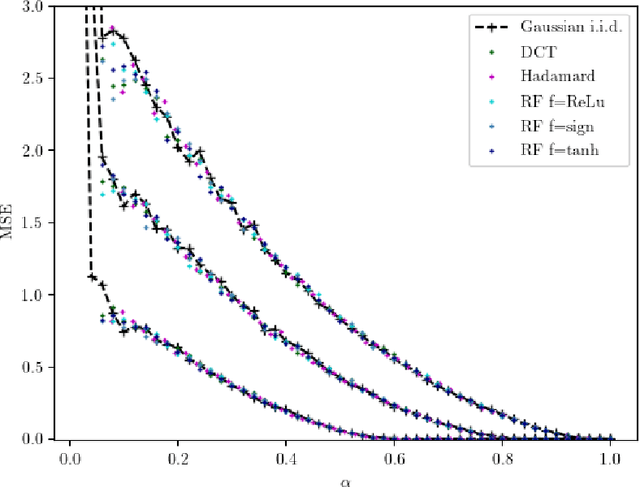
Abstract:In a noiseless linear estimation problem, one aims to reconstruct a vector x* from the knowledge of its linear projections y=Phi x*. There have been many theoretical works concentrating on the case where the matrix Phi is a random i.i.d. one, but a number of heuristic evidence suggests that many of these results are universal and extend well beyond this restricted case. Here we revisit this problematic through the prism of development of message passing methods, and consider not only the universality of the l1 transition, as previously addressed, but also the one of the optimal Bayesian reconstruction. We observed that the universality extends to the Bayes-optimal minimum mean-squared (MMSE) error, and to a range of structured matrices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge