Asymptotics of Non-Convex Generalized Linear Models in High-Dimensions: A proof of the replica formula

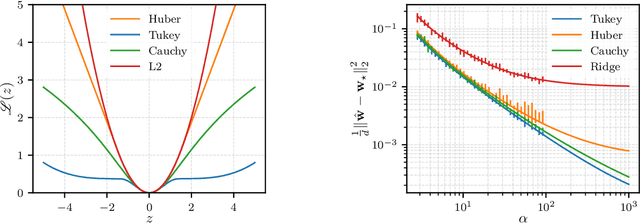
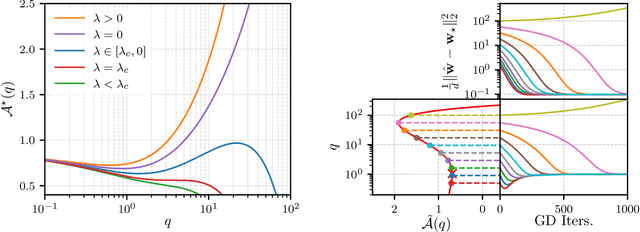
The analytic characterization of the high-dimensional behavior of optimization for Generalized Linear Models (GLMs) with Gaussian data has been a central focus in statistics and probability in recent years. While convex cases, such as the LASSO, ridge regression, and logistic regression, have been extensively studied using a variety of techniques, the non-convex case remains far less understood despite its significance. A non-rigorous statistical physics framework has provided remarkable predictions for the behavior of high-dimensional optimization problems, but rigorously establishing their validity for non-convex problems has remained a fundamental challenge. In this work, we address this challenge by developing a systematic framework that rigorously proves replica-symmetric formulas for non-convex GLMs and precisely determines the conditions under which these formulas are valid. Remarkably, the rigorous replica-symmetric predictions align exactly with the conjectures made by physicists, and the so-called replicon condition. The originality of our approach lies in connecting two powerful theoretical tools: the Gaussian Min-Max Theorem, which we use to provide precise lower bounds, and Approximate Message Passing (AMP), which is shown to achieve these bounds algorithmically. We demonstrate the utility of this framework through significant applications: (i) by proving the optimality of the Tukey loss over the more commonly used Huber loss under a $\varepsilon$ contaminated data model, (ii) establishing the optimality of negative regularization in high-dimensional non-convex regression and (iii) characterizing the performance limits of linearized AMP algorithms. By rigorously validating statistical physics predictions in non-convex settings, we aim to open new pathways for analyzing increasingly complex optimization landscapes beyond the convex regime.

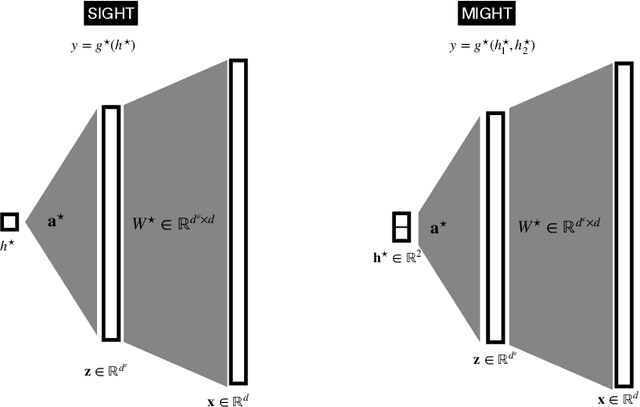
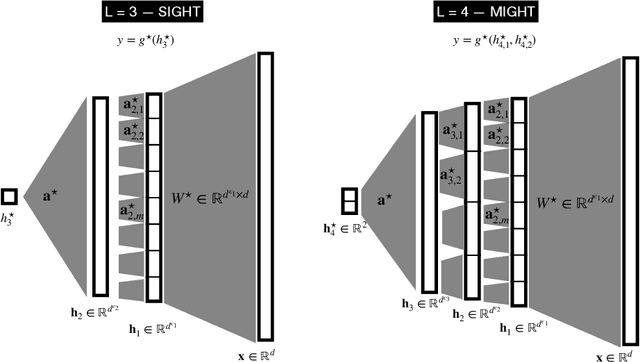
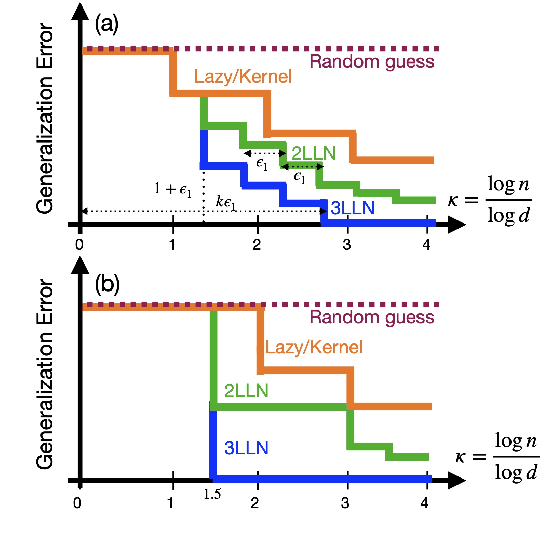
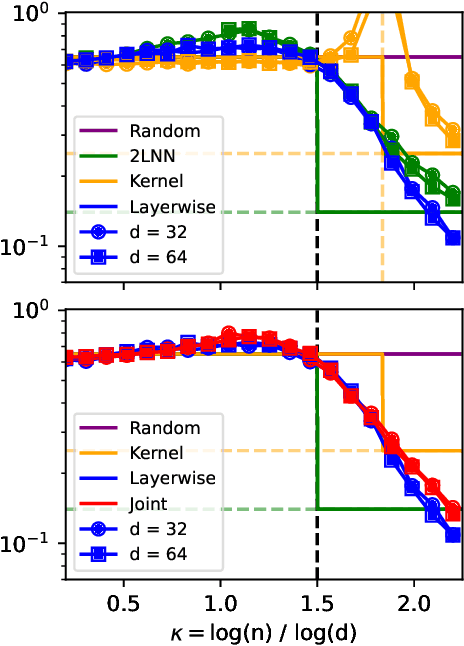
The Computational Advantage of Depth: Learning High-Dimensional Hierarchical Functions with Gradient Descent

Understanding the advantages of deep neural networks trained by gradient descent (GD) compared to shallow models remains an open theoretical challenge. While the study of multi-index models with Gaussian data in high dimensions has provided analytical insights into the benefits of GD-trained neural networks over kernels, the role of depth in improving sample complexity and generalization in GD-trained networks remains poorly understood. In this paper, we introduce a class of target functions (single and multi-index Gaussian hierarchical targets) that incorporate a hierarchy of latent subspace dimensionalities. This framework enables us to analytically study the learning dynamics and generalization performance of deep networks compared to shallow ones in the high-dimensional limit. Specifically, our main theorem shows that feature learning with GD reduces the effective dimensionality, transforming a high-dimensional problem into a sequence of lower-dimensional ones. This enables learning the target function with drastically less samples than with shallow networks. While the results are proven in a controlled training setting, we also discuss more common training procedures and argue that they learn through the same mechanisms. These findings open the way to further quantitative studies of the crucial role of depth in learning hierarchical structures with deep networks.

Optimal Spectral Transitions in High-Dimensional Multi-Index Models

We consider the problem of how many samples from a Gaussian multi-index model are required to weakly reconstruct the relevant index subspace. Despite its increasing popularity as a testbed for investigating the computational complexity of neural networks, results beyond the single-index setting remain elusive. In this work, we introduce spectral algorithms based on the linearization of a message passing scheme tailored to this problem. Our main contribution is to show that the proposed methods achieve the optimal reconstruction threshold. Leveraging a high-dimensional characterization of the algorithms, we show that above the critical threshold the leading eigenvector correlates with the relevant index subspace, a phenomenon reminiscent of the Baik-Ben Arous-Peche (BBP) transition in spiked models arising in random matrix theory. Supported by numerical experiments and a rigorous theoretical framework, our work bridges critical gaps in the computational limits of weak learnability in multi-index model.

Fundamental limits of learning in sequence multi-index models and deep attention networks: High-dimensional asymptotics and sharp thresholds

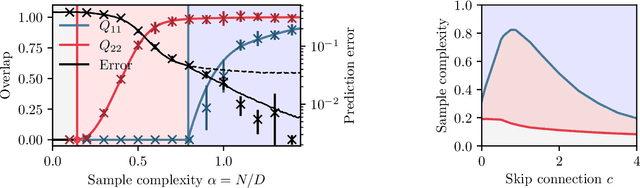
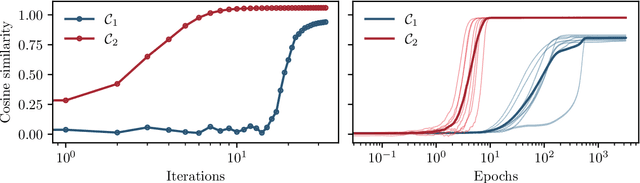
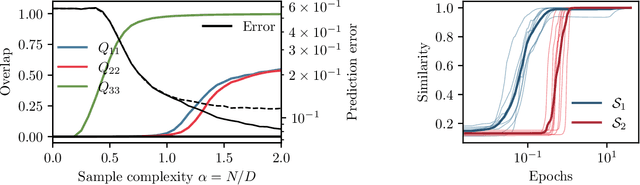
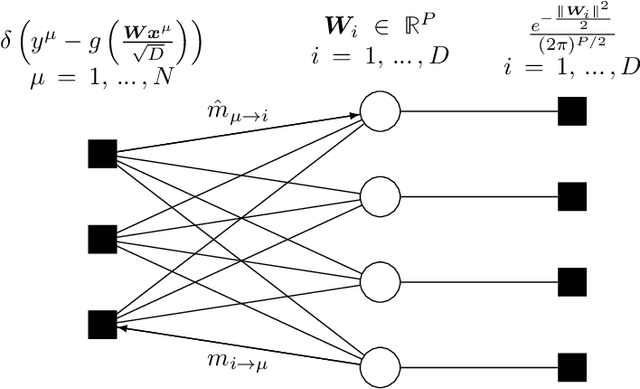
In this manuscript, we study the learning of deep attention neural networks, defined as the composition of multiple self-attention layers, with tied and low-rank weights. We first establish a mapping of such models to sequence multi-index models, a generalization of the widely studied multi-index model to sequential covariates, for which we establish a number of general results. In the context of Bayesian-optimal learning, in the limit of large dimension $D$ and commensurably large number of samples $N$, we derive a sharp asymptotic characterization of the optimal performance as well as the performance of the best-known polynomial-time algorithm for this setting --namely approximate message-passing--, and characterize sharp thresholds on the minimal sample complexity required for better-than-random prediction performance. Our analysis uncovers, in particular, how the different layers are learned sequentially. Finally, we discuss how this sequential learning can also be observed in a realistic setup.

A Random Matrix Theory Perspective on the Spectrum of Learned Features and Asymptotic Generalization Capabilities

A key property of neural networks is their capacity of adapting to data during training. Yet, our current mathematical understanding of feature learning and its relationship to generalization remain limited. In this work, we provide a random matrix analysis of how fully-connected two-layer neural networks adapt to the target function after a single, but aggressive, gradient descent step. We rigorously establish the equivalence between the updated features and an isotropic spiked random feature model, in the limit of large batch size. For the latter model, we derive a deterministic equivalent description of the feature empirical covariance matrix in terms of certain low-dimensional operators. This allows us to sharply characterize the impact of training in the asymptotic feature spectrum, and in particular, provides a theoretical grounding for how the tails of the feature spectrum modify with training. The deterministic equivalent further yields the exact asymptotic generalization error, shedding light on the mechanisms behind its improvement in the presence of feature learning. Our result goes beyond standard random matrix ensembles, and therefore we believe it is of independent technical interest. Different from previous work, our result holds in the challenging maximal learning rate regime, is fully rigorous and allows for finitely supported second layer initialization, which turns out to be crucial for studying the functional expressivity of the learned features. This provides a sharp description of the impact of feature learning in the generalization of two-layer neural networks, beyond the random features and lazy training regimes.

Bayes-optimal learning of an extensive-width neural network from quadratically many samples

We consider the problem of learning a target function corresponding to a single hidden layer neural network, with a quadratic activation function after the first layer, and random weights. We consider the asymptotic limit where the input dimension and the network width are proportionally large. Recent work [Cui & al '23] established that linear regression provides Bayes-optimal test error to learn such a function when the number of available samples is only linear in the dimension. That work stressed the open challenge of theoretically analyzing the optimal test error in the more interesting regime where the number of samples is quadratic in the dimension. In this paper, we solve this challenge for quadratic activations and derive a closed-form expression for the Bayes-optimal test error. We also provide an algorithm, that we call GAMP-RIE, which combines approximate message passing with rotationally invariant matrix denoising, and that asymptotically achieves the optimal performance. Technically, our result is enabled by establishing a link with recent works on optimal denoising of extensive-rank matrices and on the ellipsoid fitting problem. We further show empirically that, in the absence of noise, randomly-initialized gradient descent seems to sample the space of weights, leading to zero training loss, and averaging over initialization leads to a test error equal to the Bayes-optimal one.

Online Learning and Information Exponents: On The Importance of Batch size, and Time/Complexity Tradeoffs

We study the impact of the batch size $n_b$ on the iteration time $T$ of training two-layer neural networks with one-pass stochastic gradient descent (SGD) on multi-index target functions of isotropic covariates. We characterize the optimal batch size minimizing the iteration time as a function of the hardness of the target, as characterized by the information exponents. We show that performing gradient updates with large batches $n_b \lesssim d^{\frac{\ell}{2}}$ minimizes the training time without changing the total sample complexity, where $\ell$ is the information exponent of the target to be learned \citep{arous2021online} and $d$ is the input dimension. However, larger batch sizes than $n_b \gg d^{\frac{\ell}{2}}$ are detrimental for improving the time complexity of SGD. We provably overcome this fundamental limitation via a different training protocol, \textit{Correlation loss SGD}, which suppresses the auto-correlation terms in the loss function. We show that one can track the training progress by a system of low-dimensional ordinary differential equations (ODEs). Finally, we validate our theoretical results with numerical experiments.

Fundamental limits of weak learnability in high-dimensional multi-index models

Multi-index models -- functions which only depend on the covariates through a non-linear transformation of their projection on a subspace -- are a useful benchmark for investigating feature learning with neural networks. This paper examines the theoretical boundaries of learnability in this hypothesis class, focusing particularly on the minimum sample complexity required for weakly recovering their low-dimensional structure with first-order iterative algorithms, in the high-dimensional regime where the number of samples is $n=\alpha d$ is proportional to the covariate dimension $d$. Our findings unfold in three parts: (i) first, we identify under which conditions a \textit{trivial subspace} can be learned with a single step of a first-order algorithm for any $\alpha\!>\!0$; (ii) second, in the case where the trivial subspace is empty, we provide necessary and sufficient conditions for the existence of an {\it easy subspace} consisting of directions that can be learned only above a certain sample complexity $\alpha\!>\!\alpha_c$. The critical threshold $\alpha_{c}$ marks the presence of a computational phase transition, in the sense that no efficient iterative algorithm can succeed for $\alpha\!<\!\alpha_c$. In a limited but interesting set of really hard directions -- akin to the parity problem -- $\alpha_c$ is found to diverge. Finally, (iii) we demonstrate that interactions between different directions can result in an intricate hierarchical learning phenomenon, where some directions can be learned sequentially when coupled to easier ones. Our analytical approach is built on the optimality of approximate message-passing algorithms among first-order iterative methods, delineating the fundamental learnability limit across a broad spectrum of algorithms, including neural networks trained with gradient descent.

Repetita Iuvant: Data Repetition Allows SGD to Learn High-Dimensional Multi-Index Functions

Neural networks can identify low-dimensional relevant structures within high-dimensional noisy data, yet our mathematical understanding of how they do so remains scarce. Here, we investigate the training dynamics of two-layer shallow neural networks trained with gradient-based algorithms, and discuss how they learn pertinent features in multi-index models, that is target functions with low-dimensional relevant directions. In the high-dimensional regime, where the input dimension $d$ diverges, we show that a simple modification of the idealized single-pass gradient descent training scenario, where data can now be repeated or iterated upon twice, drastically improves its computational efficiency. In particular, it surpasses the limitations previously believed to be dictated by the Information and Leap exponents associated with the target function to be learned. Our results highlight the ability of networks to learn relevant structures from data alone without any pre-processing. More precisely, we show that (almost) all directions are learned with at most $O(d \log d)$ steps. Among the exceptions is a set of hard functions that includes sparse parities. In the presence of coupling between directions, however, these can be learned sequentially through a hierarchical mechanism that generalizes the notion of staircase functions. Our results are proven by a rigorous study of the evolution of the relevant statistics for high-dimensional dynamics.

Fundamental limits of Non-Linear Low-Rank Matrix Estimation

We consider the task of estimating a low-rank matrix from non-linear and noisy observations. We prove a strong universality result showing that Bayes-optimal performances are characterized by an equivalent Gaussian model with an effective prior, whose parameters are entirely determined by an expansion of the non-linear function. In particular, we show that to reconstruct the signal accurately, one requires a signal-to-noise ratio growing as $N^{\frac 12 (1-1/k_F)}$, where $k_F$ is the first non-zero Fisher information coefficient of the function. We provide asymptotic characterization for the minimal achievable mean squared error (MMSE) and an approximate message-passing algorithm that reaches the MMSE under conditions analogous to the linear version of the problem. We also provide asymptotic errors achieved by methods such as principal component analysis combined with Bayesian denoising, and compare them with Bayes-optimal MMSE.