Community detection with the Bethe-Hessian

The Bethe-Hessian matrix, introduced by Saade, Krzakala, and Zdeborov\'a (2014), is a Hermitian matrix designed for applying spectral clustering algorithms to sparse networks. Rather than employing a non-symmetric and high-dimensional non-backtracking operator, a spectral method based on the Bethe-Hessian matrix is conjectured to also reach the Kesten-Stigum detection threshold in the sparse stochastic block model (SBM). We provide the first rigorous analysis of the Bethe-Hessian spectral method in the SBM under both the bounded expected degree and the growing degree regimes. Specifically, we demonstrate that: (i) When the expected degree $d\geq 2$, the number of negative outliers of the Bethe-Hessian matrix can consistently estimate the number of blocks above the Kesten-Stigum threshold, thus confirming a conjecture from Saade, Krzakala, and Zdeborov\'a (2014) for $d\geq 2$. (ii) For sufficiently large $d$, its eigenvectors can be used to achieve weak recovery. (iii) As $d\to\infty$, we establish the concentration of the locations of its negative outlier eigenvalues, and weak consistency can be achieved via a spectral method based on the Bethe-Hessian matrix.

Online Learning and Information Exponents: On The Importance of Batch size, and Time/Complexity Tradeoffs

We study the impact of the batch size $n_b$ on the iteration time $T$ of training two-layer neural networks with one-pass stochastic gradient descent (SGD) on multi-index target functions of isotropic covariates. We characterize the optimal batch size minimizing the iteration time as a function of the hardness of the target, as characterized by the information exponents. We show that performing gradient updates with large batches $n_b \lesssim d^{\frac{\ell}{2}}$ minimizes the training time without changing the total sample complexity, where $\ell$ is the information exponent of the target to be learned \citep{arous2021online} and $d$ is the input dimension. However, larger batch sizes than $n_b \gg d^{\frac{\ell}{2}}$ are detrimental for improving the time complexity of SGD. We provably overcome this fundamental limitation via a different training protocol, \textit{Correlation loss SGD}, which suppresses the auto-correlation terms in the loss function. We show that one can track the training progress by a system of low-dimensional ordinary differential equations (ODEs). Finally, we validate our theoretical results with numerical experiments.

Repetita Iuvant: Data Repetition Allows SGD to Learn High-Dimensional Multi-Index Functions

Neural networks can identify low-dimensional relevant structures within high-dimensional noisy data, yet our mathematical understanding of how they do so remains scarce. Here, we investigate the training dynamics of two-layer shallow neural networks trained with gradient-based algorithms, and discuss how they learn pertinent features in multi-index models, that is target functions with low-dimensional relevant directions. In the high-dimensional regime, where the input dimension $d$ diverges, we show that a simple modification of the idealized single-pass gradient descent training scenario, where data can now be repeated or iterated upon twice, drastically improves its computational efficiency. In particular, it surpasses the limitations previously believed to be dictated by the Information and Leap exponents associated with the target function to be learned. Our results highlight the ability of networks to learn relevant structures from data alone without any pre-processing. More precisely, we show that (almost) all directions are learned with at most $O(d \log d)$ steps. Among the exceptions is a set of hard functions that includes sparse parities. In the presence of coupling between directions, however, these can be learned sequentially through a hierarchical mechanism that generalizes the notion of staircase functions. Our results are proven by a rigorous study of the evolution of the relevant statistics for high-dimensional dynamics.

Escaping mediocrity: how two-layer networks learn hard single-index models with SGD

This study explores the sample complexity for two-layer neural networks to learn a single-index target function under Stochastic Gradient Descent (SGD), focusing on the challenging regime where many flat directions are present at initialization. It is well-established that in this scenario $n=O(d\log{d})$ samples are typically needed. However, we provide precise results concerning the pre-factors in high-dimensional contexts and for varying widths. Notably, our findings suggest that overparameterization can only enhance convergence by a constant factor within this problem class. These insights are grounded in the reduction of SGD dynamics to a stochastic process in lower dimensions, where escaping mediocrity equates to calculating an exit time. Yet, we demonstrate that a deterministic approximation of this process adequately represents the escape time, implying that the role of stochasticity may be minimal in this scenario.

Learning Two-Layer Neural Networks, One Step at a Time

We study the training dynamics of shallow neural networks, investigating the conditions under which a limited number of large batch gradient descent steps can facilitate feature learning beyond the kernel regime. We compare the influence of batch size and that of multiple (but finitely many) steps. Our analysis of a single-step process reveals that while a batch size of $n = O(d)$ enables feature learning, it is only adequate for learning a single direction, or a single-index model. In contrast, $n = O(d^2)$ is essential for learning multiple directions and specialization. Moreover, we demonstrate that ``hard'' directions, which lack the first $\ell$ Hermite coefficients, remain unobserved and require a batch size of $n = O(d^\ell)$ for being captured by gradient descent. Upon iterating a few steps, the scenario changes: a batch-size of $n = O(d)$ is enough to learn new target directions spanning the subspace linearly connected in the Hermite basis to the previously learned directions, thereby a staircase property. Our analysis utilizes a blend of techniques related to concentration, projection-based conditioning, and Gaussian equivalence that are of independent interest. By determining the conditions necessary for learning and specialization, our results highlight the interaction between batch size and number of iterations, and lead to a hierarchical depiction where learning performance exhibits a stairway to accuracy over time and batch size, shedding new light on feature learning in neural networks.

Universality laws for Gaussian mixtures in generalized linear models

Let $(x_{i}, y_{i})_{i=1,\dots,n}$ denote independent samples from a general mixture distribution $\sum_{c\in\mathcal{C}}\rho_{c}P_{c}^{x}$, and consider the hypothesis class of generalized linear models $\hat{y} = F(\Theta^{\top}x)$. In this work, we investigate the asymptotic joint statistics of the family of generalized linear estimators $(\Theta_{1}, \dots, \Theta_{M})$ obtained either from (a) minimizing an empirical risk $\hat{R}_{n}(\Theta;X,y)$ or (b) sampling from the associated Gibbs measure $\exp(-\beta n \hat{R}_{n}(\Theta;X,y))$. Our main contribution is to characterize under which conditions the asymptotic joint statistics of this family depends (on a weak sense) only on the means and covariances of the class conditional features distribution $P_{c}^{x}$. In particular, this allow us to prove the universality of different quantities of interest, such as the training and generalization errors, redeeming a recent line of work in high-dimensional statistics working under the Gaussian mixture hypothesis. Finally, we discuss the applications of our results to different machine learning tasks of interest, such as ensembling and uncertainty

Are Gaussian data all you need? Extents and limits of universality in high-dimensional generalized linear estimation

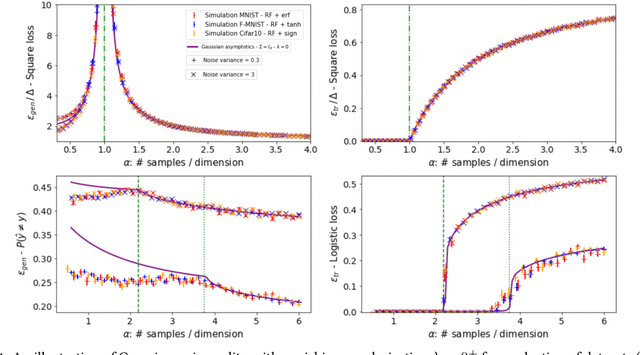
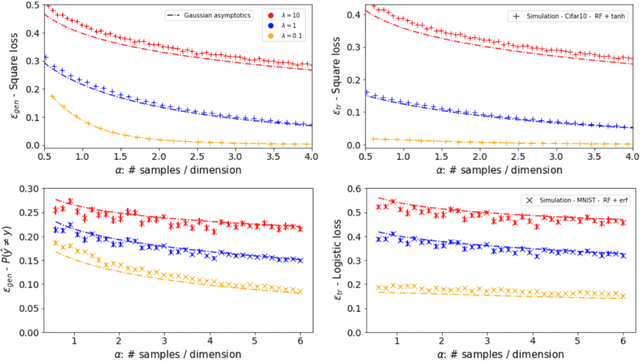
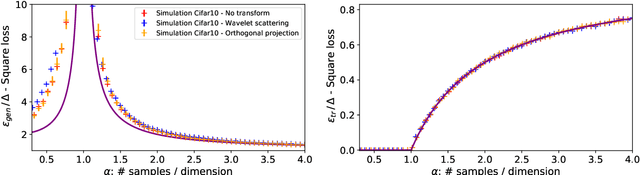
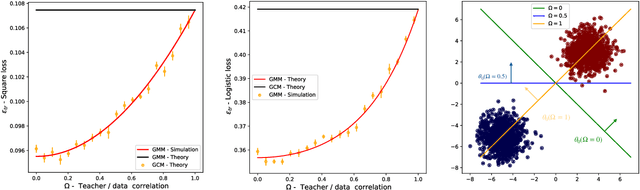
In this manuscript we consider the problem of generalized linear estimation on Gaussian mixture data with labels given by a single-index model. Our first result is a sharp asymptotic expression for the test and training errors in the high-dimensional regime. Motivated by the recent stream of results on the Gaussian universality of the test and training errors in generalized linear estimation, we ask ourselves the question: "when is a single Gaussian enough to characterize the error?". Our formula allow us to give sharp answers to this question, both in the positive and negative directions. More precisely, we show that the sufficient conditions for Gaussian universality (or lack of thereof) crucially depend on the alignment between the target weights and the means and covariances of the mixture clusters, which we precisely quantify. In the particular case of least-squares interpolation, we prove a strong universality property of the training error, and show it follows a simple, closed-form expression. Finally, we apply our results to real datasets, clarifying some recent discussion in the literature about Gaussian universality of the errors in this context.

From high-dimensional & mean-field dynamics to dimensionless ODEs: A unifying approach to SGD in two-layers networks

This manuscript investigates the one-pass stochastic gradient descent (SGD) dynamics of a two-layer neural network trained on Gaussian data and labels generated by a similar, though not necessarily identical, target function. We rigorously analyse the limiting dynamics via a deterministic and low-dimensional description in terms of the sufficient statistics for the population risk. Our unifying analysis bridges different regimes of interest, such as the classical gradient-flow regime of vanishing learning rate, the high-dimensional regime of large input dimension, and the overparameterised "mean-field" regime of large network width, covering as well the intermediate regimes where the limiting dynamics is determined by the interplay between these behaviours. In particular, in the high-dimensional limit, the infinite-width dynamics is found to remain close to a low-dimensional subspace spanned by the target principal directions. Our results therefore provide a unifying picture of the limiting SGD dynamics with synthetic data.

Gaussian Universality of Linear Classifiers with Random Labels in High-Dimension

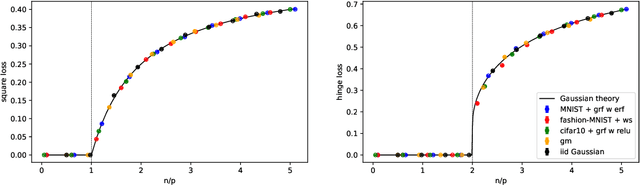
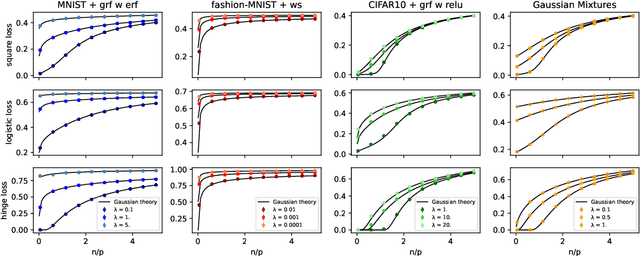
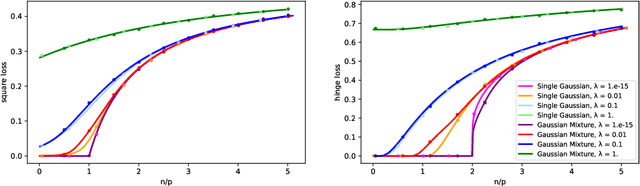
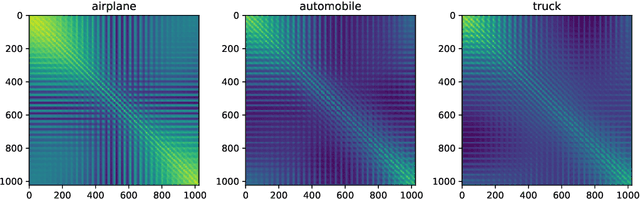
While classical in many theoretical settings, the assumption of Gaussian i.i.d. inputs is often perceived as a strong limitation in the analysis of high-dimensional learning. In this study, we redeem this line of work in the case of generalized linear classification with random labels. Our main contribution is a rigorous proof that data coming from a range of generative models in high-dimensions have the same minimum training loss as Gaussian data with corresponding data covariance. In particular, our theorem covers data created by an arbitrary mixture of homogeneous Gaussian clouds, as well as multi-modal generative neural networks. In the limit of vanishing regularization, we further demonstrate that the training loss is independent of the data covariance. Finally, we show that this universality property is observed in practice with real datasets and random labels.

Sparse random hypergraphs: Non-backtracking spectra and community detection

We consider the community detection problem in a sparse $q$-uniform hypergraph $G$, assuming that $G$ is generated according to the so-called Hypergraph Stochastic Block Model (HSBM). We prove that a spectral method based on the non-backtracking operator for hypergraphs works with high probability down to the generalized Kesten-Stigum detection threshold conjectured by Angelini et al. We characterize the spectrum of the non-backtracking operator for the sparse HSBM, and provide an efficient dimension reduction procedure using the Ihara-Bass formula for hypergraphs. As a result, community detection for the sparse HSBM on $n$ vertices can be reduced to an eigenvector problem of a $2n\times 2n$ non-normal matrix constructed from the adjacency matrix and the degree matrix of the hypergraph. To the best of our knowledge, this is the first provable and efficient spectral algorithm that achieves the conjectured threshold for HSBMs with $k$ blocks generated according to a general symmetric probability tensor.