Yatin Dandi
Asymptotics of Non-Convex Generalized Linear Models in High-Dimensions: A proof of the replica formula
Feb 27, 2025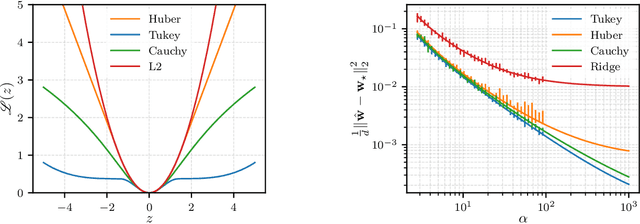
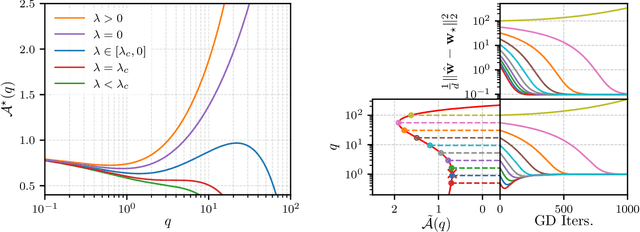
Abstract:The analytic characterization of the high-dimensional behavior of optimization for Generalized Linear Models (GLMs) with Gaussian data has been a central focus in statistics and probability in recent years. While convex cases, such as the LASSO, ridge regression, and logistic regression, have been extensively studied using a variety of techniques, the non-convex case remains far less understood despite its significance. A non-rigorous statistical physics framework has provided remarkable predictions for the behavior of high-dimensional optimization problems, but rigorously establishing their validity for non-convex problems has remained a fundamental challenge. In this work, we address this challenge by developing a systematic framework that rigorously proves replica-symmetric formulas for non-convex GLMs and precisely determines the conditions under which these formulas are valid. Remarkably, the rigorous replica-symmetric predictions align exactly with the conjectures made by physicists, and the so-called replicon condition. The originality of our approach lies in connecting two powerful theoretical tools: the Gaussian Min-Max Theorem, which we use to provide precise lower bounds, and Approximate Message Passing (AMP), which is shown to achieve these bounds algorithmically. We demonstrate the utility of this framework through significant applications: (i) by proving the optimality of the Tukey loss over the more commonly used Huber loss under a $\varepsilon$ contaminated data model, (ii) establishing the optimality of negative regularization in high-dimensional non-convex regression and (iii) characterizing the performance limits of linearized AMP algorithms. By rigorously validating statistical physics predictions in non-convex settings, we aim to open new pathways for analyzing increasingly complex optimization landscapes beyond the convex regime.
The Computational Advantage of Depth: Learning High-Dimensional Hierarchical Functions with Gradient Descent
Feb 19, 2025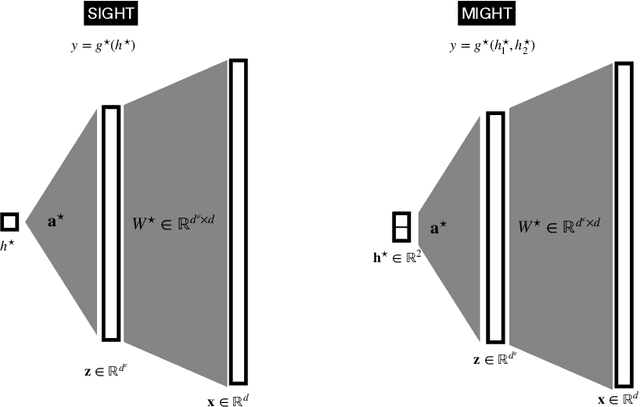
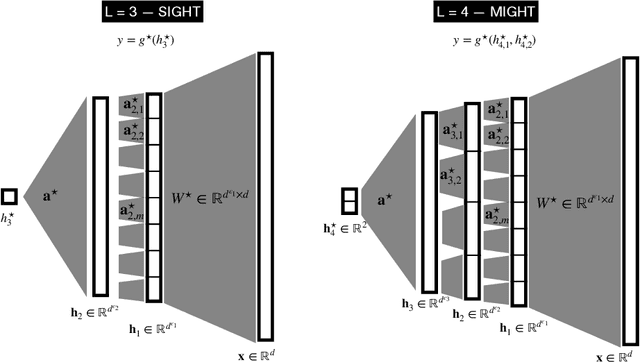
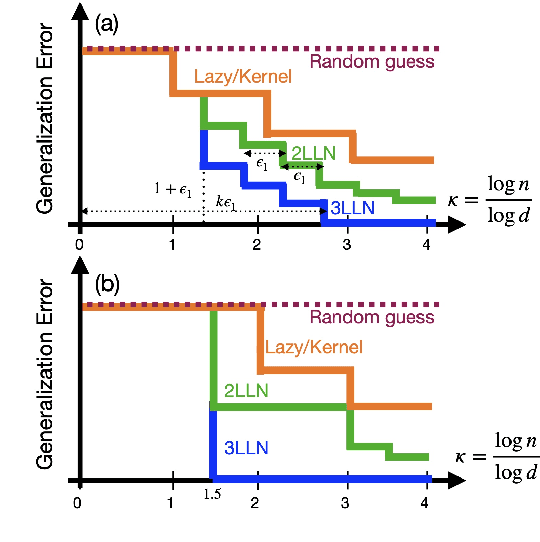
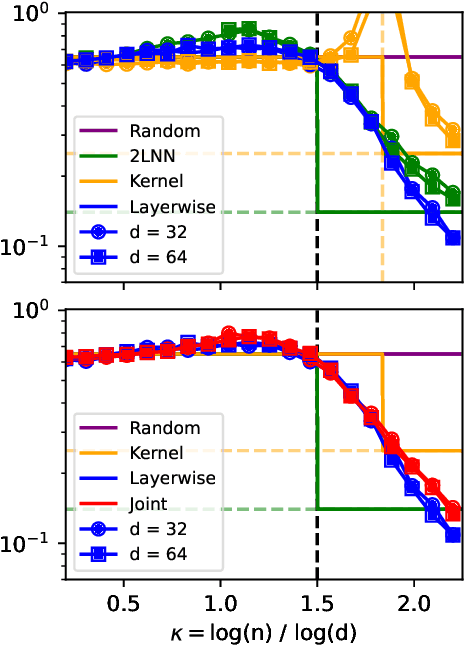
Abstract:Understanding the advantages of deep neural networks trained by gradient descent (GD) compared to shallow models remains an open theoretical challenge. While the study of multi-index models with Gaussian data in high dimensions has provided analytical insights into the benefits of GD-trained neural networks over kernels, the role of depth in improving sample complexity and generalization in GD-trained networks remains poorly understood. In this paper, we introduce a class of target functions (single and multi-index Gaussian hierarchical targets) that incorporate a hierarchy of latent subspace dimensionalities. This framework enables us to analytically study the learning dynamics and generalization performance of deep networks compared to shallow ones in the high-dimensional limit. Specifically, our main theorem shows that feature learning with GD reduces the effective dimensionality, transforming a high-dimensional problem into a sequence of lower-dimensional ones. This enables learning the target function with drastically less samples than with shallow networks. While the results are proven in a controlled training setting, we also discuss more common training procedures and argue that they learn through the same mechanisms. These findings open the way to further quantitative studies of the crucial role of depth in learning hierarchical structures with deep networks.
Optimal Spectral Transitions in High-Dimensional Multi-Index Models
Feb 04, 2025Abstract:We consider the problem of how many samples from a Gaussian multi-index model are required to weakly reconstruct the relevant index subspace. Despite its increasing popularity as a testbed for investigating the computational complexity of neural networks, results beyond the single-index setting remain elusive. In this work, we introduce spectral algorithms based on the linearization of a message passing scheme tailored to this problem. Our main contribution is to show that the proposed methods achieve the optimal reconstruction threshold. Leveraging a high-dimensional characterization of the algorithms, we show that above the critical threshold the leading eigenvector correlates with the relevant index subspace, a phenomenon reminiscent of the Baik-Ben Arous-Peche (BBP) transition in spiked models arising in random matrix theory. Supported by numerical experiments and a rigorous theoretical framework, our work bridges critical gaps in the computational limits of weak learnability in multi-index model.
Fundamental limits of learning in sequence multi-index models and deep attention networks: High-dimensional asymptotics and sharp thresholds
Feb 02, 2025Abstract:In this manuscript, we study the learning of deep attention neural networks, defined as the composition of multiple self-attention layers, with tied and low-rank weights. We first establish a mapping of such models to sequence multi-index models, a generalization of the widely studied multi-index model to sequential covariates, for which we establish a number of general results. In the context of Bayesian-optimal learning, in the limit of large dimension $D$ and commensurably large number of samples $N$, we derive a sharp asymptotic characterization of the optimal performance as well as the performance of the best-known polynomial-time algorithm for this setting --namely approximate message-passing--, and characterize sharp thresholds on the minimal sample complexity required for better-than-random prediction performance. Our analysis uncovers, in particular, how the different layers are learned sequentially. Finally, we discuss how this sequential learning can also be observed in a realistic setup.
A Random Matrix Theory Perspective on the Spectrum of Learned Features and Asymptotic Generalization Capabilities
Oct 24, 2024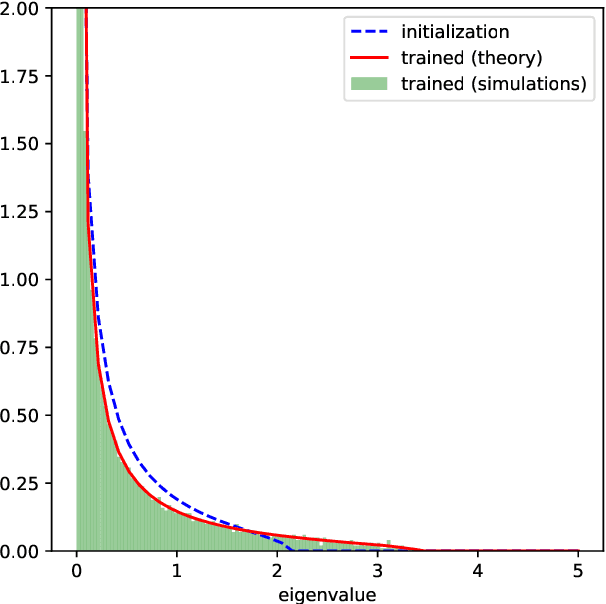
Abstract:A key property of neural networks is their capacity of adapting to data during training. Yet, our current mathematical understanding of feature learning and its relationship to generalization remain limited. In this work, we provide a random matrix analysis of how fully-connected two-layer neural networks adapt to the target function after a single, but aggressive, gradient descent step. We rigorously establish the equivalence between the updated features and an isotropic spiked random feature model, in the limit of large batch size. For the latter model, we derive a deterministic equivalent description of the feature empirical covariance matrix in terms of certain low-dimensional operators. This allows us to sharply characterize the impact of training in the asymptotic feature spectrum, and in particular, provides a theoretical grounding for how the tails of the feature spectrum modify with training. The deterministic equivalent further yields the exact asymptotic generalization error, shedding light on the mechanisms behind its improvement in the presence of feature learning. Our result goes beyond standard random matrix ensembles, and therefore we believe it is of independent technical interest. Different from previous work, our result holds in the challenging maximal learning rate regime, is fully rigorous and allows for finitely supported second layer initialization, which turns out to be crucial for studying the functional expressivity of the learned features. This provides a sharp description of the impact of feature learning in the generalization of two-layer neural networks, beyond the random features and lazy training regimes.
Online Learning and Information Exponents: On The Importance of Batch size, and Time/Complexity Tradeoffs
Jun 04, 2024Abstract:We study the impact of the batch size $n_b$ on the iteration time $T$ of training two-layer neural networks with one-pass stochastic gradient descent (SGD) on multi-index target functions of isotropic covariates. We characterize the optimal batch size minimizing the iteration time as a function of the hardness of the target, as characterized by the information exponents. We show that performing gradient updates with large batches $n_b \lesssim d^{\frac{\ell}{2}}$ minimizes the training time without changing the total sample complexity, where $\ell$ is the information exponent of the target to be learned \citep{arous2021online} and $d$ is the input dimension. However, larger batch sizes than $n_b \gg d^{\frac{\ell}{2}}$ are detrimental for improving the time complexity of SGD. We provably overcome this fundamental limitation via a different training protocol, \textit{Correlation loss SGD}, which suppresses the auto-correlation terms in the loss function. We show that one can track the training progress by a system of low-dimensional ordinary differential equations (ODEs). Finally, we validate our theoretical results with numerical experiments.
Repetita Iuvant: Data Repetition Allows SGD to Learn High-Dimensional Multi-Index Functions
May 24, 2024Abstract:Neural networks can identify low-dimensional relevant structures within high-dimensional noisy data, yet our mathematical understanding of how they do so remains scarce. Here, we investigate the training dynamics of two-layer shallow neural networks trained with gradient-based algorithms, and discuss how they learn pertinent features in multi-index models, that is target functions with low-dimensional relevant directions. In the high-dimensional regime, where the input dimension $d$ diverges, we show that a simple modification of the idealized single-pass gradient descent training scenario, where data can now be repeated or iterated upon twice, drastically improves its computational efficiency. In particular, it surpasses the limitations previously believed to be dictated by the Information and Leap exponents associated with the target function to be learned. Our results highlight the ability of networks to learn relevant structures from data alone without any pre-processing. More precisely, we show that (almost) all directions are learned with at most $O(d \log d)$ steps. Among the exceptions is a set of hard functions that includes sparse parities. In the presence of coupling between directions, however, these can be learned sequentially through a hierarchical mechanism that generalizes the notion of staircase functions. Our results are proven by a rigorous study of the evolution of the relevant statistics for high-dimensional dynamics.
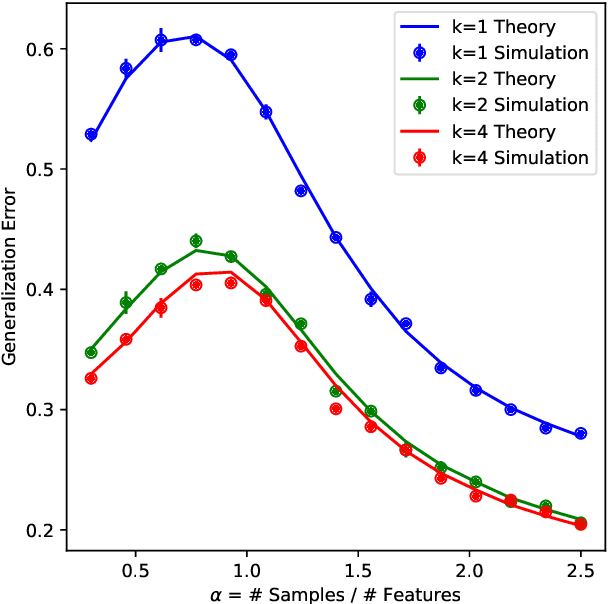
Fundamental limits of weak learnability in high-dimensional multi-index models
May 24, 2024Abstract:Multi-index models -- functions which only depend on the covariates through a non-linear transformation of their projection on a subspace -- are a useful benchmark for investigating feature learning with neural networks. This paper examines the theoretical boundaries of learnability in this hypothesis class, focusing particularly on the minimum sample complexity required for weakly recovering their low-dimensional structure with first-order iterative algorithms, in the high-dimensional regime where the number of samples is $n=\alpha d$ is proportional to the covariate dimension $d$. Our findings unfold in three parts: (i) first, we identify under which conditions a \textit{trivial subspace} can be learned with a single step of a first-order algorithm for any $\alpha\!>\!0$; (ii) second, in the case where the trivial subspace is empty, we provide necessary and sufficient conditions for the existence of an {\it easy subspace} consisting of directions that can be learned only above a certain sample complexity $\alpha\!>\!\alpha_c$. The critical threshold $\alpha_{c}$ marks the presence of a computational phase transition, in the sense that no efficient iterative algorithm can succeed for $\alpha\!<\!\alpha_c$. In a limited but interesting set of really hard directions -- akin to the parity problem -- $\alpha_c$ is found to diverge. Finally, (iii) we demonstrate that interactions between different directions can result in an intricate hierarchical learning phenomenon, where some directions can be learned sequentially when coupled to easier ones. Our analytical approach is built on the optimality of approximate message-passing algorithms among first-order iterative methods, delineating the fundamental learnability limit across a broad spectrum of algorithms, including neural networks trained with gradient descent.
Asymptotics of feature learning in two-layer networks after one gradient-step
Feb 07, 2024Abstract:In this manuscript we investigate the problem of how two-layer neural networks learn features from data, and improve over the kernel regime, after being trained with a single gradient descent step. Leveraging a connection from (Ba et al., 2022) with a non-linear spiked matrix model and recent progress on Gaussian universality (Dandi et al., 2023), we provide an exact asymptotic description of the generalization error in the high-dimensional limit where the number of samples $n$, the width $p$ and the input dimension $d$ grow at a proportional rate. We characterize exactly how adapting to the data is crucial for the network to efficiently learn non-linear functions in the direction of the gradient -- where at initialization it can only express linear functions in this regime. To our knowledge, our results provides the first tight description of the impact of feature learning in the generalization of two-layer neural networks in the large learning rate regime $\eta=\Theta_{d}(d)$, beyond perturbative finite width corrections of the conjugate and neural tangent kernels.
The Benefits of Reusing Batches for Gradient Descent in Two-Layer Networks: Breaking the Curse of Information and Leap Exponents
Feb 05, 2024

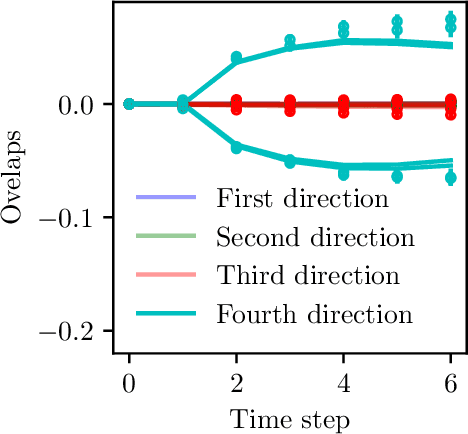
Abstract:We investigate the training dynamics of two-layer neural networks when learning multi-index target functions. We focus on multi-pass gradient descent (GD) that reuses the batches multiple times and show that it significantly changes the conclusion about which functions are learnable compared to single-pass gradient descent. In particular, multi-pass GD with finite stepsize is found to overcome the limitations of gradient flow and single-pass GD given by the information exponent (Ben Arous et al., 2021) and leap exponent (Abbe et al., 2023) of the target function. We show that upon re-using batches, the network achieves in just two time steps an overlap with the target subspace even for functions not satisfying the staircase property (Abbe et al., 2021). We characterize the (broad) class of functions efficiently learned in finite time. The proof of our results is based on the analysis of the Dynamical Mean-Field Theory (DMFT). We further provide a closed-form description of the dynamical process of the low-dimensional projections of the weights, and numerical experiments illustrating the theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge