Asymptotics of Non-Convex Generalized Linear Models in High-Dimensions: A proof of the replica formula

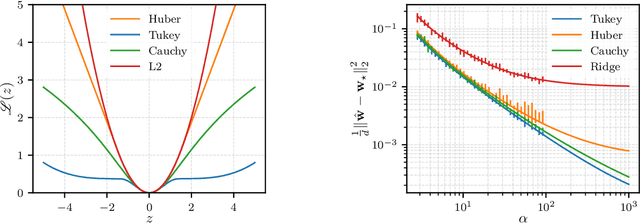
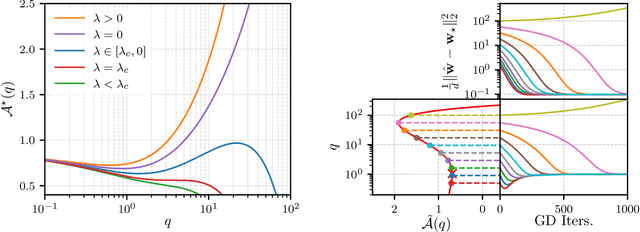
The analytic characterization of the high-dimensional behavior of optimization for Generalized Linear Models (GLMs) with Gaussian data has been a central focus in statistics and probability in recent years. While convex cases, such as the LASSO, ridge regression, and logistic regression, have been extensively studied using a variety of techniques, the non-convex case remains far less understood despite its significance. A non-rigorous statistical physics framework has provided remarkable predictions for the behavior of high-dimensional optimization problems, but rigorously establishing their validity for non-convex problems has remained a fundamental challenge. In this work, we address this challenge by developing a systematic framework that rigorously proves replica-symmetric formulas for non-convex GLMs and precisely determines the conditions under which these formulas are valid. Remarkably, the rigorous replica-symmetric predictions align exactly with the conjectures made by physicists, and the so-called replicon condition. The originality of our approach lies in connecting two powerful theoretical tools: the Gaussian Min-Max Theorem, which we use to provide precise lower bounds, and Approximate Message Passing (AMP), which is shown to achieve these bounds algorithmically. We demonstrate the utility of this framework through significant applications: (i) by proving the optimality of the Tukey loss over the more commonly used Huber loss under a $\varepsilon$ contaminated data model, (ii) establishing the optimality of negative regularization in high-dimensional non-convex regression and (iii) characterizing the performance limits of linearized AMP algorithms. By rigorously validating statistical physics predictions in non-convex settings, we aim to open new pathways for analyzing increasingly complex optimization landscapes beyond the convex regime.

Rigorous dynamical mean field theory for stochastic gradient descent methods

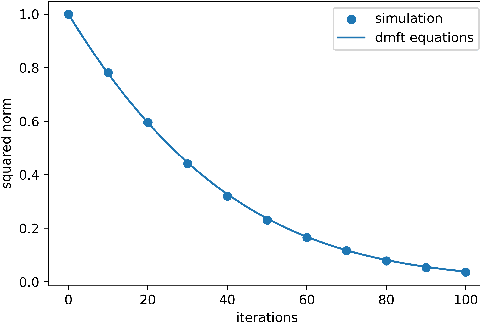
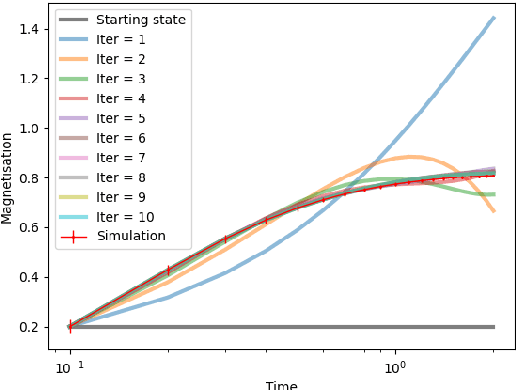
We prove closed-form equations for the exact high-dimensional asymptotics of a family of first order gradient-based methods, learning an estimator (e.g. M-estimator, shallow neural network, ...) from observations on Gaussian data with empirical risk minimization. This includes widely used algorithms such as stochastic gradient descent (SGD) or Nesterov acceleration. The obtained equations match those resulting from the discretization of dynamical mean-field theory (DMFT) equations from statistical physics when applied to gradient flow. Our proof method allows us to give an explicit description of how memory kernels build up in the effective dynamics, and to include non-separable update functions, allowing datasets with non-identity covariance matrices. Finally, we provide numerical implementations of the equations for SGD with generic extensive batch-size and with constant learning rates.

Asymptotic Errors for Teacher-Student Convex Generalized Linear Models (or : How to Prove Kabashima's Replica Formula)

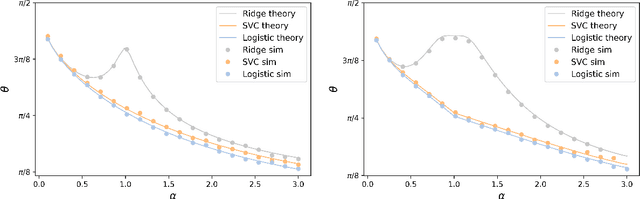
There has been a recent surge of interest in the study of asymptotic reconstruction performance in various cases of generalized linear estimation problems in the teacher-student setting, especially for the case of i.i.d standard normal matrices. In this work, we prove a general analytical formula for the reconstruction performance of convex generalized linear models, and go beyond such matrices by considering all rotationally-invariant data matrices with arbitrary bounded spectrum, proving a decade-old conjecture originally derived using the replica method from statistical physics. This is achieved by leveraging on state-of-the-art advances in message passing algorithms and the statistical properties of their iterates. Our proof is crucially based on the construction of converging sequences of an oracle multi-layer vector approximate message passing algorithm, where the convergence analysis is done by checking the stability of an equivalent dynamical system. Beyond its generality, our result also provides further insight into overparametrized non-linear models, a fundamental building block of modern machine learning. We illustrate our claim with numerical examples on mainstream learning methods such as logistic regression and linear support vector classifiers, showing excellent agreement between moderate size simulation and the asymptotic prediction.