Asymptotic Errors for Teacher-Student Convex Generalized Linear Models (or : How to Prove Kabashima's Replica Formula)

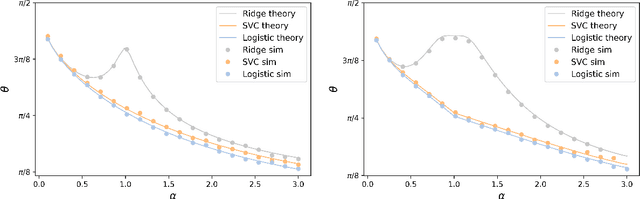
There has been a recent surge of interest in the study of asymptotic reconstruction performance in various cases of generalized linear estimation problems in the teacher-student setting, especially for the case of i.i.d standard normal matrices. In this work, we prove a general analytical formula for the reconstruction performance of convex generalized linear models, and go beyond such matrices by considering all rotationally-invariant data matrices with arbitrary bounded spectrum, proving a decade-old conjecture originally derived using the replica method from statistical physics. This is achieved by leveraging on state-of-the-art advances in message passing algorithms and the statistical properties of their iterates. Our proof is crucially based on the construction of converging sequences of an oracle multi-layer vector approximate message passing algorithm, where the convergence analysis is done by checking the stability of an equivalent dynamical system. Beyond its generality, our result also provides further insight into overparametrized non-linear models, a fundamental building block of modern machine learning. We illustrate our claim with numerical examples on mainstream learning methods such as logistic regression and linear support vector classifiers, showing excellent agreement between moderate size simulation and the asymptotic prediction.