Alia Abbara
Asymptotic Errors for Teacher-Student Convex Generalized Linear Models (or : How to Prove Kabashima's Replica Formula)
Jul 01, 2020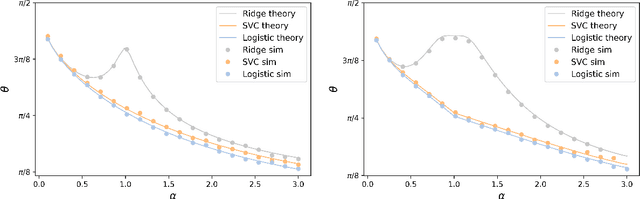
Abstract:There has been a recent surge of interest in the study of asymptotic reconstruction performance in various cases of generalized linear estimation problems in the teacher-student setting, especially for the case of i.i.d standard normal matrices. In this work, we prove a general analytical formula for the reconstruction performance of convex generalized linear models, and go beyond such matrices by considering all rotationally-invariant data matrices with arbitrary bounded spectrum, proving a decade-old conjecture originally derived using the replica method from statistical physics. This is achieved by leveraging on state-of-the-art advances in message passing algorithms and the statistical properties of their iterates. Our proof is crucially based on the construction of converging sequences of an oracle multi-layer vector approximate message passing algorithm, where the convergence analysis is done by checking the stability of an equivalent dynamical system. Beyond its generality, our result also provides further insight into overparametrized non-linear models, a fundamental building block of modern machine learning. We illustrate our claim with numerical examples on mainstream learning methods such as logistic regression and linear support vector classifiers, showing excellent agreement between moderate size simulation and the asymptotic prediction.
Asymptotic errors for convex penalized linear regression beyond Gaussian matrices
Feb 11, 2020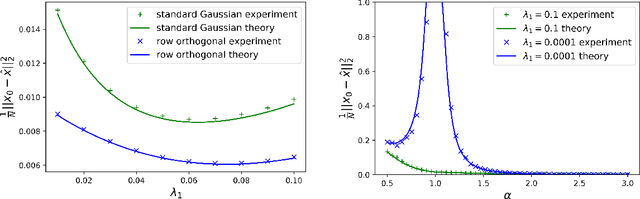
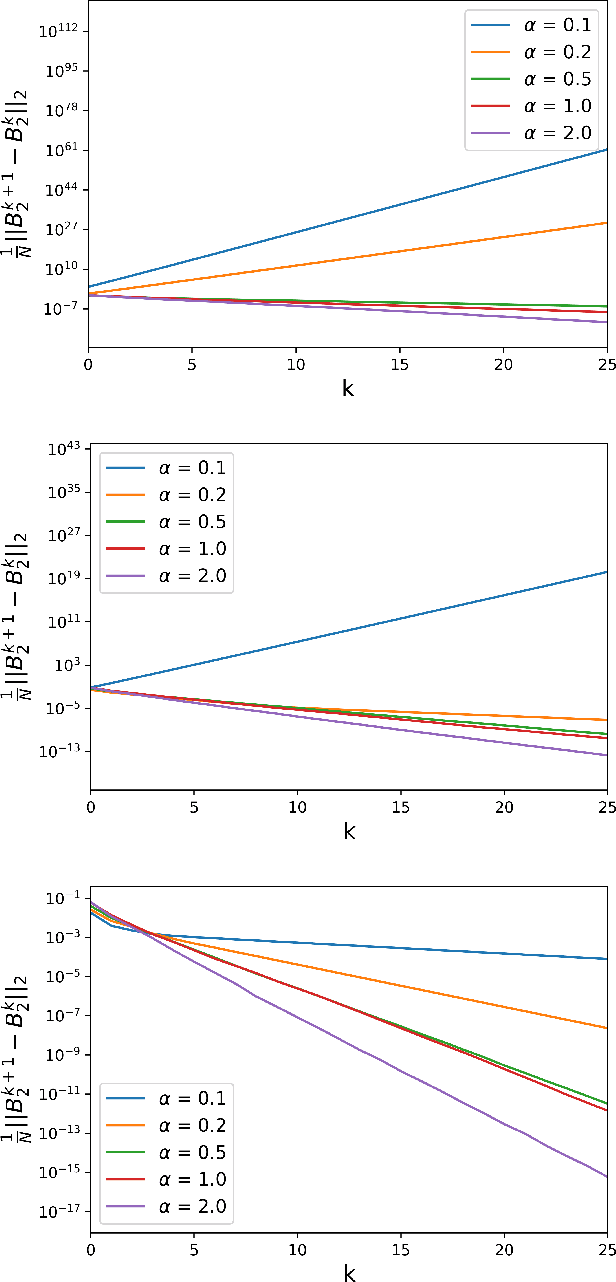
Abstract:We consider the problem of learning a coefficient vector $x_{0}$ in $R^{N}$ from noisy linear observations $y=Fx_{0}+w$ in $R^{M}$ in the high dimensional limit $M,N$ to infinity with $\alpha=M/N$ fixed. We provide a rigorous derivation of an explicit formula -- first conjectured using heuristic methods from statistical physics -- for the asymptotic mean squared error obtained by penalized convex regression estimators such as the LASSO or the elastic net, for a class of very generic random matrices corresponding to rotationally invariant data matrices with arbitrary spectrum. The proof is based on a convergence analysis of an oracle version of vector approximate message-passing (oracle-VAMP) and on the properties of its state evolution equations. Our method leverages on and highlights the link between vector approximate message-passing, Douglas-Rachford splitting and proximal descent algorithms, extending previous results obtained with i.i.d. matrices for a large class of problems. We illustrate our results on some concrete examples and show that even though they are asymptotic, our predictions agree remarkably well with numerics even for very moderate sizes.
Learning performance in inverse Ising problems with sparse teacher couplings
Dec 25, 2019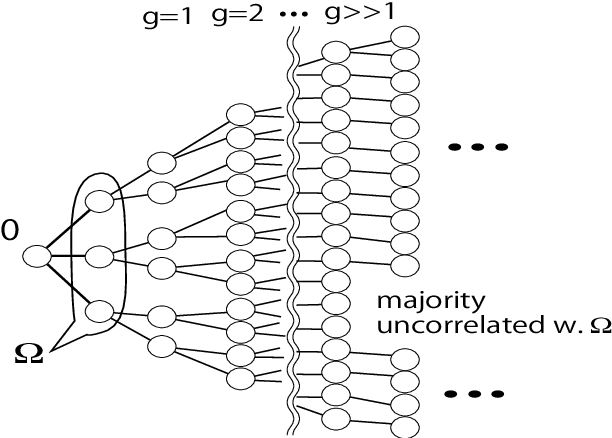
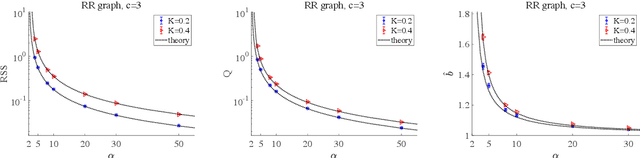
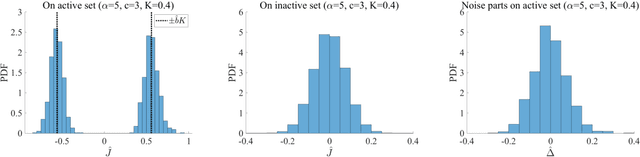
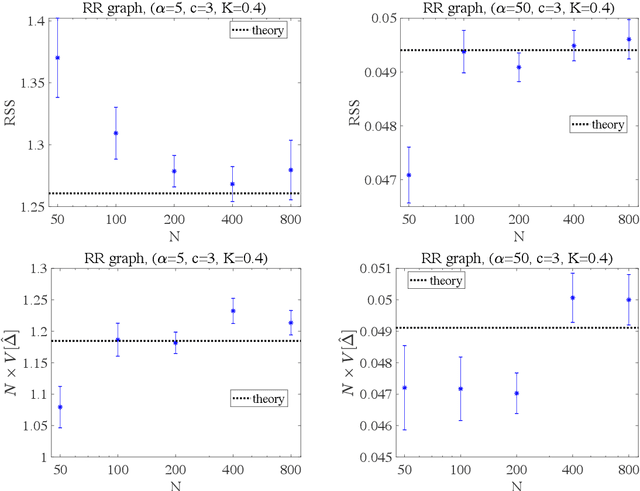
Abstract:We investigate the learning performance of the pseudolikelihood maximization method for inverse Ising problems. In the teacher-student scenario under the assumption that the teacher's couplings are sparse and the student does not know the graphical structure, the learning curve and order parameters are assessed in the typical case using the replica and cavity methods from statistical mechanics. Our formulation is also applicable to a certain class of cost functions having locality; the standard likelihood does not belong to that class. The derived analytical formulas indicate that the perfect inference of the presence/absence of the teacher's couplings is possible in the thermodynamic limit taking the number of spins $N$ as infinity while keeping the dataset size $M$ proportional to $N$, as long as $\alpha=M/N > 2$. Meanwhile, the formulas also show that the estimated coupling values corresponding to the truly existing ones in the teacher tend to be overestimated in the absolute value, manifesting the presence of estimation bias. These results are considered to be exact in the thermodynamic limit on locally tree-like networks, such as the regular random or Erd\H{o}s--R\'enyi graphs. Numerical simulation results fully support the theoretical predictions. Additional biases in the estimators on loopy graphs are also discussed.
Rademacher complexity and spin glasses: A link between the replica and statistical theories of learning
Dec 05, 2019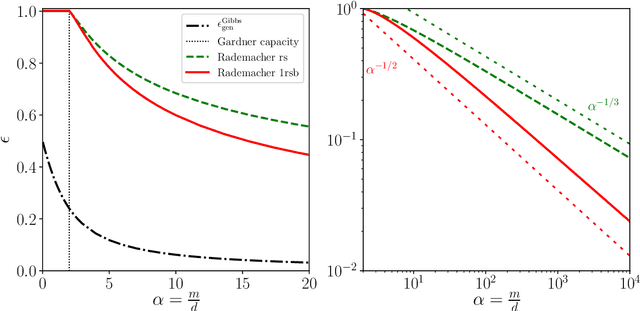
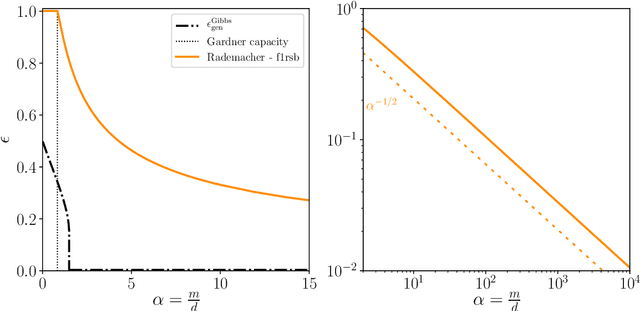
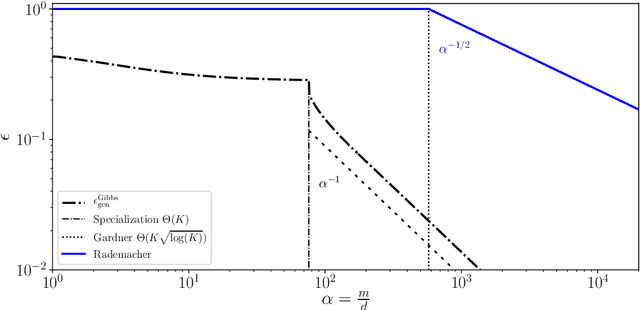
Abstract:Statistical learning theory provides bounds of the generalization gap, using in particular the Vapnik-Chervonenkis dimension and the Rademacher complexity. An alternative approach, mainly studied in the statistical physics literature, is the study of generalization in simple synthetic-data models. Here we discuss the connections between these approaches and focus on the link between the Rademacher complexity in statistical learning and the theories of generalization for typical-case synthetic models from statistical physics, involving quantities known as Gardner capacity and ground state energy. We show that in these models the Rademacher complexity is closely related to the ground state energy computed by replica theories. Using this connection, one may reinterpret many results of the literature as rigorous Rademacher bounds in a variety of models in the high-dimensional statistics limit. Somewhat surprisingly, we also show that statistical learning theory provides predictions for the behavior of the ground-state energies in some full replica symmetry breaking models.
On the Universality of Noiseless Linear Estimation with Respect to the Measurement Matrix
Jun 11, 2019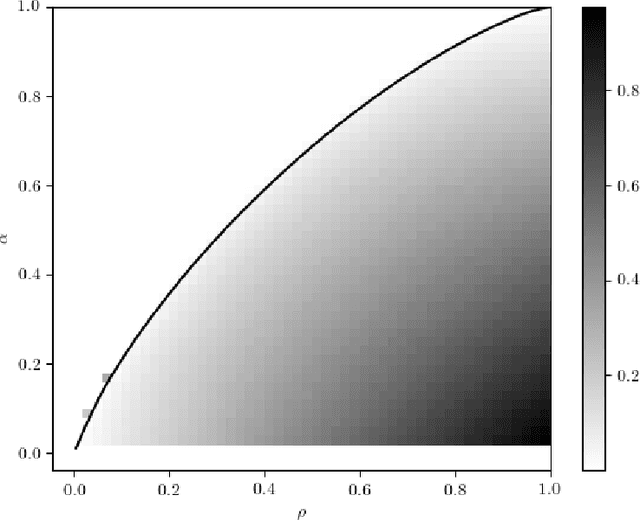
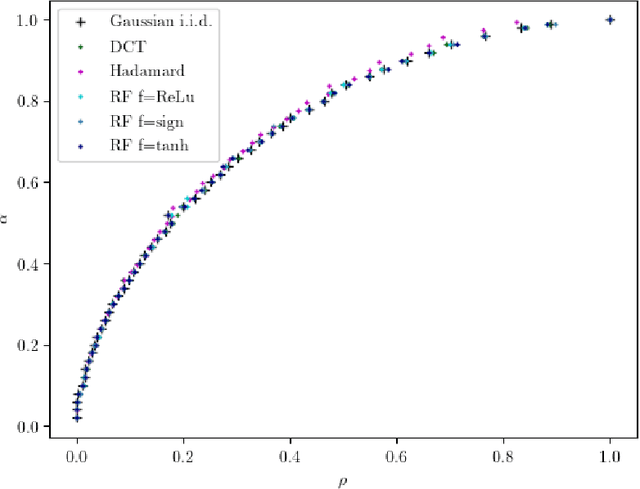
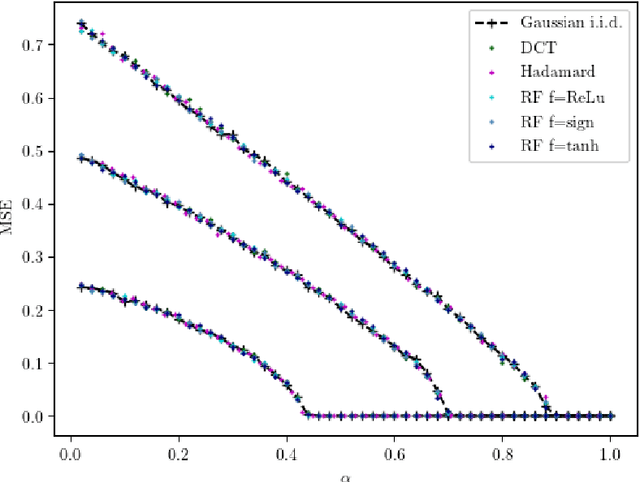
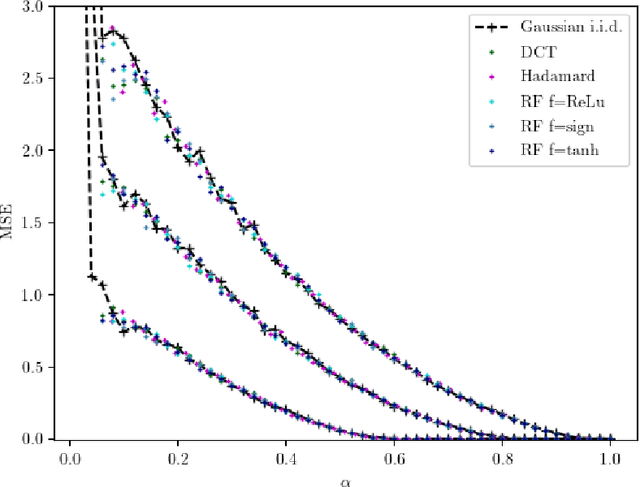
Abstract:In a noiseless linear estimation problem, one aims to reconstruct a vector x* from the knowledge of its linear projections y=Phi x*. There have been many theoretical works concentrating on the case where the matrix Phi is a random i.i.d. one, but a number of heuristic evidence suggests that many of these results are universal and extend well beyond this restricted case. Here we revisit this problematic through the prism of development of message passing methods, and consider not only the universality of the l1 transition, as previously addressed, but also the one of the optimal Bayesian reconstruction. We observed that the universality extends to the Bayes-optimal minimum mean-squared (MMSE) error, and to a range of structured matrices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge