Analysis of High-dimensional Gaussian Labeled-unlabeled Mixture Model via Message-passing Algorithm

Semi-supervised learning (SSL) is a machine learning methodology that leverages unlabeled data in conjunction with a limited amount of labeled data. Although SSL has been applied in various applications and its effectiveness has been empirically demonstrated, it is still not fully understood when and why SSL performs well. Some existing theoretical studies have attempted to address this issue by modeling classification problems using the so-called Gaussian Mixture Model (GMM). These studies provide notable and insightful interpretations. However, their analyses are focused on specific purposes, and a thorough investigation of the properties of GMM in the context of SSL has been lacking. In this paper, we conduct such a detailed analysis of the properties of the high-dimensional GMM for binary classification in the SSL setting. To this end, we employ the approximate message passing and state evolution methods, which are widely used in high-dimensional settings and originate from statistical mechanics. We deal with two estimation approaches: the Bayesian one and the l2-regularized maximum likelihood estimation (RMLE). We conduct a comprehensive comparison between these two approaches, examining aspects such as the global phase diagram, estimation error for the parameters, and prediction error for the labels. A specific comparison is made between the Bayes-optimal (BO) estimator and RMLE, as the BO setting provides optimal estimation performance and is ideal as a benchmark. Our analysis shows that with appropriate regularizations, RMLE can achieve near-optimal performance in terms of both the estimation error and prediction error, especially when there is a large amount of unlabeled data. These results demonstrate that the l2 regularization term plays an effective role in estimation and prediction in SSL approaches.

Transfer Learning in $\ell_1$ Regularized Regression: Hyperparameter Selection Strategy based on Sharp Asymptotic Analysis

Transfer learning techniques aim to leverage information from multiple related datasets to enhance prediction quality against a target dataset. Such methods have been adopted in the context of high-dimensional sparse regression, and some Lasso-based algorithms have been invented: Trans-Lasso and Pretraining Lasso are such examples. These algorithms require the statistician to select hyperparameters that control the extent and type of information transfer from related datasets. However, selection strategies for these hyperparameters, as well as the impact of these choices on the algorithm's performance, have been largely unexplored. To address this, we conduct a thorough, precise study of the algorithm in a high-dimensional setting via an asymptotic analysis using the replica method. Our approach reveals a surprisingly simple behavior of the algorithm: Ignoring one of the two types of information transferred to the fine-tuning stage has little effect on generalization performance, implying that efforts for hyperparameter selection can be significantly reduced. Our theoretical findings are also empirically supported by real-world applications on the IMDb dataset.

When resampling/reweighting improves feature learning in imbalanced classification?: A toy-model study

A toy model of binary classification is studied with the aim of clarifying the class-wise resampling/reweighting effect on the feature learning performance under the presence of class imbalance. In the analysis, a high-dimensional limit of the feature is taken while keeping the dataset size ratio against the feature dimension finite and the non-rigorous replica method from statistical mechanics is employed. The result shows that there exists a case in which the no resampling/reweighting situation gives the best feature learning performance irrespectively of the choice of losses or classifiers, supporting recent findings in Cao et al. (2019); Kang et al. (2019). It is also revealed that the key of the result is the symmetry of the loss and the problem setting. Inspired by this, we propose a further simplified model exhibiting the same property for the multiclass setting. These clarify when the class-wise resampling/reweighting becomes effective in imbalanced classification.

On Model Selection Consistency of Lasso for High-Dimensional Ising Models on Tree-like Graphs

We consider the problem of high-dimensional Ising model selection using neighborhood-based least absolute shrinkage and selection operator (Lasso). It is rigorously proved that under some mild coherence conditions on the population covariance matrix of the Ising model, consistent model selection can be achieved with sample sizes $n=\Omega{(d^3\log{p})}$ for any tree-like graph in the paramagnetic phase, where $p$ is the number of variables and $d$ is the maximum node degree. When the same conditions are imposed directly on the sample covariance matrices, it is shown that a reduced sample size $n=\Omega{(d^2\log{p})}$ suffices. The obtained sufficient conditions for consistent model selection with Lasso are the same in the scaling of the sample complexity as that of $\ell_1$-regularized logistic regression. Given the popularity and efficiency of Lasso, our rigorous analysis provides a theoretical backing for its practical use in Ising model selection.

Ising Model Selection Using $\ell_{1}$-Regularized Linear Regression

We theoretically investigate the performance of $\ell_{1}$-regularized linear regression ($\ell_1$-LinR) for the problem of Ising model selection using the replica method from statistical mechanics. The regular random graph is considered under paramagnetic assumption. Our results show that despite model misspecification, the $\ell_1$-LinR estimator can successfully recover the graph structure of the Ising model with $N$ variables using $M=\mathcal{O}\left(\log N\right)$ samples, which is of the same order as that of $\ell_{1}$-regularized logistic regression. Moreover, we provide a computationally efficient method to accurately predict the non-asymptotic performance of the $\ell_1$-LinR estimator with moderate $M$ and $N$. Simulations show an excellent agreement between theoretical predictions and experimental results, which supports our findings.

Perfect Reconstruction of Sparse Signals via Greedy Monte-Carlo Search

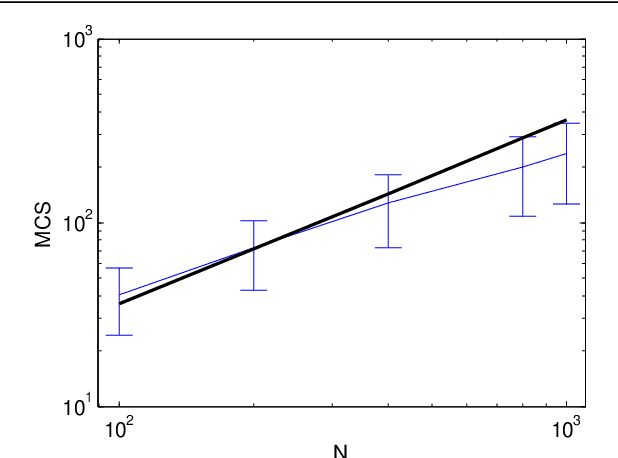
We propose a Monte-Carlo-based method for reconstructing sparse signals in the formulation of sparse linear regression in a high-dimensional setting. The basic idea of this algorithm is to explicitly select variables or covariates to represent a given data vector or responses and accept randomly generated updates of that selection if and only if the energy or cost function decreases. This algorithm is called the greedy Monte-Carlo (GMC) search algorithm. Its performance is examined via numerical experiments, which suggests that in the noiseless case, GMC can achieve perfect reconstruction in undersampling situations of a reasonable level: it can outperform the $\ell_1$ relaxation but does not reach the algorithmic limit of MC-based methods theoretically clarified by an earlier analysis. Additionally, an experiment on a real-world dataset supports the practicality of GMC.

Structure Learning in Inverse Ising Problems Using $\ell_2$-Regularized Linear Estimator

Inferring interaction parameters from observed data is a ubiquitous requirement in various fields of science and engineering. Recent studies have shown that the pseudolikelihood (PL) method is highly effective in meeting this requirement even though the maximum likelihood method is computationally intractable when used directly. To the best of our knowledge, most existing studies assume that the postulated model used in the inference stage covers the true model that generates the data. However, such an assumption does not necessarily hold in practical situations. From this perspective, we discuss the utility of the PL method in model mismatch cases. Specifically, we examine the inference performance of the PL method when $\ell_2$-regularized (ridge) linear regression is applied to data generated from sparse Boltzmann machines of Ising spins using methods of statistical mechanics. Our analysis indicates that despite the model mismatch, one can perfectly identify the network topology using naive linear regression without regularization when the dataset size $M$ is greater than the number of Ising spins, $N$. Further, even when $M < N$, perfect identification is possible using a two-stage estimator with much better quantitative performance compared to naive usage of the PL method. Results of extensive numerical experiments support our findings.

Learning performance in inverse Ising problems with sparse teacher couplings

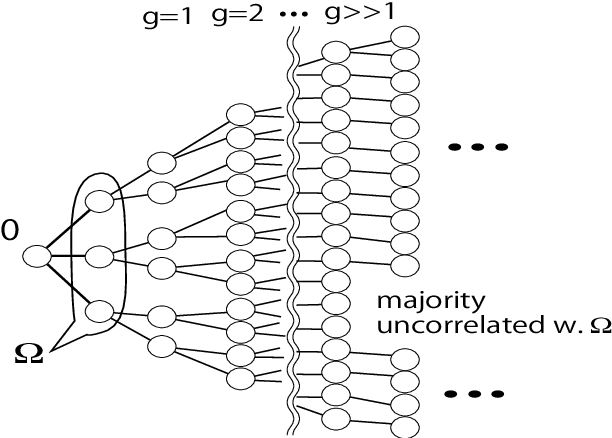
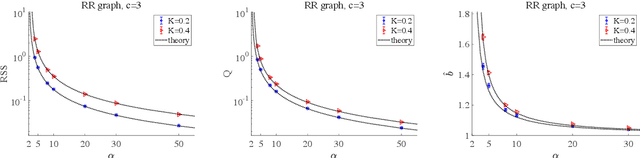
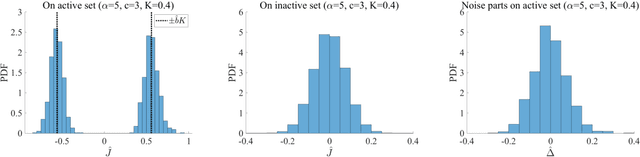
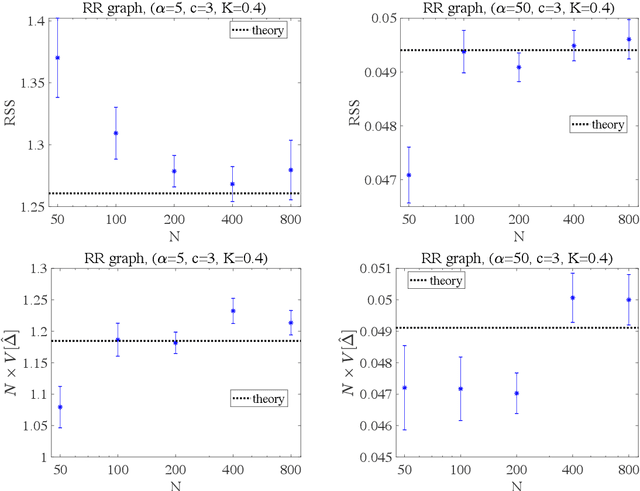
We investigate the learning performance of the pseudolikelihood maximization method for inverse Ising problems. In the teacher-student scenario under the assumption that the teacher's couplings are sparse and the student does not know the graphical structure, the learning curve and order parameters are assessed in the typical case using the replica and cavity methods from statistical mechanics. Our formulation is also applicable to a certain class of cost functions having locality; the standard likelihood does not belong to that class. The derived analytical formulas indicate that the perfect inference of the presence/absence of the teacher's couplings is possible in the thermodynamic limit taking the number of spins $N$ as infinity while keeping the dataset size $M$ proportional to $N$, as long as $\alpha=M/N > 2$. Meanwhile, the formulas also show that the estimated coupling values corresponding to the truly existing ones in the teacher tend to be overestimated in the absolute value, manifesting the presence of estimation bias. These results are considered to be exact in the thermodynamic limit on locally tree-like networks, such as the regular random or Erd\H{o}s--R\'enyi graphs. Numerical simulation results fully support the theoretical predictions. Additional biases in the estimators on loopy graphs are also discussed.

Empirical Bayes Method for Boltzmann Machines

In this study, we consider an empirical Bayes method for Boltzmann machines and propose an algorithm for it. The empirical Bayes method allows estimation of the values of the hyperparameters of the Boltzmann machine by maximizing a specific likelihood function referred to as the empirical Bayes likelihood function in this study. However, the maximization is computationally hard because the empirical Bayes likelihood function involves intractable integrations of the partition function. The proposed algorithm avoids this computational problem by using the replica method and the Plefka expansion. Our method does not require any iterative procedures and is quite simple and fast, though it introduces a bias to the estimate, which exhibits an unnatural behavior with respect to the size of the dataset. This peculiar behavior is supposed to be due to the approximate treatment by the Plefka expansion. A possible extension to overcome this behavior is also discussed.

Cross validation in sparse linear regression with piecewise continuous nonconvex penalties and its acceleration

We investigate the signal reconstruction performance of sparse linear regression in the presence of noise when piecewise continuous nonconvex penalties are used. Among such penalties, we focus on the smoothly clipped absolute deviation (SCAD) penalty. The contributions of this study are three-fold: We first present a theoretical analysis of a typical reconstruction performance, using the replica method, under the assumption that each component of the design matrix is given as an independent and identically distributed (i.i.d.) Gaussian variable. This clarifies the superiority of the SCAD estimator compared with $\ell_1$ in a wide parameter range, although the nonconvex nature of the penalty tends to lead to solution multiplicity in certain regions. This multiplicity is shown to be connected to replica symmetry breaking in the spin-glass theory, and associated phase diagrams are given. We also show that the global minimum of the mean square error between the estimator and the true signal is located in the replica symmetric phase. Second, we develop an approximate formula efficiently computing the cross-validation error without actually conducting the cross-validation, which is also applicable to the non-i.i.d. design matrices. It is shown that this formula is only applicable to the unique solution region and tends to be unstable in the multiple solution region. We implement instability detection procedures, which allows the approximate formula to stand alone and resultantly enables us to draw phase diagrams for any specific dataset. Third, we propose an annealing procedure, called nonconvexity annealing, to obtain the solution path efficiently. Numerical simulations are conducted on simulated datasets to examine these results to verify the consistency of the theoretical results and the efficiency of the approximate formula and nonconvexity annealing.