Neural Collapse in Cumulative Link Models for Ordinal Regression: An Analysis with Unconstrained Feature Model

A phenomenon known as ''Neural Collapse (NC)'' in deep classification tasks, in which the penultimate-layer features and the final classifiers exhibit an extremely simple geometric structure, has recently attracted considerable attention, with the expectation that it can deepen our understanding of how deep neural networks behave. The Unconstrained Feature Model (UFM) has been proposed to explain NC theoretically, and there emerges a growing body of work that extends NC to tasks other than classification and leverages it for practical applications. In this study, we investigate whether a similar phenomenon arises in deep Ordinal Regression (OR) tasks, via combining the cumulative link model for OR and UFM. We show that a phenomenon we call Ordinal Neural Collapse (ONC) indeed emerges and is characterized by the following three properties: (ONC1) all optimal features in the same class collapse to their within-class mean when regularization is applied; (ONC2) these class means align with the classifier, meaning that they collapse onto a one-dimensional subspace; (ONC3) the optimal latent variables (corresponding to logits or preactivations in classification tasks) are aligned according to the class order, and in particular, in the zero-regularization limit, a highly local and simple geometric relationship emerges between the latent variables and the threshold values. We prove these properties analytically within the UFM framework with fixed threshold values and corroborate them empirically across a variety of datasets. We also discuss how these insights can be leveraged in OR, highlighting the use of fixed thresholds.

When resampling/reweighting improves feature learning in imbalanced classification?: A toy-model study

A toy model of binary classification is studied with the aim of clarifying the class-wise resampling/reweighting effect on the feature learning performance under the presence of class imbalance. In the analysis, a high-dimensional limit of the feature is taken while keeping the dataset size ratio against the feature dimension finite and the non-rigorous replica method from statistical mechanics is employed. The result shows that there exists a case in which the no resampling/reweighting situation gives the best feature learning performance irrespectively of the choice of losses or classifiers, supporting recent findings in Cao et al. (2019); Kang et al. (2019). It is also revealed that the key of the result is the symmetry of the loss and the problem setting. Inspired by this, we propose a further simplified model exhibiting the same property for the multiclass setting. These clarify when the class-wise resampling/reweighting becomes effective in imbalanced classification.

Harmonizing Attention: Training-free Texture-aware Geometry Transfer

Extracting geometry features from photographic images independently of surface texture and transferring them onto different materials remains a complex challenge. In this study, we introduce Harmonizing Attention, a novel training-free approach that leverages diffusion models for texture-aware geometry transfer. Our method employs a simple yet effective modification of self-attention layers, allowing the model to query information from multiple reference images within these layers. This mechanism is seamlessly integrated into the inversion process as Texture-aligning Attention and into the generation process as Geometry-aligning Attention. This dual-attention approach ensures the effective capture and transfer of material-independent geometry features while maintaining material-specific textural continuity, all without the need for model fine-tuning.

Remarks on Loss Function of Threshold Method for Ordinal Regression Problem

Threshold methods are popular for ordinal regression problems, which are classification problems for data with a natural ordinal relation. They learn a one-dimensional transformation (1DT) of observations of the explanatory variable, and then assign label predictions to the observations by thresholding their 1DT values. In this paper, we study the influence of the underlying data distribution and of the learning procedure of the 1DT on the classification performance of the threshold method via theoretical considerations and numerical experiments. Consequently, for example, we found that threshold methods based on typical learning procedures may perform poorly when the probability distribution of the target variable conditioned on an observation of the explanatory variable tends to be non-unimodal. Another instance of our findings is that learned 1DT values are concentrated at a few points under the learning procedure based on a piecewise-linear loss function, which can make difficult to classify data well.

Parallel Algorithm for Optimal Threshold Labeling of Ordinal Regression Methods

Ordinal regression (OR) is classification of ordinal data in which the underlying categorical target variable has a natural ordinal relation for the underlying explanatory variable. For $K$-class OR tasks, threshold methods learn a one-dimensional transformation (1DT) of the explanatory variable so that 1DT values for observations of the explanatory variable preserve the order of label values $1,\ldots,K$ for corresponding observations of the target variable well, and then assign a label prediction to the learned 1DT through threshold labeling, namely, according to the rank of an interval to which the 1DT belongs among intervals on the real line separated by $(K-1)$ threshold parameters. In this study, we propose a parallelizable algorithm to find the optimal threshold labeling, which was developed in previous research, and derive sufficient conditions for that algorithm to successfully output the optimal threshold labeling. In a numerical experiment we performed, the computation time taken for the whole learning process of a threshold method with the optimal threshold labeling could be reduced to approximately 60\,\% by using the proposed algorithm with parallel processing compared to using an existing algorithm based on dynamic programming.

Universality of reservoir systems with recurrent neural networks

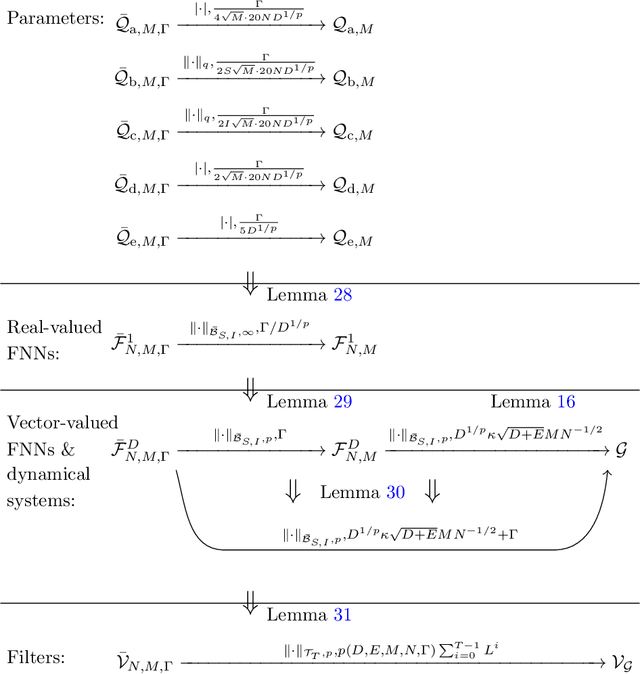
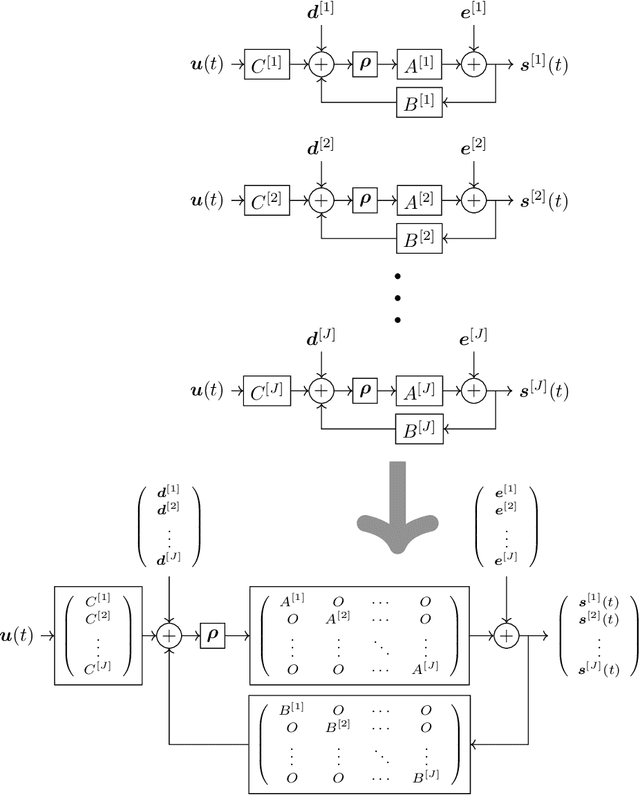
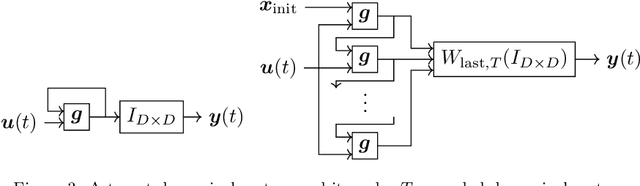
Approximation capability of reservoir systems whose reservoir is a recurrent neural network (RNN) is discussed. In our problem setting, a reservoir system approximates a set of functions just by adjusting its linear readout while the reservoir is fixed. We will show what we call uniform strong universality of a family of RNN reservoir systems for a certain class of functions to be approximated. This means that, for any positive number, we can construct a sufficiently large RNN reservoir system whose approximation error for each function in the class of functions to be approximated is bounded from above by the positive number. Such RNN reservoir systems are constructed via parallel concatenation of RNN reservoirs.

Spatio-temporal reconstruction of substance dynamics using compressed sensing in multi-spectral magnetic resonance spectroscopic imaging

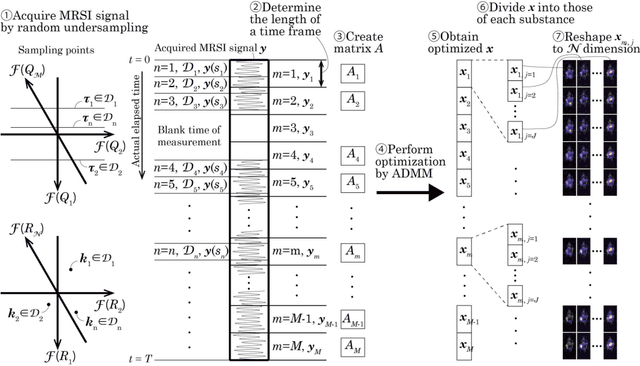
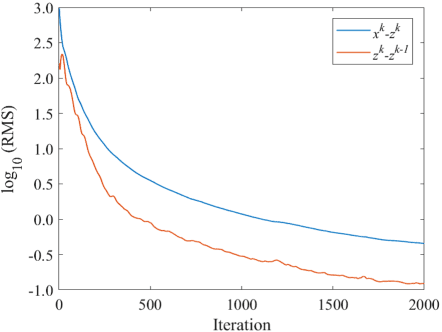
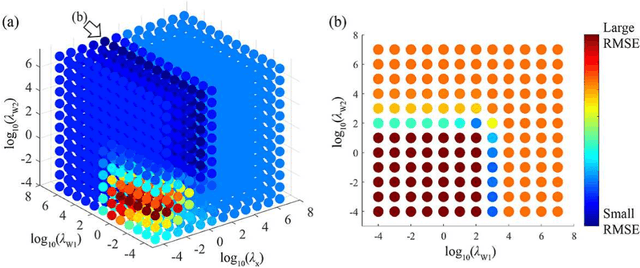
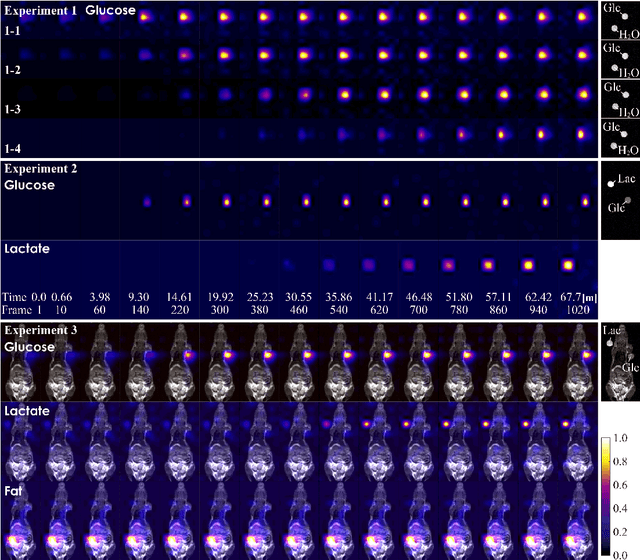
The objective of our study is to observe dynamics of multiple substances in vivo with high temporal resolution from multi-spectral magnetic resonance spectroscopic imaging (MRSI) data. The multi-spectral MRSI can effectively separate spectral peaks of multiple substances and is useful to measure spatial distributions of substances. However it is difficult to measure time-varying substance distributions directly by ordinary full sampling because the measurement requires a significantly long time. In this study, we propose a novel method to reconstruct the spatio-temporal distributions of substances from randomly undersampled multi-spectral MRSI data on the basis of compressed sensing (CS) and the partially separable function model with base spectra of substances. In our method, we have employed spatio-temporal sparsity and temporal smoothness of the substance distributions as prior knowledge to perform CS. The effectiveness of our method has been evaluated using phantom data sets of glass tubes filled with glucose or lactate solution in increasing amounts over time and animal data sets of a tumor-bearing mouse to observe the metabolic dynamics involved in the Warburg effect in vivo. The reconstructed results are consistent with the expected behaviors, showing that our method can reconstruct the spatio-temporal distribution of substances with a temporal resolution of four seconds which is extremely short time scale compared with that of full sampling. Since this method utilizes only prior knowledge naturally assumed for the spatio-temporal distributions of substances and is independent of the number of the spectral and spatial dimensions or the acquisition sequence of MRSI, it is expected to contribute to revealing the underlying substance dynamics in MRSI data already acquired or to be acquired in the future.

Convergence Analysis of Blurring Mean Shift

Blurring mean shift (BMS) algorithm, a variant of the mean shift algorithm, is a kernel-based iterative method for data clustering, where data points are clustered according to their convergent points via iterative blurring. In this paper, we analyze convergence properties of the BMS algorithm by leveraging its interpretation as an optimization procedure, which is known but has been underutilized in existing convergence studies. Whereas existing results on convergence properties applicable to multi-dimensional data only cover the case where all the blurred data point sequences converge to a single point, this study provides a convergence guarantee even when those sequences can converge to multiple points, yielding multiple clusters. This study also shows that the convergence of the BMS algorithm is fast by further leveraging geometrical characterization of the convergent points.

Negative-prompt Inversion: Fast Image Inversion for Editing with Text-guided Diffusion Models

In image editing employing diffusion models, it is crucial to preserve the reconstruction quality of the original image while changing its style. Although existing methods ensure reconstruction quality through optimization, a drawback of these is the significant amount of time required for optimization. In this paper, we propose negative-prompt inversion, a method capable of achieving equivalent reconstruction solely through forward propagation without optimization, thereby enabling much faster editing processes. We experimentally demonstrate that the reconstruction quality of our method is comparable to that of existing methods, allowing for inversion at a resolution of 512 pixels and with 50 sampling steps within approximately 5 seconds, which is more than 30 times faster than null-text inversion. Reduction of the computation time by the proposed method further allows us to use a larger number of sampling steps in diffusion models to improve the reconstruction quality with a moderate increase in computation time.

Convergence Analysis of Mean Shift

The mean shift (MS) algorithm seeks a mode of the kernel density estimate (KDE). This study presents a convergence guarantee of the mode estimate sequence generated by the MS algorithm and an evaluation of the convergence rate, under fairly mild conditions, with the help of the argument concerning the {\L}ojasiewicz inequality. Our findings, which extend existing ones covering analytic kernels and the Epanechnikov kernel, are significant in that they cover the biweight kernel that is optimal among non-negative kernels in terms of the asymptotic statistical efficiency for the KDE-based mode estimation.