Universality of reservoir systems with recurrent neural networks
Paper and Code
Mar 04, 2024
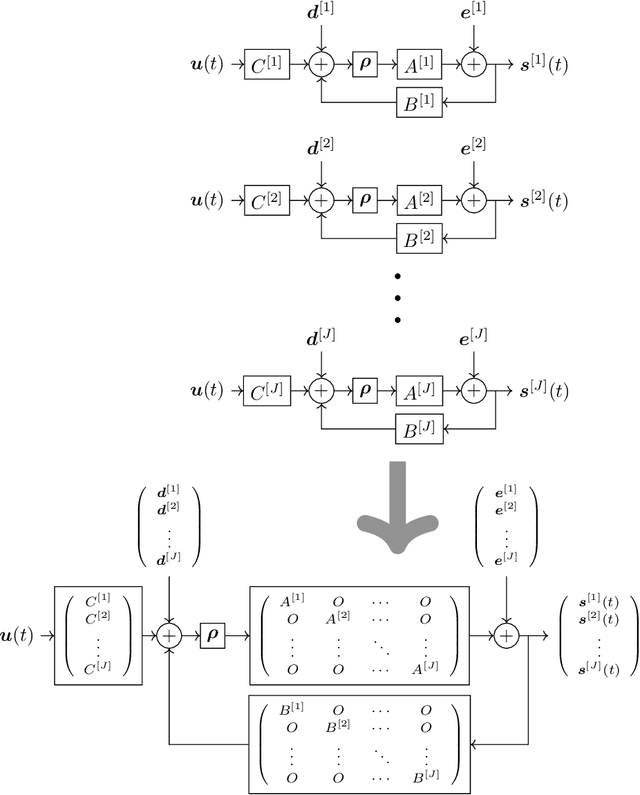
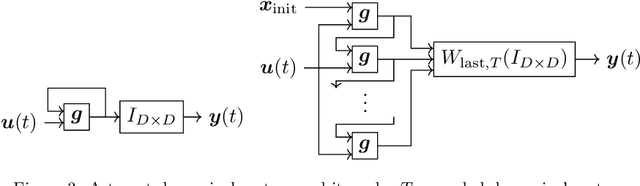
Approximation capability of reservoir systems whose reservoir is a recurrent neural network (RNN) is discussed. In our problem setting, a reservoir system approximates a set of functions just by adjusting its linear readout while the reservoir is fixed. We will show what we call uniform strong universality of a family of RNN reservoir systems for a certain class of functions to be approximated. This means that, for any positive number, we can construct a sufficiently large RNN reservoir system whose approximation error for each function in the class of functions to be approximated is bounded from above by the positive number. Such RNN reservoir systems are constructed via parallel concatenation of RNN reservoirs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge