Spatio-temporal reconstruction of substance dynamics using compressed sensing in multi-spectral magnetic resonance spectroscopic imaging

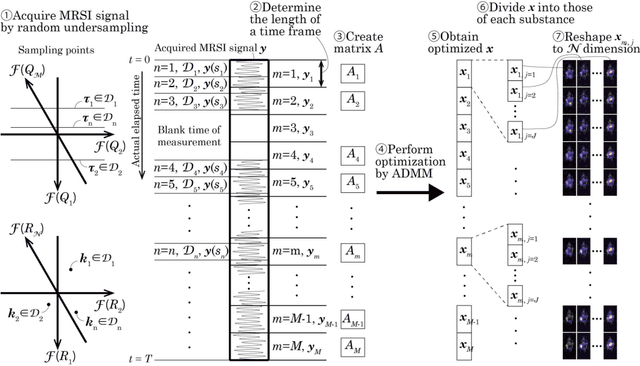
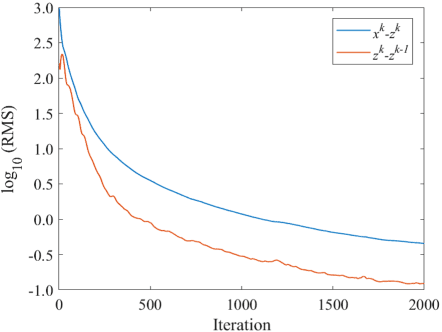
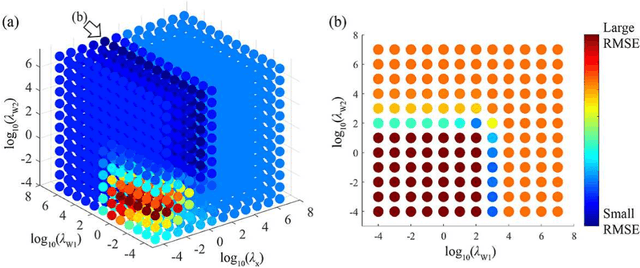
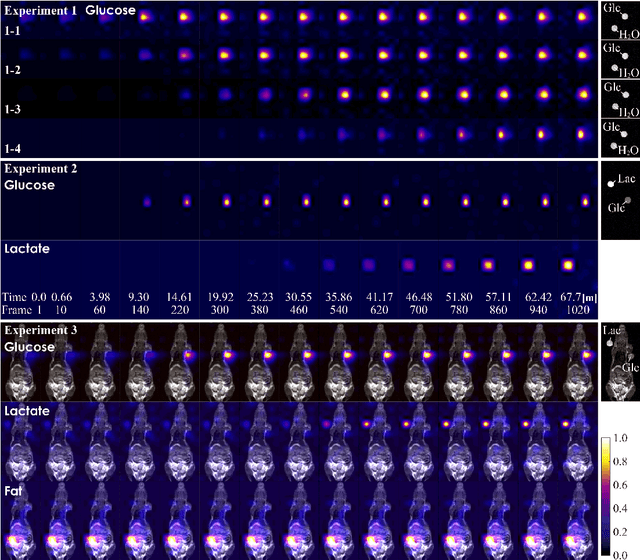
The objective of our study is to observe dynamics of multiple substances in vivo with high temporal resolution from multi-spectral magnetic resonance spectroscopic imaging (MRSI) data. The multi-spectral MRSI can effectively separate spectral peaks of multiple substances and is useful to measure spatial distributions of substances. However it is difficult to measure time-varying substance distributions directly by ordinary full sampling because the measurement requires a significantly long time. In this study, we propose a novel method to reconstruct the spatio-temporal distributions of substances from randomly undersampled multi-spectral MRSI data on the basis of compressed sensing (CS) and the partially separable function model with base spectra of substances. In our method, we have employed spatio-temporal sparsity and temporal smoothness of the substance distributions as prior knowledge to perform CS. The effectiveness of our method has been evaluated using phantom data sets of glass tubes filled with glucose or lactate solution in increasing amounts over time and animal data sets of a tumor-bearing mouse to observe the metabolic dynamics involved in the Warburg effect in vivo. The reconstructed results are consistent with the expected behaviors, showing that our method can reconstruct the spatio-temporal distribution of substances with a temporal resolution of four seconds which is extremely short time scale compared with that of full sampling. Since this method utilizes only prior knowledge naturally assumed for the spatio-temporal distributions of substances and is independent of the number of the spectral and spatial dimensions or the acquisition sequence of MRSI, it is expected to contribute to revealing the underlying substance dynamics in MRSI data already acquired or to be acquired in the future.

Kernel-based framework to estimate deformations of pneumothorax lung using relative position of anatomical landmarks

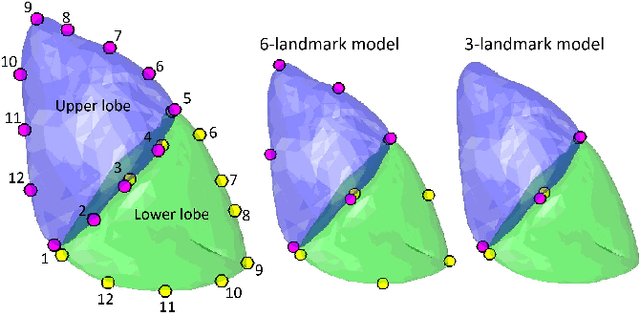
In video-assisted thoracoscopic surgeries, successful procedures of nodule resection are highly dependent on the precise estimation of lung deformation between the inflated lung in the computed tomography (CT) images during preoperative planning and the deflated lung in the treatment views during surgery. Lungs in the pneumothorax state during surgery have a large volume change from normal lungs, making it difficult to build a mechanical model. The purpose of this study is to develop a deformation estimation method of the 3D surface of a deflated lung from a few partial observations. To estimate deformations for a largely deformed lung, a kernel regression-based solution was introduced. The proposed method used a few landmarks to capture the partial deformation between the 3D surface mesh obtained from preoperative CT and the intraoperative anatomical positions. The deformation for each vertex of the entire mesh model was estimated per-vertex as a relative position from the landmarks. The landmarks were placed in the anatomical position of the lung's outer contour. The method was applied on nine datasets of the left lungs of live Beagle dogs. Contrast-enhanced CT images of the lungs were acquired. The proposed method achieved a local positional error of vertices of 2.74 mm, Hausdorff distance of 6.11 mm, and Dice similarity coefficient of 0.94. Moreover, the proposed method could estimate lung deformations from a small number of training cases and a small observation area. This study contributes to the data-driven modeling of pneumothorax deformation of the lung.

Deformation estimation of an elastic object by partial observation using a neural network

Deformation estimation of elastic object assuming an internal organ is important for the computer navigation of surgery. The aim of this study is to estimate the deformation of an entire three-dimensional elastic object using displacement information of very few observation points. A learning approach with a neural network was introduced to estimate the entire deformation of an object. We applied our method to two elastic objects; a rectangular parallelepiped model, and a human liver model reconstructed from computed tomography data. The average estimation error for the human liver model was 0.041 mm when the object was deformed up to 66.4 mm, from only around 3 % observations. These results indicate that the deformation of an entire elastic object can be estimated with an acceptable level of error from limited observations by applying a trained neural network to a new deformation.