On the phase diagram of extensive-rank symmetric matrix denoising beyond rotational invariance

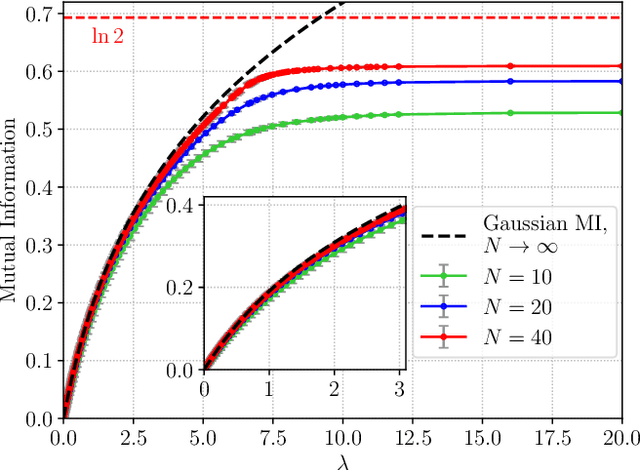
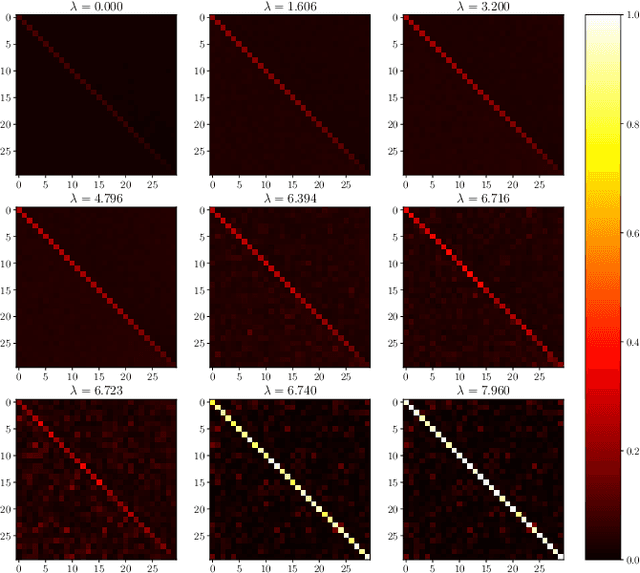
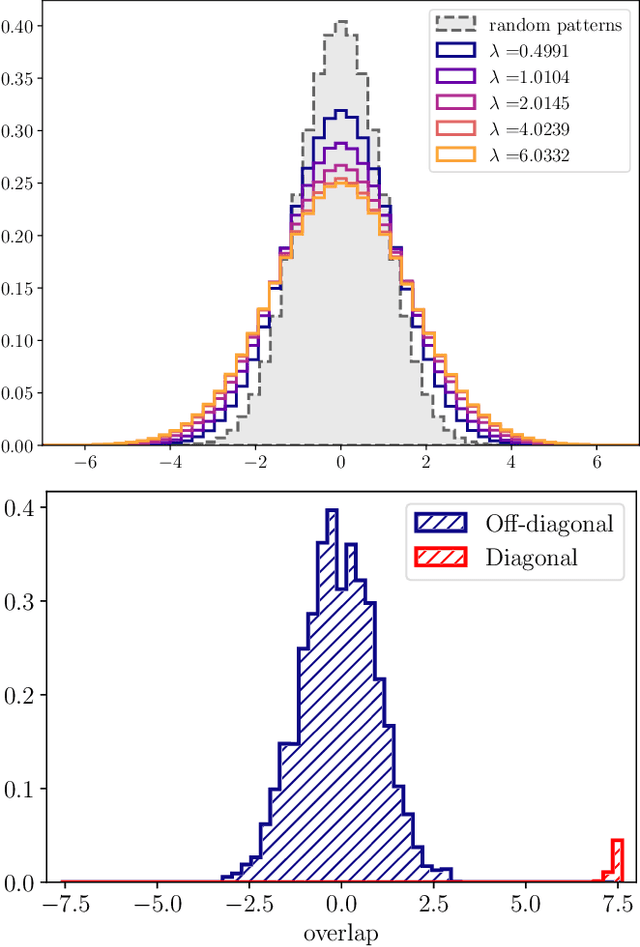
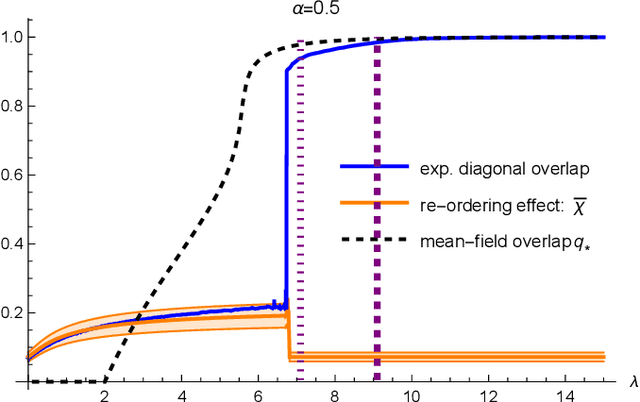
Matrix denoising is central to signal processing and machine learning. Its analysis when the matrix to infer has a factorised structure with a rank growing proportionally to its dimension remains a challenge, except when it is rotationally invariant. In this case the information theoretic limits and a Bayes-optimal denoising algorithm, called rotational invariant estimator [1,2], are known. Beyond this setting few results can be found. The reason is that the model is not a usual spin system because of the growing rank dimension, nor a matrix model due to the lack of rotation symmetry, but rather a hybrid between the two. In this paper we make progress towards the understanding of Bayesian matrix denoising when the hidden signal is a factored matrix $XX^\intercal$ that is not rotationally invariant. Monte Carlo simulations suggest the existence of a denoising-factorisation transition separating a phase where denoising using the rotational invariant estimator remains Bayes-optimal due to universality properties of the same nature as in random matrix theory, from one where universality breaks down and better denoising is possible by exploiting the signal's prior and factorised structure, though algorithmically hard. We also argue that it is only beyond the transition that factorisation, i.e., estimating $X$ itself, becomes possible up to sign and permutation ambiguities. On the theoretical side, we combine mean-field techniques in an interpretable multiscale fashion in order to access the minimum mean-square error and mutual information. Interestingly, our alternative method yields equations which can be reproduced using the replica approach of [3]. Using numerical insights, we then delimit the portion of the phase diagram where this mean-field theory is reliable, and correct it using universality when it is not. Our ansatz matches well the numerics when accounting for finite size effects.

Transfer Learning in $\ell_1$ Regularized Regression: Hyperparameter Selection Strategy based on Sharp Asymptotic Analysis

Transfer learning techniques aim to leverage information from multiple related datasets to enhance prediction quality against a target dataset. Such methods have been adopted in the context of high-dimensional sparse regression, and some Lasso-based algorithms have been invented: Trans-Lasso and Pretraining Lasso are such examples. These algorithms require the statistician to select hyperparameters that control the extent and type of information transfer from related datasets. However, selection strategies for these hyperparameters, as well as the impact of these choices on the algorithm's performance, have been largely unexplored. To address this, we conduct a thorough, precise study of the algorithm in a high-dimensional setting via an asymptotic analysis using the replica method. Our approach reveals a surprisingly simple behavior of the algorithm: Ignoring one of the two types of information transferred to the fine-tuning stage has little effect on generalization performance, implying that efforts for hyperparameter selection can be significantly reduced. Our theoretical findings are also empirically supported by real-world applications on the IMDb dataset.

Asymptotic Dynamics of Alternating Minimization for Non-Convex Optimization

This study investigates the asymptotic dynamics of alternating minimization applied to optimize a bilinear non-convex function with normally distributed covariates. We employ the replica method from statistical physics in a multi-step approach to precisely trace the algorithm's evolution. Our findings indicate that the dynamics can be described effectively by a two--dimensional discrete stochastic process, where each step depends on all previous time steps, revealing a memory dependency in the procedure. The theoretical framework developed in this work is broadly applicable for the analysis of various iterative algorithms, extending beyond the scope of alternating minimization.

Average case analysis of Lasso under ultra-sparse conditions

We analyze the performance of the least absolute shrinkage and selection operator (Lasso) for the linear model when the number of regressors $N$ grows larger keeping the true support size $d$ finite, i.e., the ultra-sparse case. The result is based on a novel treatment of the non-rigorous replica method in statistical physics, which has been applied only to problem settings where $N$ ,$d$ and the number of observations $M$ tend to infinity at the same rate. Our analysis makes it possible to assess the average performance of Lasso with Gaussian sensing matrices without assumptions on the scaling of $N$ and $M$, the noise distribution, and the profile of the true signal. Under mild conditions on the noise distribution, the analysis also offers a lower bound on the sample complexity necessary for partial and perfect support recovery when $M$ diverges as $M = O(\log N)$. The obtained bound for perfect support recovery is a generalization of that given in previous literature, which only considers the case of Gaussian noise and diverging $d$. Extensive numerical experiments strongly support our analysis.

Matrix completion based on Gaussian belief propagation

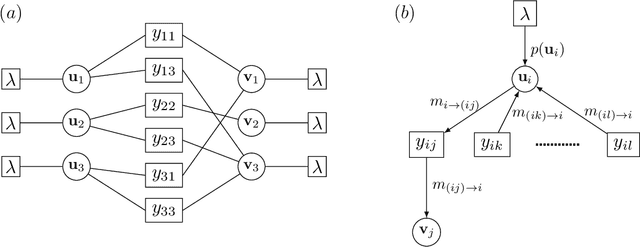
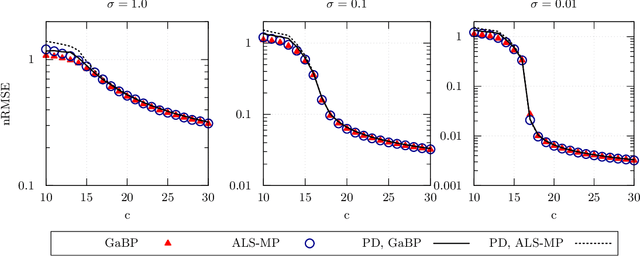
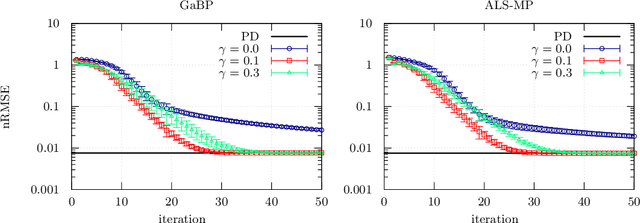
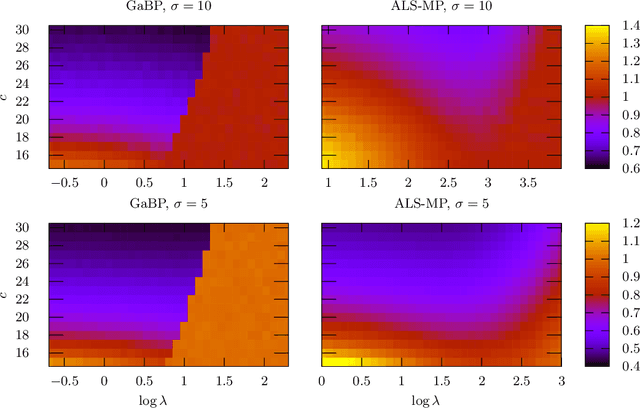
We develop a message-passing algorithm for noisy matrix completion problems based on matrix factorization. The algorithm is derived by approximating message distributions of belief propagation with Gaussian distributions that share the same first and second moments. We also derive a memory-friendly version of the proposed algorithm by applying a perturbation treatment commonly used in the literature of approximate message passing. In addition, a damping technique, which is demonstrated to be crucial for optimal performance, is introduced without computational strain, and the relationship to the message-passing version of alternating least squares, a method reported to be optimal in certain settings, is discussed. Experiments on synthetic datasets show that while the proposed algorithm quantitatively exhibits almost the same performance under settings where the earlier algorithm is optimal, it is advantageous when the observed datasets are corrupted by non-Gaussian noise. Experiments on real-world datasets also emphasize the performance differences between the two algorithms.